KöMaL Problems in Informatics, March 2012
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'I'Deadline expired on April 10, 2012. |
I. 289. Dominoes are fun to play with. Each piece contains two nonnegative integers and the corresponding number of dots. We say that a domino set is an \(\displaystyle N\)-set (\(\displaystyle 0\le N\le 10\)), if these integers fall between 0 and \(\displaystyle N\). Two domino pieces are considered to be identical if the pairs of numbers on them (sorted into ascending order) are the same. A set of dominoes does not contain identical dominoes.
For example, a 2-set contains the following pieces: [0 0] [0 1] [0 2] [1 1] [1 2] [2 2].
Your first task is to create the elements of an \(\displaystyle N\)-set by using a functional algorithm. The input of the function creating the set is the value of \(\displaystyle N\), while the output is the ordered sequence of the dominoes, as in the example. (``Példa'' is example, ``dominó'' is domino, and ``Eredmény'' is the result.)
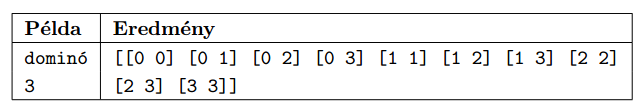
Your second task is to create a function that gives the total number of dots of an \(\displaystyle N\)-set. (``Pöttyszám'' is number of dots.)

In a family some children have domino sets, but they are mixed up during the play. Your third task is to select those pieces which occur more than once. The input of your function is the unsorted list of dominoes, while the output is the ordered list similar to the example. (``Többször'' is more than once.)
We recommend using Imagine Logo as a programming environment, but you can solve the task by using programming languages following the von Neumann model (such as C, C++, Pascal, ...). During your solution, apart from the inputs and outputs, you should use only the functional aspects of the programming language. Do not use variables. Repetition should be accomplished through recursion only. Try and decompose your solution into as many parametrizable functions as possible. You can read more about functional programming in problem I. 259.
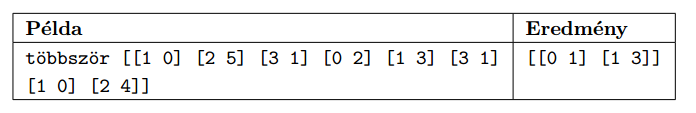
Your source code (i289.imp Imagine Logo Project, i289.pas, i289.cpp, ...) and a text file i289.txt -- describing your functions and giving the name of the developer environment to use for compiling -- should be submitted in a compressed file i289.zip.
(10 pont)
solution (in Hungarian), statistics
I. 290. Besides offering credit and managing deposits, banks also change and register various currencies. Fluctuating exchange rates strongly determine the commerce and economy of a country. In this task you are going to analyze some foreign exchange rates during the last two months of the last year by using data from the bank OTP. Exchange rates are updated during workdays, but this is complicated by the holidays and long weekends. Exchange rates on rest days are the same as the ones during the last working day before the rest day: exchange rates on October 28 are present in the table because the first day of November was a rest day.
Actual data are found in the tabulator separated UTF-8 encoded text file deviza.txt downloadable from our site.
Whenever possible, your solution should use formulae, functions and links. Auxiliary computations can be performed to the right of column V and below row 56.
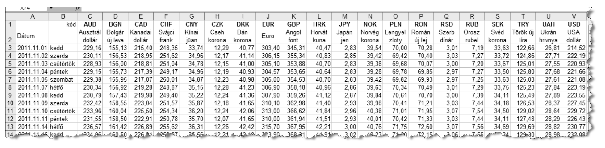
[1.] Open the file deviza.txt in a spreadsheet application such that the first piece of data is put into cell A1. Save the sheet named i290 in the default file format of the application. The first two columns of the sheet contain the date and day of the week, the first row contains the currency codes, while the second row the currency names. Further rows contain the middle prices of the corresponding foreign currencies. For example, the value 348,58 (with comma denoting the decimal mark) in cell K28 means that on December 5, 2011 one GBP was equal to 348,58 HUF.
[2.] Range C47:V47 should contain the ratio between the highest and lowest value of the actual currency.
[3.] Range C48:V48 should contain the number of days during which the actual exchange rate was higher than its average. Rest days should be taken into account when counting days and computing the average.
[4.] On November 3, an investor bought (on middle prices) AUD, CAD and USD for 1 million HUF each. On December 19, the investor sold all the three types of dollars. The investor was charged 0.5% for the transactions. (In reality, banks use buying the selling rates when exchanging money, and the difference of these two is the profit of the bank. But for simplicity, we now use only middle prices and some additional charges.) Cell G54 should contain the profit of the investor. The format of the cell should be set to HUF currency without decimal digits.
[5.] Cell G55 should contain the number of currencies which attained their highest value on the last working day of the year (December 30, 2011).
[6.] You should create an expression in cell C52 which computes the actual exchange rate based on the values of cells C51 and C50, or displays an ``Invalid data'' message, if the corresponding data is missing (either the date is out of range or the currency is not in our list). For example, if 2011.11.17 is entered into cell C50 and NOK entered into cell C51, then cell C52 should display 39,39. If any of the two cells above is empty, cell C52 should remain empty, too. You should pay attention however, for example, for December 12, 2011 the valid exchange rate is known even if the original table does not contain it.

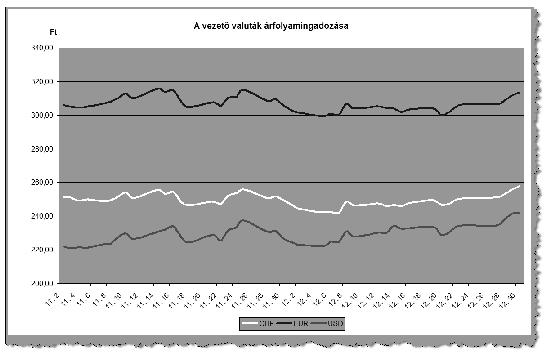
[7.] You should create a graph showing the fluctuating exchange rates for the USD, CHF and EUR during the whole period. You should consider the following.
\(\displaystyle a)\) The graph should show only data corresponding to working days.
\(\displaystyle b)\) The type of the graph should be line diagram.
\(\displaystyle c)\) The diagram should be created on a new sheet.
\(\displaystyle d)\) The rates for the USD should be displayed in thick red, the EUR in thick blue, while the CHF in thick white. The background and the legend should be dark enough so that the white curve is also properly visible.
\(\displaystyle e)\) The legend should be displayed below the diagram.
\(\displaystyle f)\) The title should be ``Fluctuations of the leading foreign currencies''.
\(\displaystyle g)\) The date should not contain the year. The scale on the vertical axis should range from 200 to 340, and Ft (that is, HUF) should be displayed on the top of that axis.
On the original sheet currency codes should be in bold face. These and the currency names should be centered in both directions. If necessary, the names can occupy more rows, according to the example. Range A1:B2 should be displayed as in the example.
[8.] Background color for cells with computed values should be pale green with dark green border.
Your spreadsheet (i290.xls, i290.ods, ...) together with a short documentation (i290.txt, i290.pdf, ...) should be submitted, also containing the name and version number of the spreadsheet application.
(10 pont)
solution (in Hungarian), statistics
I. 291. In this task you will consider the following (well-known) interesting simple mathematical game.
[] The game contains some transparent Plexiglas squares with different geometric shapes painted on them. One card contains one color and the painting is not transparent.
[] During the play these cards should be stacked on top of each other in a rack having the same size as the cards. During the stacking, shapes on the cards will (partially) hide one another, hence one can create interesting figures. (A painted card without symmetry can be placed in 8 ways in the rack.)
[] A puzzle book contains the possible figures.
You should create your own cards for this game by using 2 or 3 colors.
You should also write documentation for the game, containing the rules of the game and pictures of the cards, further, 10 puzzles to solve. Each puzzle should be solvable by using at most 4 cards. Solutions to the puzzles should be on the last page.
You should also create a short presentation illustrating the essential features of the game and showing a solution of a puzzle.
A compressed i291.zip file containing your documentation (i291.pdf) and presentation (i291.ppt, i291.odp, ...) should be submitted.
(10 pont)
 |
Problems with sign 'S'Deadline expired on April 10, 2012. |
S. 70. Adam moved to Nameless City and immediately drew a precise map to grasp every detail: he recorded the length of each street on his map in micrometers. Of course, he is also a very careful route planner: he now wants to get from A to B by minimizing the difference between the lengths of the longest and shortest streets on his route. Your program should determine such a route for Adam.
Your program reads the description of the city from the standard input. The first line of the input contains the number of road crossings N and (after a space separator) the number of streets M connecting them (1 N
N 1000, 0
1000, 0 M
M 5000). The second line of the input identifies crossings A and B by giving their numbers. Then each of the following M lines describes a street in a form XiYiLi, where Xi and Yi are the numbers of the crossings connected by street i,finally Li denotes the length of street i (1
5000). The second line of the input identifies crossings A and B by giving their numbers. Then each of the following M lines describes a street in a form XiYiLi, where Xi and Yi are the numbers of the crossings connected by street i,finally Li denotes the length of street i (1 Li
Li 109). Assume that the two endpoints of a street are always disjoint, further, there are no two streets having both endpoints in common. Crossings are numbered from 0 to N-1.
109). Assume that the two endpoints of a street are always disjoint, further, there are no two streets having both endpoints in common. Crossings are numbered from 0 to N-1.
The single line on the standard output should contain a single number: the minimal attainable difference, if A is connected with B, and -1 otherwise.
In the example, Példa bemenetek are sample inputs, while Példa kimenetek are the corresponding outputs.
In order to obtain the maximal number of points, your code should handle our largest test cases within 1 second.
The source code of your program (s70.pas, s70.cpp, ...) -- without the .exe or any other auxiliary files generated by the compiler -- should be submitted in a compressed file s70.zip, also containing a brief description of your solution (s70.txt, s70.pdf, ...) and the name of the developer environment to use for compiling.

(10 pont)
$Var(Body)
Upload your solutions above
