A KöMaL 2012. márciusi matematika feladatai

Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.

Feladat típusok elrejtése/megmutatása:

K-jelű feladatok

A beküldési határidő 2012. április 10-én LEJÁRT.

K. 331. Egy autónak egy sivatagos részen kell átkelnie, 600 km-t kell megtennie. Az autó 400 km-re elegendő üzemanyagot tud magával vinni a benzintartályában, más módon üzemanyagot nem tud szállítani. Az autó 50--60 km/h közötti átlagsebességgel tud haladni, és feltétel, hogy reggel 8-kor indulva este 8 órára már a túlsó oldalon legyen. Legkevesebb hány ilyen autót kell a sivatag egyik oldaláról indítani, hogy közülük egy átjusson a sivatagon, és a többi térjen vissza? Egyik autóból a másikba való áttankolás lehetséges.

(6 pont)

megoldás, statisztika

K. 332. Vegyünk néhány pozitív egész számot, melyek összege 20. Szorozzuk össze őket, így kapjuk az X számot. Mennyi X maximális értéke?

(6 pont)

megoldás, statisztika

K. 333. Egy háromszög három belső, majd a három külső szögét megfelelő sorrendben leírva egy növekvő számtani sorozat hat egymást követő tagját kapjuk. Hány fokosak a háromszög szögei? (A számtani sorozatban az egymást követő tagok különbsége állandó, azaz a sorozat tagjai egyenletesen növekszenek.)

(6 pont)

megoldás, statisztika

K. 334. Alma lelépte, majd táblázatba foglalta a kertjükben lévő gyümölcsfák távolságát (lépésben mérve):

	Almafa	Körtefa	Diófa
Mandulafa	5	12	35
Almafa	0	13	40

Hány lépés távolságra van a diófától a körtefa?

(6 pont)

megoldás, statisztika

K. 335. Egy különleges számológépen csak négy gomb van: 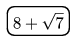(nyolc plusz gyök hét), (összeadás), 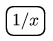(reciprok) és (egyenlő).

A számológép mindig pontos értékkel számol, és az éppen aktuális értéket a dupla lenyomásakor konstansként tárolni is tudja, azaz ezután az nyomásakor ezzel az értékkel növeli a számot akárhányszor (pl. 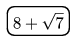lenyomása után ezt látjuk: $24+3\sqrt 7$ ). Bizonyítsuk be, hogy a

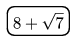
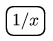
... (56-szor)

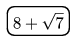
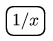
... (15-ször)

műveletsor eredménye 1.

(6 pont)

megoldás, statisztika

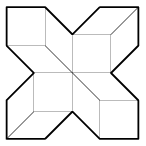
K. 336. Az ábrán látható konkáv 16-szöget négy egybevágó négyzetre és nyolc egybevágó rombuszra vágtuk, a rombuszok kisebbik szöge 45 fokos. Mekkora a 16-szög területe, ha a rombuszok hosszabb átlója 10,7 cm-es?

(6 pont)

megoldás, statisztika

C-jelű feladatok

A beküldési határidő 2012. április 10-én LEJÁRT.

C. 1115. Mutassuk meg, hogy minden n természetes szám esetén az

n²(n²-1)(n²-n-2)

osztható 48-cal.

(5 pont)

megoldás, statisztika

C. 1116. Egy konvex négyszög minden oldalát osszuk fel nyolc egyenlő részre, majd minden osztópontot kössünk össze az ábra szerint a vele szemközti oldalon levő megfelelő osztóponttal. Az így kapott kis négyszögeket színezzük be sakktáblaszerűen fekete és fehér színűre. Igazoljuk, hogy a fekete négyszögek területének összege megegyezik a fehér négyszögek területének összegével.

(5 pont)

megoldás, statisztika

C. 1117. Egy négyzetrácsos papírra olyan rácstéglalapot (oldalai rácsegyenesek) rajzoltunk, amely n darab kis rácsnégyzetből áll. Igazoljuk, hogy ha a téglalap belsejébe eső rácspontok számához hozzáadjuk a határvonalán található rácspontok számának felét, majd az így kapott számból 1-et elveszünk, akkor n-t kapunk.

(5 pont)

megoldás, statisztika

C. 1118. Oldjuk meg a

$4x^2 + \frac34 = 2\sqrt x$

egyenletet a valós számok halmazán.

(5 pont)

megoldás, statisztika

C. 1119. Az ábrán látható módon a rövidebb, 10 cm hosszú befogójuk mentén egymáshoz rögzítettünk két egyforma (30-60 fokos) derékszögű vonalzót, majd az alakzat tetejére tettünk egy egyenlő szárú derékszögűt is. Elférne-e az így kapott tetraéder belsejében egy 3,2 cm sugarú teniszlabda?

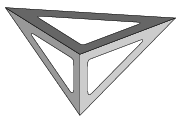
(5 pont)

megoldás, statisztika

B-jelű feladatok

A beküldési határidő 2012. április 10-én LEJÁRT.

B. 4432. A számítógép képernyőjén egy 98×98-as sakktábla látható, a szokásos módon színezve. Az egér segítségével kijelölhetünk tetszőleges olyan téglalapot, amelyet a sakktábla vonalai határolnak, majd rákattintva az ebben a téglalapban lévő mezők színe ellenkezőjére változik. Minimálisan hány kattintás szükséges ahhoz, hogy a sakktábla teljesen egyszínű legyen?

(5 pont)

megoldás, statisztika

B. 4433. Oldjuk meg az (1+x)⁸+(1+x²)⁴=82x⁴ egyenletet.

(3 pont)

megoldás, statisztika

B. 4434. Bizonyítsuk be, hogy minden 10-zel nem osztható természetes számhoz található olyan természetes szám, hogy szorzatuk 10-es számrendszerben felírva palindrom szám legyen.

(4 pont)

megoldás, statisztika

B. 4435. A hegyesszögű ABC háromszög A csúcsból induló magasságának talppontja T, BC oldalának felezőpontja F. Az AB és AC oldalakra kifelé írt négyzetek középpontja pedig K, illetve L. Igazoljuk, hogy KTFL húrnégyszög.

Javasolta: Miklós Szilárd (Herceghalom)

(4 pont)

megoldás, statisztika

B. 4436. Legyenek x, y, z olyan pozitív egész számok, amelyekre

$\frac{6841x-1}{9973}+\frac{9973y-1}{6841}=z.$

Igazoljuk, hogy

$\frac{x}{9973}+\frac{y}{6841}>1.$

Javasolta: Mészáros József (Jóka)

(4 pont)

megoldás, statisztika

B. 4437. Szerkesszünk háromszöget, ha adott köré írt körének és valamelyik két hozzáírt körének a középpontja.

(4 pont)

megoldás, statisztika

B. 4438. Az ABC háromszög szögfelezői a szemközti oldalt rendre az A₁, B₁ és C₁ pontokban metszik. Milyen háromszögek esetén lesz

$\overrightarrow{AA_1} + \overrightarrow{BB_1}+ \overrightarrow{CC_1} =\mathbf{0}?$

(Matlap, Kolozsvár)

(3 pont)

megoldás, statisztika

B. 4439. A sík egymástól különböző B és C pontjaihoz határozzuk meg azon A pontok mértani helyét, amelyekre az ABC háromszög A-hoz tartozó magassága mértani közepe a BC+AC és BC-AC szakaszoknak.

(3 pont)

megoldás, statisztika

B. 4440. Egy téli napon a szórakozott matematikus egy hosszú egyenes sétányon sétáltatta öreg tacskóját. Annyira elmélyedt a gondolataiban, hogy egyszer csak azt vette észre, hogy a kutya nincs mellette. A hóesés miatt a látótávolság csak 5 méter, a matematikus se maga előtt, se maga mögött nem látja kutyáját, és azt sem tudja, melyik irányba szökhetett el. Rövid töprengés után elindult, hogy megkeresse tacskóját. A kutya legfeljebb fele akkora sebességgel képes haladni, mint gazdája. A matematikus olyan keresési stratégiát választott, hogy a lehető legkisebb c konstans mellett teljesüljön az a feltétel, hogy ha a kutyája tőle x távolságra van, akkor legfeljebb cx hosszúságú utat kelljen megtennie, hogy megtalálja. Mi ez a c érték?

(5 pont)

megoldás, statisztika

B. 4441. Egy tetraéder oldallapjainak a területe a, b, c, d. Az a és b területű lapok közötti szög $\gamma$ , a b és c közötti szög $\alpha$ , a c és a közötti szög pedig $\beta$ . Igazoljuk, hogy

d²=a²+b²+c²-2ab^.cos $\gamma$ -2bc^.cos $\alpha$ -2ca^.cos $\beta$ .

(5 pont)

megoldás, statisztika

A-jelű feladatok

A beküldési határidő 2012. április 10-én LEJÁRT.

A. 557. Mutassuk meg, hogy a pozitív egészek kiszínezhetők három színnel úgy, hogy az x+y=z² egyenletnek ne legyen különböző, azonos színű számokból álló (x,y,z) megoldása.

Kolmogorov kupa, 2011; F. Petrov és I. Bogdanov feladata

(5 pont)

statisztika

A. 558. Bizonyítsuk be, hogy van olyan C>0 konstans, amire a következő állítás teljesül: Ha n pozitív egész, és $A_1,A_2,\ldots,A_N\subset\{1,2,\ldots,n\}$ olyan halmazok, amelyek közül bármely kettőnek legalább két, továbbá bármely háromnak legfeljebb három közös eleme van, akkor N<Cn².

Javasolta: Gyenes Zoltán (Budapest)

(5 pont)

statisztika

A. 559. Az ABC háromszög beírt köre k. A k_A kör k-t, az AB, illetve az AC oldalt rendre az A', A_B, illetve az A_C pontban érinti. Hasonlóan definiáljuk a k_B és k_C köröket, továbbá a B' és C' pontokat. Az A'B'A_B és A'C'A_C körök A'-től különböző metszéspontja K. Az A'K egyenes és k A'-től különböző metszéspontja R. Igazoljuk, hogy R a k_B és a k_C körök hatványvonalán van.

Kolmogorov kupa, 2011; F. Ivlev feladata

(5 pont)

statisztika

A matematika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:

megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.

(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

Már regisztráltál?
Új vendég vagy?