KöMaL Problems in Mathematics, October 2012
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on November 12, 2012. |
K. 343. A box contains buttons, with four holes, two holes or one hole on them. There is at least one button of each kind, and there are 61 holes and 27 buttons altogether. Given that the number of buttons with one hole is the largest, find the possible numbers of the individual types of buttons.

(6 pont)
solution (in Hungarian), statistics
K. 344. In a fun fair, adults and children are charged the same amount for a ride on the carousel, and the first few rides are for free. However, the number of free rides is greater for children. Two adults with one child paid 3200 forints (HUF) for 20 rides, three adults with two children only paid 2600 forints for the same number of rides, and two adults with three children paid 2400. What is the number of free rides for children and for adults, if everyone used up all their free rides?
(6 pont)
solution (in Hungarian), statistics
K. 345. A total of 90 cm length of wire is used to make two pieces of the square frame with a handle that is illustrated in the figure. The length of the handle in cm is an integer, and it equals the length of the side of the square. The total area of the two frames is 170cm2. Find the difference between the heights of the two frames. (The height is measured from the bottom of the handle to the top of the square.)

(6 pont)
solution (in Hungarian), statistics
K. 346. From the third term onwards, the terms of a sequence are obtained by subtracting from the previous term the term preceding that. (Thus the third term = the second term - the first term, the fourth term = the third term - the second term, and so on.) The first term is 2, the sum of the first 2012 terms is 2012. What is the second term?
(6 pont)
solution (in Hungarian), statistics
K. 347. Grandma in her seventies has more sons than daughters. Each of her sons has as many sons as siblings. Each of her daughters has daughters only. How old is grandma if the half of her age in years equals the sum of the numbers of her sons and grandsons?
(6 pont)
solution (in Hungarian), statistics
K. 348. The numerator and denominator of a fraction are two-digit numbers. The digit 3 occurs in the numerator, 5 occurs in the denominator. The other two digits are equal. How many such fractions of different values are there?
(6 pont)
 |
Problems with sign 'C'Deadline expired on November 12, 2012. |
C. 1135. Six students qualified for the finals of the mathematics competition organized by a school: Alan (A), Bill (B), Cecilia (C), Diana (D), Eleanor (E) and Frank (F). When the first problem had been assessed, they were told that 3 students achieved 10 points and the others achieved 7. Everyone was instructed to guess who had the 10 points. The guesses were as follows: A, B, D; A, C, E; A, D, E; B, C, E; B, D, E; C, D, E. Three of them each guessed two right, two of them each guessed one right, and one had no right guess. It turned out that no one guessed all three right. Which students got 10 points?
(5 pont)
solution (in Hungarian), statistics
C. 1136. M is the orthocentre of triangle ABC, F is the midpoint of side AB, and T is the foot of the altitude drawn from vertex A. Given that MF=4, TM=5, TF=6, construct the triangle ABC.
(5 pont)
solution (in Hungarian), statistics
C. 1137. The first two terms of the Fibonacci sequence are a1=1, a2=1, and every further term equals the sum of the two preceding terms, that is, an=an-2+an-1 (n 3). Prove that the sequence has no term that leaves a remainder of 4 when divided by 13.
3). Prove that the sequence has no term that leaves a remainder of 4 when divided by 13.
(5 pont)
solution (in Hungarian), statistics
C. 1138. Solve the following equation on the set of real numbers: .
(5 pont)
solution (in Hungarian), statistics
C. 1139. What is the minimum possible length of the hypotenuse of a right-angled triangle whose perimeter is k?
(5 pont)
 |
Problems with sign 'B'Deadline expired on November 12, 2012. |
B. 4472. Prove that the sum of the squares of seven consecutive integers cannot be a perfect square.
(3 pont)
solution (in Hungarian), statistics
B. 4473. Consider the cubic equation px3-qx2-rx+s=0 where p, q, r, s are positive numbers such that ps=qr. Prove that the equation has two different real roots. On what condition are there three different roots?
(3 pont)
solution (in Hungarian), statistics
B. 4474. The points K, L, M and N, respectively, lie on sides AB, BC, CD and DA of a square ABCD. Given that  KLA=
KLA= LAM=
LAM= AMN=45o, prove that KL2+AM2=LA2+MN2.
AMN=45o, prove that KL2+AM2=LA2+MN2.
(4 pont)
solution (in Hungarian), statistics
B. 4475. Prove that for every convex polyhedron with five faces there exists a plane that does not pass through any vertex but intersects each face.
Suggested by V. Vígh, Szeged
(5 pont)
solution (in Hungarian), statistics
B. 4476. Prove that there are infinitely many ways to express 169 as a sum of the squares of two rational numbers.
(4 pont)
solution (in Hungarian), statistics
B. 4477. In an acute triangle ABC,  <
< (with conventional notations). Let R and P be the feet of the altitudes drawn from vertices A and C, respectively. Let Q denote a point of line AB, different from P, such that AP.BQ=AQ.BP. Prove that line RB bisects the angle PRQ.
(with conventional notations). Let R and P be the feet of the altitudes drawn from vertices A and C, respectively. Let Q denote a point of line AB, different from P, such that AP.BQ=AQ.BP. Prove that line RB bisects the angle PRQ.
Suggested by J. Mészáros, Jóka
(5 pont)
solution (in Hungarian), statistics
B. 4478. Prove that if  ,
,  and
and 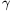 are the angles of an acute-angled triangle then
are the angles of an acute-angled triangle then .
(4 pont)
solution (in Hungarian), statistics
B. 4479. In an isosceles triangle ABC, D and E denote points on the legs AB and AC, respectively, such that AD=BC=EC. What may be the measure of the angle at vertex A if triangle ADE is isosceles?
(6 pont)
solution (in Hungarian), statistics
B. 4480. The escribed circle drawn to side AB of a triangle ABC touches the lines of sides AB, BC and CA at the points E, F, G, respectively. The intersection of lines AF and BG is H. The inscribed circle of the triangle formed by the midlines of triangle ABC touches the side parallel to AB at point N. Prove that the points E, H and N are collinear.
Suggested by Sz. Miklós, Herceghalom
(5 pont)
solution (in Hungarian), statistics
B. 4481. Find all polynomials f of integer coefficients such that for every positive integer n the prime factors of the numbers n and f(n) coincide.
(5 pont)
 |
Problems with sign 'A'Deadline expired on November 12, 2012. |
A. 569. Call a set interesting if 2y-x
 A for all pairs x,y
A for all pairs x,y A with x<y. Let a1<a2<...<ak be positive integers (k
A with x<y. Let a1<a2<...<ak be positive integers (k 2) whose greatest common divisor is 1. Prove that if A is an interesting set and
2) whose greatest common divisor is 1. Prove that if A is an interesting set and then a1+ak-3
 A.
A.
Proposed by: Carlos Gustavo T. A. Moreira (Gugu), Rio de Janeiro
(5 pont)
A. 570. Given a triangle ABC. For an arbitrary interior point X of the triangle denote by A1(X) the point intersection of the lines AX and BC, denote by B1(X) the point intersection of the lines BX and CA, and denote by C1(X) the point intersection of the lines CX and AB. Construct such a point P in the interior of the triangle for which each of the quadrilaterals AC1(P)PB1(P), BA1(P)PC1(P) and CB1(P)PA1(P) has an inscribed circle.
Proposed by: G. Holló, Budapest
(5 pont)
A. 571. The side lengths of a triangle are a, b, and c. Prove that
Proposed by: Daniel Campos, San Jose, Costa Rica
(5 pont)
Upload your solutions above.
