KöMaL Problems in Mathematics, December 2012
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on January 10, 2013. |
K. 355. Let F be the point lying closer to point A that divides side AB of a square ABCD in a 1:2 ratio. Let E be the point closer to D that divides side AD in a 1:2 ratio, and let G be the point closer to C that divides side CD in a 1:5 ratio. In what ratio do the diagonals of quadrilateral EFBG divide each other?
(6 pont)
solution (in Hungarian), statistics
K. 356. Two digits of the six-digit number 2_01_2 are missing. What digits may be written in the vacant places, so that the resulting six-digit number is divisible by 36 and also by 117?
(6 pont)
solution (in Hungarian), statistics
K. 357. Find all primes between 1 and 100 that are 1 greater than a multiple of 4 and 1 smaller than a multiple of 5.
(6 pont)
solution (in Hungarian), statistics
K. 358. In a warehouse, there are cubical boxes of the same mass and size stacked in the form of a large rectangular block. A worker is loading the boxes onto a truck. In each step, he transfers to the truck one vertical or horizontal layer of boxes, with a thickness of a single box. (He is able to approach the stack of boxes from any direction.) The mass of the boxes is a whole number of kilograms. The total mass of the boxes loaded in the first step is 60 kg, in the second step it is 84 kg, and in the third step it is 112 kg. What may be the total mass of all the boxes, in kilograms?
(6 pont)
solution (in Hungarian), statistics
K. 359. Let the natural number n be at least 5. Prove that it is possible to divide a rectangle into n smaller rectangles, such that no two adjacent small rectangles form a larger rectangle together.
Based on a problem of the Bolyai Competition, 2012
(6 pont)
solution (in Hungarian), statistics
K. 360. The accompanying figure is drawn on a square lattice. The separation of consecutive parallel grid lines is 5 mm. The polygon consists of 999 line segments. Determine its length, rounded to the nearest metre.
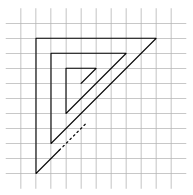
(6 pont)
 |
Problems with sign 'C'Deadline expired on January 10, 2013. |
C. 1145. Prove that odd numbers and the multiples of 4 can all be expressed as differences of two perfect squares, whereas the even numbers not divisible by 4 cannot.
(5 pont)
solution (in Hungarian), statistics
C. 1146. Given one vertex and the midpoints of all the sides of a pentagon on the plane, prove that it is always possible to find a point on the plane, such that it forms a parallelogram with three of the six given points, and another parallelogram with the other three points.
(5 pont)
solution (in Hungarian), statistics
C. 1147. Solve the equation .
(5 pont)
solution (in Hungarian), statistics
C. 1148. The diagonals of a quadrilateral inscribed in a circle are perpendicular. Prove that the distance of any side from the centre of the circle is equal to the half of the opposite side.
Kvant
(5 pont)
solution (in Hungarian), statistics
C. 1149. The number of one-element subsets, the number of two-element subsets and the number of three-element subsets of a set of more than three elements are consecutive terms of an arithmetic progression. How many elements does the set have?
(5 pont)
 |
Problems with sign 'B'Deadline expired on January 10, 2013. |
B. 4492. Prove that if the natural numbers a and b only differ in the order of their digits then the sum of the digits in the numbers 5a and 5b is the same.
Kvant
(3 pont)
solution (in Hungarian), statistics
B. 4493. Let (n,k) denote the greatest common divisor of the positive integers n and k, and let [n,k] denote their least common multiple. Show that, for all positive integers a, b, c, the greatest common divisor of the numbers [a,b], [b,c], [c,a] equals the least common multiple of the numbers (a,b), (b,c), (c,a).
(4 pont)
solution (in Hungarian), statistics
B. 4494. F is the midpoint of base BC of the isosceles triangle ABC. D is an interior point of the line segment BF. The perpendicular dropped from point D onto BC intersects side AB at M, and the line through point D, parallel to AB intersects side AC at P. Express the ratio of the areas of triangles AMP and ABC in terms of k=BD:BC.
Matlap, Cluj-Napoca - Kolozsvár, Romania
(3 pont)
solution (in Hungarian), statistics
B. 4495. Given the parallelogram ABCD and points F and G, such that AF=FC, BG=GD and given that triangles AFC and BGD are similar, prove that the line FG is perpendicular to a side of the parallelogram.
Suggested by Sz. Miklós, Herceghalom
(5 pont)
solution (in Hungarian), statistics
B. 4496. An absent minded professor is travelling in a train along a subway line having infinite length in both directions. He would like to get from Alpha station to Tau station. At every station, the probability that he looks up from his notes is the same p>0 (independently of each other). If he looks up and observes that he has reached his destination, then he gets off. If he can see that he has passed his destination, then he also gets off and gets on the train travelling in the opposite direction. If he looks up and sees that he has not reached his destination yet, he stays in his train. If he does not look up, he will stay on the train wherever he is. What is the probability that he will get off at Tau station after a while?
(4 pont)
solution (in Hungarian), statistics
B. 4497. The sequence (an) is defined as follows: a1=a2=1, a3=2, (n
 1). Prove that all terms of the sequence are integers.
1). Prove that all terms of the sequence are integers.
(5 pont)
solution (in Hungarian), statistics
B. 4498. A vertex B of a convex quadrilateral ABCD is said to be ``special'' if the reflection of line BD in the bisector of angle ABC bisects the diagonal AC. Prove that if one vertex of a cyclic quadrilateral is special then all vertices are special.
Suggested by P. Maga, Budapest
(5 pont)
solution (in Hungarian), statistics
B. 4499. Let P be an interior point of an acute-angled triangle A1A2A3. The points Ti are such that the line segment AiTi touches the circle of diameter PAi+1 at Ti (i=1,2,3, A4=A1). Show that .
Suggested by Á. Péter, Sepsiszentgyörgy (Matlap, Cluj-Napoca - Kolozsvár, Romania)
(4 pont)
solution (in Hungarian), statistics
B. 4500. Is there an at least second-degree polynomial of integer coefficients, such that the numbers n,f(n),f(f(n)),... are pairwise relative primes for all positive integers n?
(6 pont)
solution (in Hungarian), statistics
B. 4501. The height of a regular tetrahedron is 18 units. The tetrahedron is reflected in the midpoint of one of its altitudes. Find the volume and surface area of the common part of the two solids.
(5 pont)
 |
Problems with sign 'A'Deadline expired on January 10, 2013. |
A. 575. Prove that if and
, then it is possible to select at most four, not necessarily distinct elements from S, whose sum is a power of 2.
Proposed by: Sándor Kiss, Budapest
(5 pont)
A. 576. Find all positive integers n, nonzero reals and real t for which there exists a finite, nonempty set
of points in the plane S and a nonconstant function
such that
for every similarity transformation 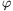 of the plane S.
of the plane S.
Proposed by: Tamás Ágoston, Budapest and Márton Mester, Cambridge
(5 pont)
solution (in Hungarian), statistics
A. 577. Prove that if the edges of a k-chromatic graph are colored with two colors then there is a tree in the graph, containing k vertices, whose edges have the same colors.
Miklós Schweitzer Competition, 2012
(5 pont)
Upload your solutions above.
