KöMaL Problems in Physics, January 2013
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'M'Deadline expired on February 11, 2013. |
M. 329. Discharge a pencil-sized battery (AA) or rechargeable battery of the same size through a resistor of constant resistance. Measure how much charge flow through the resistor, and how much energy is delivered by the battery.
(6 pont)
 |
Problems with sign 'P'Deadline expired on February 11, 2013. |
P. 4497. The length of a glass tube, which is closed at one end is  =100 cm. Holding it vertically with its closed end at its top, it is immersed into mercury to half of its height. What is the height of the mercury in the tube? The atmospheric pressure is H=75 Hgcm.
=100 cm. Holding it vertically with its closed end at its top, it is immersed into mercury to half of its height. What is the height of the mercury in the tube? The atmospheric pressure is H=75 Hgcm.
(3 pont)
solution (in Hungarian), statistics
P. 4498. A plano-convex and a plano-concave lens exactly fit to each other along their curved surfaces. The refractive index of the material they are made of is 1.5, and the focal length of the plano-convex lens is 40 cm.
a) What is the power of each lens?
b) What is the radius of the curved surfaces of the lenses?
(3 pont)
solution (in Hungarian), statistics
P. 4499. The mass of an empty balloon is measured with a sensible electronic scale. The mass is 3.7 g. After blowing the balloon the reading on the scale was 4.5 g. The ,,perimeter'' of the balloon, whose shape could well be approximated as a sphere, was measured as 73 cm.
a) How much air was blown into the balloon?
b) What is the excess pressure inside the balloon, if the temperature in the room is 25 oC?
c) What is the drag force exerted on the balloon, when it descends uniformly?
(4 pont)
solution (in Hungarian), statistics
P. 4500. A small bead can slide from A to B along the paths shown in the figure. The paths are circular arcs lying in a vertical plane, and they are symmetrical about the straight line through the points A and B. The angle between the straight line and the horizontal is 45o.
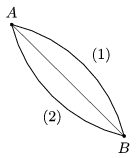
a) Along which path will the bead reach point B in a shorter time, and what can we state about the final speed in each case, if there is no friction?
b) What can be stated about the final speeds if friction is not negligible, and the coefficient of friction is the same in both paths?
(4 pont)
solution (in Hungarian), statistics
P. 4501. A fixed U shaped small narrow tube is turned upside-down and a thread of length  is hanging in it as shown in the figure. Initially the length of the thread is
is hanging in it as shown in the figure. Initially the length of the thread is  /2 in each side. This is an unstable equilibrium since friction is negligibly small.
/2 in each side. This is an unstable equilibrium since friction is negligibly small.
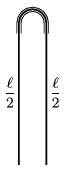
a) If the thread begins to slide to one side what will its speed be when it is straight?
b) What will the speed of the thread be when its momentary centre of mass is just at the same level as that end of the thread which is moving up?
(4 pont)
solution (in Hungarian), statistics
P. 4502. A disc is given a push and slides on the top a horizontal table. It stops in a distance of L0. When the disc is placed to the rim of the table, which is at a height of H, and is given the same initial speed it reaches the ground at a distance of d from the table.
a) What is the kinetic frictional coefficient between the table and the disc?
b) At what distance from the table will the disc reach the ground if initially it is not exactly at the rim of the table but at a distance of L from the rim, (L<L0), the disc is given the same initial speed, and slides towards the rim of the table.
(Data: H=L0=d=0.8 m; L=0.6 m.)
(4 pont)
solution (in Hungarian), statistics
P. 4503. The pressure and the volume of a sample of 0.4 moles Helium gas is doubled. Initially its pressure was 105 Pa, and its volume was 10 dm3. Determine those quantities from the list below which can be given uniquely:
a) The work done on the gas;
b) The heat given to the gas;
c) The change in the energy of the gas.
(4 pont)
solution (in Hungarian), statistics
P. 4504. The n-storey symmetrical tower shown in the figure was built from dominoes of length 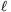 . How long are the balconies of the tower if each domino is pulled out as much as possible?
. How long are the balconies of the tower if each domino is pulled out as much as possible?
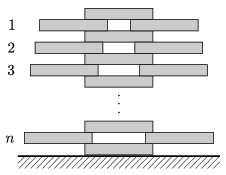
(5 pont)
solution (in Hungarian), statistics
P. 4505. The values the resistance of the resistors connected to the voltage supply of U=120 V, as shown in the figure are unknown. When the switch is closed the reading on the voltmeter changes by 16 V, and the power dissipated by the resistor R1 changes by 51.2 W.
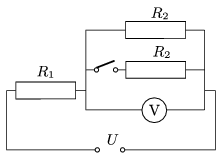
a) Using the condition given to the change in the voltage determine the ratio of the resistances: R1/R2.
b) What are the values of the resistance of the resistors R1 and R2?
(4 pont)
solution (in Hungarian), statistics
P. 4506. A stationary electron and a positron, which travels at half of the speed of the light, collide. What is the frequency of the two photons which born after the annihilation, if they travel in the direction of the initial velocity of the positron?
(4 pont)
solution (in Hungarian), statistics
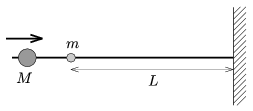
P. 4507. Two small balls are threaded to a horizontal frictionless rod which is attached to the wall. The heavy ball of mass M is moving towards the wall, and the other light ball of mass m (m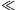 M) is at rest at a distance of L measured from the wall. After the totally elastic collision, the light ball of mass m moves towards the wall and collides with it elastically. Then it moves towards the heavy ball and collides with it and the process is repeated. To what distance can the heavy ball approach the wall? (The two balls can be considered as pointlike objects.)
M) is at rest at a distance of L measured from the wall. After the totally elastic collision, the light ball of mass m moves towards the wall and collides with it elastically. Then it moves towards the heavy ball and collides with it and the process is repeated. To what distance can the heavy ball approach the wall? (The two balls can be considered as pointlike objects.)
(6 pont)
Upload your solutions above.
