KöMaL Problems in Physics, October 2013
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'M'Deadline expired on November 11, 2013. |
M. 335. Measure how the rate of evaporation of vinegar depends on its temperature.
(6 pont)
 |
Problems with sign 'P'Deadline expired on November 11, 2013. |
P. 4561. The accuracy of the measurement of the mass of a steel bearing ball is 1% and that of its diameter is 3%. Using these data what accuracy can be deduced for the density of the steel, from which the ball is made?
(3 pont)
solution (in Hungarian), statistics
P. 4562. We would like to carry 600 bricks to a certain distance. If n bricks are carried together then our speed is . We would like to finish this task in the shortest time. How many bricks should we carry together in one go?
(4 pont)
solution (in Hungarian), statistics
P. 4563. A steam funicular railway is to be built to Hill Gellért. The top of the hill is 84 m higher than its foot. The total length of the straight slope is 140 m. There are two cars of equal masses, hung by cables at the two sides of a pulley, and one of them travels uphill whilst the other one travels downhill. In each car 40 people can travel. The funicular is loaded the most when there are 40 people in the car which is travelling up, while the other car is empty. The mass of each car is 5 tons. The average weight of a passanger is 70 kg. The coefficient of rolling friction on the iron rails is 0.005. Calculate the output of the steam engine in horse power, if one trip lasts for one minute. (The stiffness and the mass of the cable, the rotational inertia of the pulley, and air drag can be neglected in this estimation.)
(4 pont)
solution (in Hungarian), statistics
P. 4564. It is known that the atmospheric pressure at a height of 5.5 km is half, and at a height of 11 km is one-quarterth of the pressure measured at see-level (105 Pa). What is the density of the air at the top of a 3000 metre tall hill, at a temperature of -20 oC?
(4 pont)
solution (in Hungarian), statistics
P. 4565. Any object projected in airless space (e.g. on the Moon) at an initial speed of v0 travels along a parabolic path. How far is the focus of this parabola from the position of the projection? What is the angle of the projection, when the focus of the parabola is at the same height as the initial position of the object?
(5 pont)
solution (in Hungarian), statistics
P. 4566. A model car of mass m=12 kg travels on a horizontal rough surface along a circular path of radius R=5 m. It starts from rest and for a while it has a constant tangential acceleration of a0=2 m/s2, and when its acceleration reaches the value of , then it continues its motion along the circular path at constant speed.
a) Measured from the starting instant, when will the car reach the point at which it started?
b) What is the maximum of the static frictional force?
(5 pont)
solution (in Hungarian), statistics
P. 4567. There is a well-illuminated goldfish at rest in an aquarium, which has thin walls, 12 cm away from the wall. With the help of a lens, which has a power of 10 dioptres, an enlarged image is to be formed on a screen. The image should be five times as big as the fish. Where should the lens and the screen be placed? (The refractive index of water is 1.33.)
(4 pont)
solution (in Hungarian), statistics
P. 4568. There is a resistor of resistance R and a capacitor of capacitance C connected in parallel in a black box. Somebody states that this arrangement at a certain frequency cannot be differentiated from that black box which contains an appropriately chosen resistor and capacitance which are connected in series. Is he or she right?
(4 pont)
solution (in Hungarian), statistics
P. 4569. A hollow insulating sphere of radius R is charged uniformly to a charge of Q. There is a small hole on this sphere. What is the electric field strength at the centre of this hole?
(5 pont)
solution (in Hungarian), statistics
P. 4570. Enrico Fermi thought that the active zone of the nuclear reactor built in 1942 should contain a system of uniformly arranged Uranium and graphite mixture, such that the uranium and the graphite are in powdered form and mixed evenly. Leó Szilárd suggested an inhomogeneous arrangement. According to this spheres were made from the metal Uranium, which were surrounded by graphite blocks. From that time onward all the nuclear reactors has inhomogeneous active zones. Why?
(4 pont)
solution (in Hungarian), statistics
P. 4571. The height of the slope shown in the figure is 30 cm, and its base is 40 cm. A solid cylinder of uniform density, which has the same mass as the slope, rolls down along the slope without slipping. What is the least value of the coefficient of friction between the inclined plane and the horizontal ground if the slope does not slip?
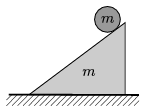
(6 pont)
Upload your solutions above.
