KöMaL Problems in Mathematics, November 2013
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on December 10, 2013. |
K. 391. Add all positive integers for which the remainder on division by 2013 equals the quotient.
(6 pont)
solution (in Hungarian), statistics
K. 392. An underground supporting cable is to be fixed to a pole that will be entirely under ground, even the top of the pole will be buried. When the pit dug for the pole was half done, the workers lowered the pole into the pit. They made the following observation: When the whole pit is dug out, the top of the pole will be exactly twice as much below ground level as it is sticking out of the pit now. Given that the height of the pole is two metres, find the depth of the pit when it is completely dug out.
(6 pont)
solution (in Hungarian), statistics
K. 393. Consider a product whose factors are all 7. Is it possible that the result is a 45-digit number in which the digits 1, 2, 3, 4, 5, 6, 7, 8, 9 occur 9, 8, 7, 6, 5, 4, 3, 2, 1 times, respectively?
(6 pont)
solution (in Hungarian), statistics
K. 394. The sum of the squares of a positive integer and its two neighbours is equal to the sum of five consecutive integers. How many three-digit numbers of this property are there?
(6 pont)
solution (in Hungarian), statistics
K. 395. Where are those points P(x;y) in the rectangular coordinate plane for the coordinates of which xy-2y=3x-6?
(6 pont)
solution (in Hungarian), statistics
K. 396. The points (1;2), (5;A) and (A;7) of the coordinate plane are collinear. Find the value of A.
(6 pont)
 |
Problems with sign 'C'Deadline expired on December 10, 2013. |
C. 1189. Find all integers n such that is also an integer.
(5 pont)
solution (in Hungarian), statistics
C. 1190. Prove that if a trapezium is a cyclic quadrilateral as well as a circumscribed quadrilateral, and furthermore its diagonals are perpendicular then it must be a square.
(5 pont)
solution (in Hungarian), statistics
C. 1191. A truckload of goods consists of n packages weighing 1 kg, n-1 packages weighing 2 kg, n-2 packages of 3 kg, and so on, finally there is 1 package of n kg. Express the average mass of a package as a function of n.
(5 pont)
solution (in Hungarian), statistics
C. 1192. It can be checked by substitution that x=1 is a root of the equation . Solve the equation.
(5 pont)
solution (in Hungarian), statistics
C. 1193. An isosceles triangle of apex angle 120o is drawn on each side of a unit square, on the outside of the square. An equilateral octagon is obtained. In comparison, consider the regular octagon in which the side of the square formed by connecting every other vertex is unity. Find the ratio of the area of the equilateral octagon to the area of the regular octagon.
(5 pont)
solution (in Hungarian), statistics
C. 1194. The sum of three numbers is 6.5, and the difference of the largest and smallest numbers is 4. What is the maximum of the product of the three numbers?
(5 pont)
solution (in Hungarian), statistics
C. 1195. Let a, b and c, respectively, be the lengths of the face diagonals AF, FC and CA of a cuboid ABCDEFGH. Let  ,
,  and
and 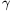 , respectively, denote the angles enclosed by the face diagonals with the diagonal BH of the cuboid. Prove that a.cos
, respectively, denote the angles enclosed by the face diagonals with the diagonal BH of the cuboid. Prove that a.cos  -b.cos
-b.cos  +c.cos
+c.cos 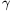 =0 if the length of edge AB is between the lengths of the edges BC and BF.
=0 if the length of edge AB is between the lengths of the edges BC and BF.
(5 pont)
 |
Problems with sign 'B'Deadline expired on December 10, 2013. |
B. 4572. Solve the following simultaneous inequalities on the set of pairs of integers: 11>2a-b, 25>2b-a, 42<3b-a and 46<2a+b.
(3 pont)
solution (in Hungarian), statistics
B. 4573. Prove that among any seven vertices of a regular 27-sided polygon there are four that form a trapezium.
Competition problem from Germany, 2012
(6 pont)
solution (in Hungarian), statistics
B. 4574. Solve the simultaneous equations
ax+by+cz=d,
a2x+b2y+c2z=d2,
where a, b, c, d are distinct real parameters.
Matlap, Kolozsvár, 2013
(4 pont)
solution (in Hungarian), statistics
B. 4575. According to the tradition of the ancient tribe of Head Counters, every year is designated either as lucky or as sinister. For example, 2013 is a lucky year since the first 2013 positive integers can be partitioned into at least two classes such that each class contains the same number of elements and the sum of the elements is also equal in each class. If such a partition does not exist, the year is said to be sinister. Which years are sinister?
Suggested by T. Káspári, Paks
(6 pont)
solution (in Hungarian), statistics
B. 4576. Six distinct points lie on a circle. Three points are selected, and the orthocentre of their triangle is connected to the centroid of the triangle formed by the other three points. Prove that all line segments obtained in this way are concurrent.
Suggested by G. Holló, Budapest
(5 pont)
solution (in Hungarian), statistics
B. 4577. Solve the following equation:
(5 pont)
solution (in Hungarian), statistics
B. 4578. A certain cyclic quadrilateral is also a circumscribed quadrilateral. Given three sides, construct the quadrilateral.
Suggested by A. Faragó András and T. Káspári, Paks
(5 pont)
solution (in Hungarian), statistics
B. 4579. Represent those pairs (a;b) of real numbers in the rectangular coordinate plane for which the polynomial x(x+4)+a(y2-1)+2by of two variables can be expressed as a product of two first-degree polynomials.
(5 pont)
solution (in Hungarian), statistics
B. 4580. The sides of a triangle form a geometric progression, and its angles form an arithmetic progression. Prove that the triangle is equilateral.
(3 pont)
solution (in Hungarian), statistics
B. 4581. Given two perpendicular skew lines and an acute angle  , determine the number of lines that intersect both given lines and encloses an angle of
, determine the number of lines that intersect both given lines and encloses an angle of  with each.
with each.
(5 pont)
 |
Problems with sign 'A'Deadline expired on December 10, 2013. |
A. 599. Two parabolas, and
have the same focus point. The directrix of
meets
at points A and B. The directrix of
meets
at C and D. Show that the points A, B, C and D are concyclic.
Proposed by: Gábor Holló, Budapest
(5 pont)
solution (in Hungarian), statistics
A. 600. Show that for every closed polygonal disk there exists a real number
 such that for arbitrary positive integer n and any points
such that for arbitrary positive integer n and any points there is a point
satisfying
.
Based on a problem of CIIM5, Colombia
(5 pont)
solution (in Hungarian), statistics
A. 601. Let q 1 be an integer. Prove that there is an integer Cq such that for every finite set A of integers |A+q.A|
1 be an integer. Prove that there is an integer Cq such that for every finite set A of integers |A+q.A| (q+1)|A|-Cq holds. (A+q.A is the set of those integers that can be expressed as a+qa' with some a,a'
(q+1)|A|-Cq holds. (A+q.A is the set of those integers that can be expressed as a+qa' with some a,a' A.)
A.)
Schweitzer competition, 2013
(5 pont)
Upload your solutions above.
