KöMaL Problems in Mathematics, February 2014
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on March 10, 2014. |
K. 409. How many different kinds of quadrilateral are there that are divided into two isosceles right-angled triangles by a diagonal?
(6 pont)
solution (in Hungarian), statistics
K. 410. In a regular triangular lattice, a regular triangle is drawn with its sides lying on lattice lines. There are 5995 lattice points in the interior of the triangle. How many lattice points were touched by the pencil drawing the triangle?
(6 pont)
solution (in Hungarian), statistics
K. 411. The power x5 cannot only be calculated by doing the multiplication x.x.x.x.x, but also with fewer multiplications, by calculating partial results (e.g. y=x.x) and obtaining the final answer by multiplying those: y.y.x, which only makes three multiplications altogether. Express the power x23 with less than 10 multiplications to carry out.
(6 pont)
solution (in Hungarian), statistics
K. 412. The centre of a circle of radius lies on the circumference of a unit circle. The two circles divide the plane into four parts, two of which are crescent shaped. What is the area of the smaller crescent?
(6 pont)
solution (in Hungarian), statistics
K. 413. Determine the digits a and b such that the following equality holds: , where
and
denote two-digit numbers.
(6 pont)
solution (in Hungarian), statistics
K. 414. In a chess tournament, every participant plays with every other participant exactly once. Two players withdrew their application, so the actual number of games played were 17 less than planned. How many participants remained?
(6 pont)
 |
Problems with sign 'C'Deadline expired on March 10, 2014. |
C. 1210. We have four sacks of flour. By three measurements, the following information is obtained: the first and second sacks together are lighter than the other two sacks, the first and third together have the same mass as the other two, and the first and fourth together are heavier than the other two. Which sack is the heaviest?
(5 pont)
solution (in Hungarian), statistics
C. 1211. In a convex quadrilateral ABCD, the line drawn through vertex D parallel to line BC intersects side AB at its midpoint F. What is the area of the quadrilateral AFCD if the area of triangle ABD is 4?
(5 pont)
solution (in Hungarian), statistics
C. 1212. Prove that .
(5 pont)
solution (in Hungarian), statistics
C. 1213. Given a rectangle, construct a rectangle of half the area inside it such that the region between the two rectangles forms a frame of uniform width around the small rectangle.
(5 pont)
solution (in Hungarian), statistics
C. 1214. In a class of 30 students, two students are absent. What is the probability that the two of them are next to each other in the alphabetical list of the names? How many students would be in a class where this probability is 0.1?
(5 pont)
solution (in Hungarian), statistics
C. 1215. Prove that if the inscribed circle of a right-angled triangle has unit radius and the length of one leg is rational then the lengths of the other two sides are also rational.
(5 pont)
solution (in Hungarian), statistics
C. 1216. The ideal carnival doughnut weighs 54 grams when done, and 8% is the oil absorbed during frying. It is shaped like a (centrally symmetrical) spherical segment of diameter 78 mm and height 3 cm. The volume of the dough is doubled in frying, and its mass is only increased by the oil absorbed. Before frying, the whole dough weighs 1 kg, and it is kept in a 2.5-litre bowl. Is it possible to cover the bowl with a flat lid?
(5 pont)
 |
Problems with sign 'B'Deadline expired on March 10, 2014. |
B. 4602. The diagonals of a cyclic trapezium are perpendicular. Prove that the distance of the centre of the circumscribed circle from one base is equal to the distance of the intersection of the diagonals from the other base.
(3 pont)
solution (in Hungarian), statistics
B. 4603. The surface area of a right circular cone is A, its volume is V. Prove that A3 72
72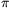 .V2.
.V2.
(4 pont)
solution (in Hungarian), statistics
B. 4604. Solve the equation .
Suggested by B. Kovács, Szatmárnémeti
(5 pont)
solution (in Hungarian), statistics
B. 4605.  and
and  are different real numbers, at least one of which is not an integer. Is it necessarily true that there exists a positive integer n such that
are different real numbers, at least one of which is not an integer. Is it necessarily true that there exists a positive integer n such that  n-
n- n is not an integer?
n is not an integer?
(5 pont)
solution (in Hungarian), statistics
B. 4606. Solve the equation
on the set of positive numbers.
(Matlap, Kolozsvár)
(3 pont)
solution (in Hungarian), statistics
B. 4607. The sides of a triangle are a, b, c. A line passes through the centre of the inscribed circle, and intersects side c at P, and side b at Q. Let AP=p and AQ=q. Prove that .
F. Kacsó, (Matlap, Kolozsvár)
(5 pont)
solution (in Hungarian), statistics
B. 4608. The perpendicular projections of the centroid S of a triangle ABC on sides BC, AC and AB are A1, B1 and C1, respectively. Prove that (with conventional notations) .
(4 pont)
solution (in Hungarian), statistics
B. 4609. Find the smallest positive number c with the following property: For any set of real numbers, it is possible to select some elements of the set such that the distance of their sum from the nearest integer is at most c.
(6 pont)
solution (in Hungarian), statistics
B. 4610. K is the centre of the circumscribed circle of an acute triangle ABC. O is the centre of the inscribed circle, and M is the orthocentre. Is it possible for the points O, K and M to be the vertices of an isosceles triangle?
(Kvant)
(6 pont)
solution (in Hungarian), statistics
B. 4611. Consider the composition of the reflections in the planes of all six faces of a cube in some order. How many different transformations of the spaces are obtained?
(6 pont)
 |
Problems with sign 'A'Deadline expired on March 10, 2014. |
A. 608. Suppose that the convex polygonal disks \(\displaystyle P_1\), \(\displaystyle P_2\) and \(\displaystyle P_3\), lying in the plane, satisfy the property that for arbitrary points \(\displaystyle A\in P_1\), \(\displaystyle B\in P_2\) and \(\displaystyle C\in P_3\), the area of the triangle \(\displaystyle ABC\) is no more than a unit. Prove that there are two different ones among the disks \(\displaystyle P_1\), \(\displaystyle P_2\) and \(\displaystyle P_3\) whose area is at most \(\displaystyle 8\) units in total.
Proposed by: Tamás Fleiner, Budapest
(5 pont)
solution (in Hungarian), statistics
A. 609. Let \(\displaystyle a_1,a_2,\dots,a_n\) and \(\displaystyle b_1,b_2,\dots,b_n\) be complex numbers satisfying \(\displaystyle \mathop{\rm Im} a_j\ge 1\) and \(\displaystyle \mathop{\rm Im} b_j\le -1\) (\(\displaystyle j=1,2,\dots,n\)), and let \(\displaystyle f(z) = \frac{(z-a_1)(z-a_2)\dots (z-a_n)}{(z-b_1)(z-b_2)\dots (z-b_n)}\). Prove that the function \(\displaystyle f'(z)\) has no root in the set \(\displaystyle |\mathop{\rm Im}z|<1\).
(5 pont)
solution (in Hungarian), statistics
A. 610. There is given a prime number \(\displaystyle p\) and two positive integers, \(\displaystyle k\) and \(\displaystyle n\). Determine the smallest nonnegative integer \(\displaystyle d\) for which there exists a polynomial \(\displaystyle f(x_1,\dots,x_n)\) on \(\displaystyle n\) variables, with degree \(\displaystyle d\) and having integer coefficients that satisfies the following property: for arbitrary \(\displaystyle a_1,\dots,a_n\in\{0,1\}\), \(\displaystyle p\) divides \(\displaystyle f(a_1,\dots,a_n)\) if and only if \(\displaystyle p^k\) divides \(\displaystyle a_1+\dots+a_n\).
(5 pont)
Upload your solutions above.
