KöMaL Problems in Physics, November 2014
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'M'Deadline expired on December 10, 2014. |
M. 345. Measure how the height of the water in a vertical conical funnel decreases as a function of time.
(6 pont)
 |
Problems with sign 'P'Deadline expired on December 10, 2014. |
P. 4671. The solar powered Flip Flap, which resembles to a plant with seesawing leaves, is a well known toy. Observing the toy it can be seen that the small plastic flower emerging from a plastic pot is moving left and right, while the two plastic leaves bounces up and down. When the flower is at its furthest position to the right the leaves are at their lowermost point and when the flower is at its left extreme position the leaves are at their uppermost position.

The toy is exposed to light and is weighed with very sensitive (ideal) scales. When will the scales show the greatest weight?
(3 pont)
P. 4672. A solid sphere of volume \(\displaystyle 1~{\rm dm}^3\) made of Aluminium is connected with a thin thread to a wooden sphere made of pine tree, which has a density of \(\displaystyle 0.5~\rm g/cm^3\). The spheres are fully immersed into water and they are at rest.
\(\displaystyle a)\) What is the volume of the wooden sphere?
\(\displaystyle b)\) What is the tension in the thin thread connecting the spheres?
(3 pont)
P. 4673. What is the speed of sound in a sample of Hydrogen gas which is cooled down with liquid air to a temperature of \(\displaystyle -141~{}^\circ\rm C\)?
(4 pont)
P. 4674. A small bead can move frictionlessly on a helix-shaped piece of wire. The symmetry axis of the helix is vertical, its radius is 10 cm, and its pitch is 20 cm. The bead is released at one point of the path. What will its acceleration be after descending 1 complete turn?
(5 pont)
P. 4675. The height of a safe of mass \(\displaystyle M=1000\) kg is \(\displaystyle \ell=1\) m. The safe has a shape of a cube and it has uniform density. The safe is standing on four small legs, in a garage, next to the door of the garage. The coefficient of friction between the legs of the safe and the rough surface of the tiles of the garage is \(\displaystyle \mu_1=0.9\). Outside the garage the ground is a bit smoother, and the coefficient of friction between the ground and the legs is \(\displaystyle \mu_2=0.5\).
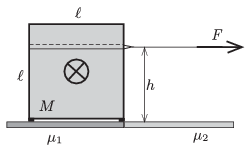
The carrier team uses a horizontal cable at a height of \(\displaystyle h\), and an engine driven winch, to pull out the safe from the garage. The winch (which is to be attached to a strong coloumn) can exert a maximum force of 6000 N. The most-educated (from physics) member of the team states that a stronger winch should be used, because if the weight of the safe is multiplied by the average of the coefficients of friction 7000 N is gained, which exceeds the maximum load of the winch, even if at the beginning with the help of some muscle force two legs of the safe is slid to the smoother ground.
Is the ``Physicist'' of the team right?
(5 pont)
P. 4676. The density of a uniform sphere of radius \(\displaystyle R\) is \(\displaystyle \varrho_1\), except for a smaller spherical region at which the density is \(\displaystyle \varrho_2\) The distance between the centres of the two spheres is \(\displaystyle s\).
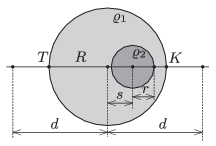
\(\displaystyle a)\) What is the acceleration due to gravity along the line which joins the centres of the spheres at a point which is at a distance of \(\displaystyle d\ge R\) from the centre of the greater sphere?
\(\displaystyle b)\) Let \(\displaystyle s=R/2\) and \(\displaystyle r=R/4\) be. In this case the acceleration due to gravity at point \(\displaystyle K\) is 10% greater then at point \(\displaystyle T\) shown in the figure. What is the ratio of \(\displaystyle \varrho_2/\varrho_1\)?
(4 pont)
P. 4677. The figure shows an easily moveable cart, on the top of which there is a slope of angle of elevation of \(\displaystyle \alpha=30^\circ\), which ends in a circular path. The total mass of the cart with the slope is \(\displaystyle M=0.5\) kg. The path is frictionless everywhere. A small pointlike object of mass \(\displaystyle m=0.3\) kg is placed to the top of the slope, which has a height of \(\displaystyle 2R\), and is released without pushing it to any direction.
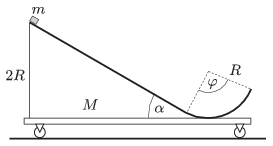
\(\displaystyle a)\) What will the displacement, the velocity and the acceleration of the small object and the cart be, when the small object is at the top of its ascending motion if the central angle of the circular path is \(\displaystyle \varphi=120^\circ\)?
\(\displaystyle b)\) What will the displacement and the velocity of the small object and the cart be at the moment when the small object leaves the circular path if \(\displaystyle \varphi=90^\circ\)?
(5 pont)
P. 4678. A frictionlessly moving piston, which has negligible heat capacity and which is made of some heat conducting material, divides a thermally insulated container into two parts. Initially the chamber at the left contains a sample of diatomic gas and in the chamber at the right there is a sample of monatomic gas, such that the two samples of gas have the same \(\displaystyle V_0\) volume, the same \(\displaystyle p_0\) pressure and also the same \(\displaystyle T_0\) temperature. There is an electric heating element in the left chamber and thermal energy of \(\displaystyle Q\) is added to the gas. Due to the added heat 20% of the molecules of the diatomic gas dissociate to monatomic particles. The energy needed for the dissociation of one mole gas is \(\displaystyle D\).
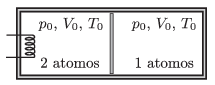
After thermal equilibrium is reached what will the volume of the gas in the left chamber be, and what will its temperature be?
Data: \(\displaystyle p_0=10^5\) Pa, \(\displaystyle V_0=3.3\) liter, \(\displaystyle T_0=300\) K, \(\displaystyle Q=15.6\) kJ és \(\displaystyle D=3\cdot10^5\) J/mol.
(5 pont)
P. 4679. A small object of mass \(\displaystyle m\) and of charge \(\displaystyle q\) slides down frictionlessly along a slope of angle of elevation \(\displaystyle \alpha\) from a height of \(\displaystyle h\). From the midpoint of the slope, it enters into a region of uniform horizontal electric field, and it decelerates and stops at the bottom of the slope. Determine the magnitude of the electric field strength \(\displaystyle E\).
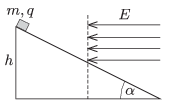
(4 pont)
P. 4680. A bi-concave air lens is made from two watch glasses of radius \(\displaystyle f=10~\)cm and a short piece of tube. Where should it be placed in a 90 cm-long aquarium, filled with water of refractive index \(\displaystyle n=1.33\), such that the image of the figure at the opaque side of the aquarium is formed exactly at the opposite wall of the aquarium?
(4 pont)
P. 4681. The chain of resistors made of \(\displaystyle 3N\) resistors as shown in the figure can be closed in two different ways.
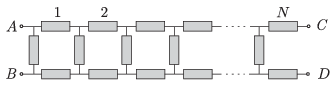
\(\displaystyle a)\) The terminals at points \(\displaystyle A\) and \(\displaystyle C\) are connected and also the terminals at point \(\displaystyle B\) and \(\displaystyle D\) are connected.
\(\displaystyle b)\) The terminals at points \(\displaystyle A\) and \(\displaystyle D\) are connected and also the terminals at \(\displaystyle B\) and \(\displaystyle C\) are connected. (Möbius band.)
In which case will the equivalent resistance of the system between \(\displaystyle A\) and \(\displaystyle B\) be greater?
(6 pont)
Upload your solutions above.
