KöMaL Problems in Physics, December 2014
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'M'Deadline expired on January 12, 2015. |
M. 346. Roll a solid cylinder along different horizontal surfaces, such that it rolls without skidding. According to the measured data determine the coefficient of kinetic friction of that object which would have the same acceleration as the centre of mass of the cylinder, and which would slide without rotation along the horizontal.
(6 pont)
 |
Problems with sign 'P'Deadline expired on January 12, 2015. |
P. 4682. Suppose that the magnitude of the acceleration of a lift when it starts moving upward is the same as that of its deceleration when it stops at some level. What is the value of this acceleration, if at the departure the weight of a passenger is \(\displaystyle k\) times as much as his or her weight at the arrival?
(3 pont)
P. 4683. There are a lot of alike \(\displaystyle 100~\Omega\) resistance resistors in the lab. Two of them are connected in series to a 120 V voltage supply. How many resistors are to be connected in parallel to one of the resistors, in order that the power dissipated at the other reaches the value of 100 W?
(3 pont)
P. 4684. Starting at the centre of the curvature of a spherical concave mirror a point-like object moves uniformly along a straight line until it reaches the pole of the mirror. Determine the relationship between the position of its image and the elapsed time and plot the graph of this function.
(4 pont)
P. 4685. The object of mass \(\displaystyle M=4m\), shown in the figure can freely slide along the horizontal. The curved part of its surface is horizontal at its right side. A small body of mass \(\displaystyle m\) is placed to the object of mass \(\displaystyle M\) at a height of \(\displaystyle H\), measured from the horizontal tabletop, and then the system is released. When the small object of mass \(\displaystyle m\) hits the table the two objects are at a distance of \(\displaystyle d=0.6\) m. Friction is negligible everywhere and \(\displaystyle h=0.2\) m.
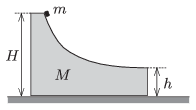
\(\displaystyle a)\) What are the speeds of the two objects at the moment when the small one of mass \(\displaystyle m\) leaves the big one of mass \(\displaystyle M\)?
\(\displaystyle b)\) At what speed does the small object hit the table?
\(\displaystyle c)\) Calculate the height \(\displaystyle H\).
(4 pont)
P. 4686. Two alike discs of mass \(\displaystyle m\) and of radius \(\displaystyle R\) touch each other and move with the same velocity perpendicularly to the line segment which joins their centres of mass, along the surface of a horizontal air-cushioned tabletop. There is a third disc of mass \(\displaystyle M\) and of radius \(\displaystyle R\) at rest, at a point on the perpendicular bisector of the line segment joining the centres of mass of the two moving discs. The two moving discs collides totally elastically with the third one, which is at rest. There is no friction between the rims of the discs.
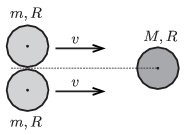
\(\displaystyle a)\) If \(\displaystyle M=m\), what will the speed of the discs be after the collision and what is the direction of their motion?
\(\displaystyle b)\) What should the ratio of \(\displaystyle M/m\) be in order that after the collision the two discs of mass \(\displaystyle m\) move perpendicularly to their initial velocity?
(5 pont)
P. 4687. There are two point-like masses at some distance from each other in the outer space. If one of them is fixed, then the other will hit it after a time of \(\displaystyle T_1=6\) minutes. In the reversed case, this time is \(\displaystyle T_2=8\) minutes. How much time elapses until the collision if both objects can move freely?
(5 pont)
P. 4688. A thermally insulated container is divided into two parts by a wall of negligible volume. The volume of the two parts are 2 dm\(\displaystyle {}^3\) and 3 dm\(\displaystyle {}^3\). In the 2 dm\(\displaystyle {}^3\) part there is a sample of Helium gas at a temperature of 300 K and at a pressure of \(\displaystyle 2\cdot10^5\) Pa, and in the other part there is a sample of Oxygen gas at a temperature of 200 K and at a pressure of \(\displaystyle 10^5\) Pa. What will the temperature and the pressure of the mixture of gases if the wall is eliminated?
(4 pont)
P. 4689. The working substance in a thermodynamic heat engine is a sample of diatomic ideal gas, which is taken through a cyclic process which consists of two isobaric and two isochoric processes. The highest temperature of the gas in this cyclic process is 500 K. At those two states when the gas changes from the isochoric process to the isobaric process the temperatures are equal.
What is the lowest temperature of the gas during the cyclic process if the greatest possible efficiency of the heat engine working between the two extreme temperature values could be 9.9-times as much as the thermodynamic efficiency of the engine in the above described case?
(5 pont)
P. 4690. Two well-insulated condensers are charged on order to experiment with them. If they are connected in series, such that the oppositely charged terminals are connected, then altogether 166 V is measured across them. If they are connected in parallel, such that the same terminals are connected then the voltage across them is 74.4 V. In this latter case the energy loss is equal to the original energy of that condenser of capacitance \(\displaystyle 10~\mu \rm F\), which had smaller voltage across its plates.
\(\displaystyle a)\) What was the original voltage of the two condensers?
\(\displaystyle b)\) What is the capacitance of the other condenser?
(5 pont)
P. 4691. The total cost of building the Solar Park at Újszilvás was 618 million Forints. The peak power output of the park is 400 kW, and it generated 685 MWh electrical energy in the first complete year, after establishing it. The peak power output of the nuclear power station at Paks is 2000 MW and in 2013 it generated 15.37 TWh electrical energy.
\(\displaystyle a)\) How can it be reasoned that the ratio of the peak powers is not the same as the ratio of the annual energy generation?
\(\displaystyle b)\) What would the total cost of replacing the nuclear power station at Paks to solar parks be?
(4 pont)
P. 4692. A straight coil of length \(\displaystyle L=20\) cm, of cross-section of \(\displaystyle A=12~\rm cm^2\) and of number of turns \(\displaystyle N=400\) can rotate in the horizontal plane along a vertical axle through its centre. The coil is in uniform horizontal magnetic field of induction \(\displaystyle B=0.05\) T. Initially the coil is perpendicular to the magnetic induction, and there are two unstretched springs attached to both of its ends, as shown in the figure. The other ends of the springs are also fixed and initially the springs are perpendicular to the coil. The spring constant of the springs is \(\displaystyle D=24\) N/m, and their length is \(\displaystyle \ell_0=20\) cm.
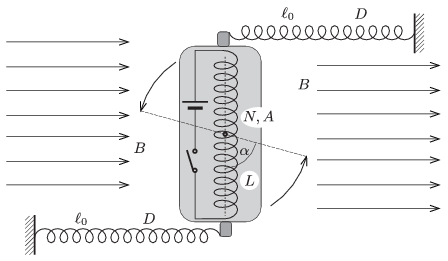
After the switch is turned on, there will be current in the coil. What is the current in the coil if the coil will be in equilibrium after turning an angle of \(\displaystyle \alpha=60^\circ\)?
(6 pont)
Upload your solutions above.
