KöMaL Problems in Informatics, January 2015
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'I'Deadline expired on February 10, 2015. |
I. 364. We are controlling a robot on an \(\displaystyle n\times n\) grid. The robot can move in four directions along empty grid cells. The robot cannot pass through the four walls surrounding the board, and there are also some obstacles inside blocking its way. To control the robot, we use the letters F, L, J and B (= up, down, right, left): when pressing any of these keys, the robot starts moving in a straight line in the given direction until it touches an obstacle or a wall. The example shows a grid with \(\displaystyle n=10\) and with some obstacles (``X'').
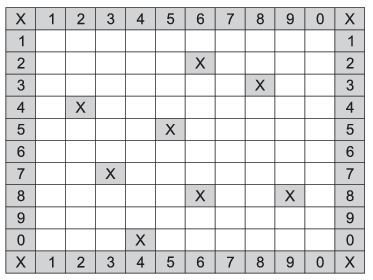
Your program i364 should solve the following tasks.
1. Read the board description from the text file palya.txt. The first line of the file contains the value of \(\displaystyle 1\le n\le 20\), the next line describes the number of obstacles, then each successive line contains the (column and row) coordinates (separated by a space) of the obstacles.
2. You should draw a map of the board by using X characters to denote the corners and inner obstacles, and the last digits of the column and row coordinates to denote the walls on each side.
3. Prompt the user to enter a column/row pair, then check if the corresponding grid cell is empty. The output should be a message such as ``The cell (3,5) is empty.''
4. Choose a free cell randomly and store its location for later use. A message such as ``The starting cell of the robot is (6,4).'' should be displayed.
5. Determine the coordinates of the cells that can be reached in one step (that is, in a straight line) by using the given starting cell. By using the previous example, the output would be ``The cells (6,3), (6,7), (3,4) and (10,4) can be reached in one step.''
6. Prompt the user to enter a character string encoding commands to the robot. Apart from the lowercase and uppercase characters denoting valid directions, all other characters should be ignored. The following data should be written in the text file mozgas.txt: the starting cell coordinates, and the coordinates of the cells the robot stops at when executing the movement commands. The robot should start from the cell chosen in Task 4 above. A sample user input can be ``FFjLeBF'' for example.

7. The previous user input should be corrected and simplified as follows: the modified version should contain only uppercase letters encoding valid directions, but directions that do not change the robot position on the given board should also be ignored. The modified string for the previous example thus becomes ``The modified string of directions is FJLBF''.
The table in the example contains a sample input (``Példa bemenet'') and output (``Példa kimenet'').
The source code (i364.pas, i364.cpp, ...) without the .exe or any other auxiliary files generated by the compiler but with a short documentation (i364.txt, i364.pdf, ...), also describing which developer environment to use for compiling the source, should be submitted in a compressed file i364.zip.
(10 pont)
I. 365. There are five gates to the depot of a trading company. The company owns 10 trucks. Due to the length of the loading and unloading process, a truck can pass through a gate at most once in every hour. A truck can use any of the gates to enter or exit the depot, but they have to stop briefly there to electronically register their number plates (``Rendszám'' in the example below), the time (1-100 in the ``Óra'' column) they pass through the gate, their direction (in or out, that is, ``Be'' or ``Ki'' in the ``Irány'' column), the gate number (1-5, ``Kapu'') and the truck weight (0,0-100,0 in tons in the ``Súly'' column - notice that here a comma is used instead of a decimal dot).

The file i365.zip (downloadable from our web page) contains the data recorded at the five gates (kapu1.txt, kapu2.txt, ..., kapu5.txt) and the data corresponding to the trucks (teherautok.txt, a tabulator-separated and UTF-8 encoded text file).
In your solution you
- may want to use formulae, functions or links whenever possible;
- can perform auxiliary computations only to the right of column E;
- should not use macros or user-defined functions.
1. In your spreadsheet application open the files containing the data recorded at the gates, then copy their content into a single table in a new sheet Raktár. Make sure that this new table has only one header (unnecessary headers should be deleted). You should save the table in the default application file format with name i365.
2. Place the truck data in a sheet Teherautók so that the first data piece is put into cell A1.
3. The data on the Raktár sheet should now be sorted according to the truck number plates, then, for the same truck, according to when they passed the gate.
Answers to the following questions should be displayed in the Teherautók sheet; a short text describing the actual cell content should precede the cells or should be put in the column headers.
4. For each truck you should determine how many tons of goods they transported in the depot and out of the depot, respectively, in the given period. The amount of transported goods is the difference between the full truck weight and empty truck weight measured at the gate.
5. Give the number plate of the truck that delivered the largest amount of goods into the depot.
6. Display for each truck whether they were in the depot or outside the depot before passing through Gate 1.
7. Read a time value in the given period and display the number of trucks in the depot at that time. Trucks entering or exiting the depot in that hour should not be taken into account.
8. Display, based on the given data, at least how many trucks broke the rules and did not stop at the gates to register their data.
9. Determine the peak hour with respect to truck traffic.
Your sheet (i365.xlsx, i365.ods,...) containing a short documentation (i365.txt, i365.pdf, ...) and also describing the name and version number of the spreadsheet application, should be submitted in a compressed file (i365.zip).
Downloadable file: i365.zip
(10 pont)
I. 366. The logo of our journal appears on our web page, on Facebook and in the printed volumes as well. We would like to recreate the web page logo by using animation. Your solution should use the same shapes as in the static version; the final result can be slightly different.

The animation should include some translation, rotation, scaling and changing colors. The overall effect should be elegant and decent. In connection with the SVG, you may visit the following pages:
\(\displaystyle \bullet\) http://svg.elte.hu/.
\(\displaystyle \bullet\) http://tutorials.jenkov.com/svg/index.html.
Your solution in HTML format (i366.html) and containing the animation in an ``svg'' tag should be submitted. The HTML document should contain any links that proved to be useful in your work.
(10 pont)
 |
Problems with sign 'S'Deadline expired on February 10, 2015. |
S. 95. George has five identical decks of playing cards. Each card contains an integer, and no integer is found on two different cards in a deck. So if a particular number turns up in a deck, then that number can also be found in each of the other decks exactly once. George likes to keep his cards in a particular order: he ordered all five decks in the same way.
During the night, however, a wicked kobold visited George's house. The kobold chose a deck and drew some cards out of it, then put those cards back into the deck in some way (not necessarily to their original place, but into the same deck). The kobold then performed this operation on each of the remaining four decks. But if a particular integer was relocated in a deck, the corresponding card with that integer was not touched again in the other decks. After waking up in the morning, George was perplexed. Fortunately, you can help him restore the original card order in all decks.
Your program should read the value of \(\displaystyle N\) (\(\displaystyle 1\le N\le 50\;000\)) from the first line of the standard input, then the (space-separated) \(\displaystyle a_i\) integers from the following \(\displaystyle 5\cdot N\) lines. The first \(\displaystyle N\) numbers describe the card order in the first deck after the kobold's operation, the second \(\displaystyle N\) numbers describe the new card order in the second deck, and so on. The first \(\displaystyle N\) lines of the standard output should contain the original, common deck order.
In the example, ``Példa bemenet'' is a sample input, and ``Példa kimenet'' is the corresponding output. To save some space in the example, the \(\displaystyle 5\cdot N\) input lines and the \(\displaystyle N\) output lines are now printed in one line, with the / symbol denoting end-of-line characters.
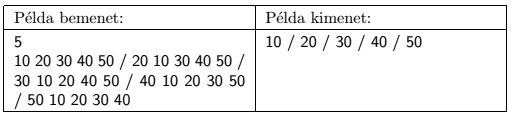
Scoring and bounds. You can obtain 1 point for a brief and proper documentation clearly describing your solution. Nine further points can be obtained provided that your program solves any arbitrary valid input within 1 second of running time.
The source code (s95.pas, s95.cpp, ...) without the .exe or any other auxiliary files generated by the compiler but with a short documentation (s95.txt, s95.pdf, ...), also describing which developer environment to use for compiling the source, should be submitted in a compressed file s95.zip.
(10 pont)
$Var(Body)
Upload your solutions above
