KöMaL Problems in Physics, February 2015
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'M'Deadline expired on March 10, 2015. |
M. 348. Not only the length of a loaded helical spring changes, but - if one of the ends of the spring is free to move - to some extent the whole spring is ``twisted''. Measure how the angular displacement of the end of the spring depends on the load. Carry out the measurement for springs which have different number of turns and for springs which have different strength.
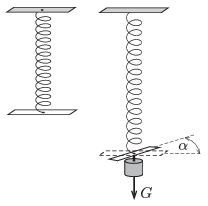
(6 pont)
 |
Problems with sign 'P'Deadline expired on March 10, 2015. |
P. 4704. Calculate the cubic content of the spherical bulb of a mercury in glass thermometer at a temperature of \(\displaystyle 0~{}^\circ\)C, if the cubic content of that part of the thermometer which is between the \(\displaystyle 0~{}^\circ\)C mark and the \(\displaystyle 100~{}^\circ\)C mark is 5 mm\(\displaystyle {}^3\). The coefficient of linear expansion of glass is \(\displaystyle 8\cdot 10^{-6}~(1/{}^\circ \rm C)\), and the coefficient of volume expansion of mercury is \(\displaystyle 1.8 \cdot 10^{-4}~(1/{}^\circ \rm C)\).
(3 pont)
P. 4705. The International Space Station completes a whole revolution around the Earth in 92 minutes. Suppose that its path is circular. How high above the surface of the Earth does it revolve? How much does its period change (between two corrections of its path) if its height changes approximately 100 meters during one day?
(4 pont)
P. 4706. An object slides down frictionlessly from the top of a fixed straight slope of base 30 cm. At least how long does it take for the object to slide down?
(4 pont)
P. 4707. An object of mass \(\displaystyle m=0.2\) kg and another one of mass \(\displaystyle 4m\) can move frictionlessly along a horizontal surface. The greater mass object is attached to an unstretched spring of spring constant \(\displaystyle D=320\) N/m. (The spring is designed for both compression and tension.) The smaller object collides head-on at a speed of \(\displaystyle v_0=5\) m/s with the stationary heavy object. The collision is totally elastic.
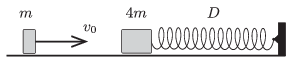
\(\displaystyle a)\) What is the maximum compression of the spring?
\(\displaystyle b)\) What will the maximum speed of the object attached to the spring be, and what is the greatest extension of the spring?
(4 pont)
P. 4708. A rectangle and a square shaped sheets are rotated about an axle through their centres, the axle is perpendicular to the plane of the sheets. The two sheets have the same mass, same width and the same density. One side of the rectangle is half of its other side. Which sheet has the greater rotational inertia? (It is not necessary to calculate the rotational inertias of the two objects separately.)
(4 pont)
P. 4709. The mass of a uniform density plastic cube of edge 2 dm is 1.0 kg. The Young's modulus of its material is \(\displaystyle 10^7~\rm{N/m}^2\).
\(\displaystyle a)\) How much is this cube compressed if it is placed to a horizontal surface?
\(\displaystyle b)\) How much does the height of its centre of mass decrease?
(5 pont)
P. 4710. Some ice at a temperature of \(\displaystyle 0~{}^\circ\)C is added to 1 kg water at a temperature of \(\displaystyle 2~{}^\circ\)C. The mixture is in a thermally insulated container and the amount of ice is such, that it just melts whilst the final temperature of the water will be \(\displaystyle 0~{}^\circ\)C.
\(\displaystyle a)\) Will the entropy of the system increase or decrease?
\(\displaystyle b)\) Give numerical estimation for the change in the entropy of the system.
(5 pont)
P. 4711. Six alike simple pendulums are made of electrically insulating threads of negligible mass and of small metal spheres of mass 5 g. The length of each pendulum is 0.5 m. The six pendulums are hung at the same point, and then they are all rotated about a vertical axis through this point. After a long enough time each small sphere revolves along a circular path of radius \(\displaystyle r\) in a horizontal plane.
\(\displaystyle a)\) What is the radius \(\displaystyle r\) of the path, if the period of the motion is 1 s?
\(\displaystyle b)\) What same amount of charge should be added to the spheres in order that they stay at the circumference of the same radius of circle \(\displaystyle r\), without rotation?
(4 pont)
P. 4712. To which two points of a uniform density and uniform cross section copper ring should an electrical voltage supply be connected in order that the magnetic flux density induced by the current in the ring is to be zero at the centre of the ring?
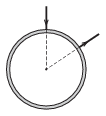
(4 pont)
P. 4713. A small ball of mass \(\displaystyle m\) and of charge \(\displaystyle Q\) is hanging on a piece of thread in uniform vertical magnetic field of magnetic induction \(\displaystyle B\). The ball is given an initial velocity such that it undergoes uniform circular motion in a horizontal plane. At another occasion the ball is started such that it moves in the magnetic field along the same radius of circle in the horizontal, but in the opposite direction as it did in the previous case.
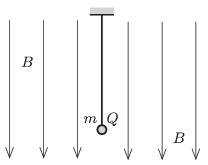
\(\displaystyle a)\) Determine the ratio of the two tensions in the thread in the two cases.
\(\displaystyle b)\) What is the difference between the magnitudes of the angular speeds of the two motions?
(4 pont)
P. 4714. A satellite orbits about the Earth along an elliptical path. The major axis of the ellipse is \(\displaystyle 2a\) and its minor axis is \(\displaystyle 2b\). Determine the velocity of the satellite
\(\displaystyle a)\) at that point of its path which is the closest to the Earth;
\(\displaystyle b)\) at that point of its path which is the furthest from the Earth;
\(\displaystyle c)\) at a point which is at a distance of \(\displaystyle r\) from the centre of the Earth.
(5 pont)
Upload your solutions above.
