KöMaL Problems in Mathematics, April 2015
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'C'Deadline expired on May 11, 2015. |
C. 1287. The positive integers are written on a large squared sheet of paper, arranged in a spiral, as shown in the figure. What numbers are written in the fields above and below 2015?
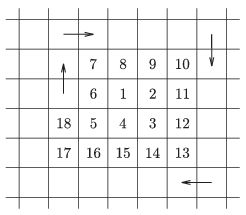
(5 pont)
C. 1288. \(\displaystyle H\) is the point lying closer to vertex \(\displaystyle B\) that divides side \(\displaystyle AB\) of parallelogram \(\displaystyle ABCD\) in a 1 to 2 ratio. \(\displaystyle F\) is the midpoint of side \(\displaystyle BC\). In what ratio does the intersection of line segments \(\displaystyle AF\) and \(\displaystyle DH\) divide them?
(5 pont)
C. 1289. We have 5 five-forint coins, 10 ten-forint coins and 20 twenty-forint coins (HUF, Hungarian currency). In how many different ways can we pay 500 forints with these coins?
(5 pont)
C. 1290. Solve the equation \(\displaystyle 2xy+2x-5y=40\) on the set of pairs of integers \(\displaystyle (x;y)\).
(5 pont)
C. 1291. Find the point on the \(\displaystyle x\)-axis where the line segment formed by points \(\displaystyle A(2;4)\) and \(\displaystyle B(6;1)\) subtends the greatest angle.
(5 pont)
C. 1292. Solve the equation \(\displaystyle \big(3\sqrt{3}\,\big)^n- \big(2\sqrt{2}\,\big)^n =2^n+3^n+\sqrt{6}^{\,n}\) on the set of positive integers.
(5 pont)
C. 1293. Alpha & Co. manufacture tennis balls and sell them in packets of four, arranged in a pyramid in a regular tetrahedral box (figure 1). Another manufacturer, APHLA, also sells tennis balls in four-packets, arranged in a column in a tall cylindrical box closed at both ends (figure 2). What is the difference between the surface areas of the two boxes if the diameter of a tennis ball is 6.50 cm?
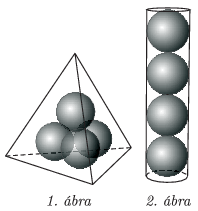
(5 pont)
 |
Problems with sign 'B'Deadline expired on May 11, 2015. |
B. 4705. Let \(\displaystyle p\) denote an odd prime number. Show that the equation \(\displaystyle x^2 + px = y^2\) has exactly one solution on the set of pairs of positive integers.
Suggested by: B. Németh, Budapest
(4 pont)
B. 4706. The sides of rectangle \(\displaystyle ABCD\) are \(\displaystyle AB= \frac{\sqrt{5}+1}2\) and \(\displaystyle BC=1\). Let \(\displaystyle E\) be the point in the interior of line segment \(\displaystyle AB\) with \(\displaystyle AE=1\). Show that \(\displaystyle \angle ACE= 2\cdot \angle EDB\).
Suggested by Sz. Miklós, Herceghalom
(3 pont)
B. 4707. Let \(\displaystyle t>1\) be an odd integer. Prove that there exist only a finite number of pairs of integers \(\displaystyle n\) and \(\displaystyle k\), not smaller than \(\displaystyle t\) such that \(\displaystyle S=\binom{n}{t} + \binom{k}{t}\) is a prime.
Suggested by B. Maga, Budapest
(5 pont)
B. 4708. \(\displaystyle O\) is the centre of the circumscribed circle of triangle \(\displaystyle ABC\), and \(\displaystyle M\) is the orthocentre. Point \(\displaystyle A\) is reflected in the perpendicular bisector of side \(\displaystyle BC\), \(\displaystyle B\) is reflected in the perpendicular bisector of side \(\displaystyle CA\), and finally \(\displaystyle C\) is reflected in the perpendicular bisector of side \(\displaystyle AB\). The reflections are denoted by \(\displaystyle A_1\), \(\displaystyle B_1\), \(\displaystyle C_1\), respectively. Let \(\displaystyle K\) be the centre of the inscribed circle of triangle \(\displaystyle A_1B_1C_1\). Prove that point \(\displaystyle O\) bisects line segment \(\displaystyle MK\).
Suggested by B. Bíró, Eger
(5 pont)
B. 4709. Solve the simultaneous equations
\(\displaystyle x^{2}+y^{2}=13,\)
\(\displaystyle x^{3}+y^{3}=35.\)
Suggested by J. Szoldatics, Budapest
(3 pont)
B. 4710. \(\displaystyle \mathcal P\) is a set of points in the plane such that every disc of unit radius has at least one point of \(\displaystyle \mathcal P\) in its interior. Is it true that there exists a closed disc of unit radius that contains at least three points of \(\displaystyle \mathcal P\)?
(4 pont)
B. 4711. Let \(\displaystyle f(x)=\frac{4^x}{4^x+2}\). Calculate the value of the sum \(\displaystyle f(0/2015)+ f(1/2015)+f(2/2015)+\dots +f(2014/2015)+f(2015/2015)\).
(5 pont)
B. 4712. What percentage of a pencil gets wasted? Assume that a pencil is a cylinder, infinitely long, and the graphite rod inside is also cylindrical. The axes of the two cylinders coincide. When the pencil is sharpened, its point is a perfect cone with an apex angle of 12 degrees. When we write with the pencil, its axis always encloses a 42-degree angle with the plane of the paper. We keep using the pencil until we can no longer write with it since no matter how we rotate it about its axis, the wood will scratch the paper. Then the pencil is sharpened again to the shape of a 12-degree cone, but never longer, that is, the tip of the pencil never changes during sharpening, it only wears in writing. What percentage of the graphite is wasted by scraping it off with the sharpener? Will someone holding the pencil at a 45-degree angle waste more than that or less? If so, by how much?
Suggested by E. M. Gáspár, Budapest
(5 pont)
B. 4713. A circle passing through vertices \(\displaystyle B\) and \(\displaystyle C\) of triangle \(\displaystyle ABC\) intersects side \(\displaystyle AB\) at \(\displaystyle D\), and side \(\displaystyle AC\) at \(\displaystyle E\). The intersection of lines \(\displaystyle CD\) and \(\displaystyle BE\) is \(\displaystyle O\). Let \(\displaystyle M\) denote the centre of the inscribed circle of triangle \(\displaystyle ADE\), and let \(\displaystyle N\) denote the centre of the inscribed circle of triangle \(\displaystyle ODE\). Prove that line \(\displaystyle MN\) bisects the smaller arc \(\displaystyle DE\).
(6 pont)
 |
Problems with sign 'A'Deadline expired on May 11, 2015. |
A. 641. Determine whether there is a finite, nonempty subset \(\displaystyle S\) of the square grid in the plane such that every element of \(\displaystyle S\) has at least two neighbours in \(\displaystyle S\) and \(\displaystyle S\) does not contain four points that are the vertices of a square (with sides not necessary parallel to the coordinate axes)?
Proposed by: Mátyás Sustik, San Francisco
(5 pont)
A. 642. Let \(\displaystyle n\ge3\), let \(\displaystyle x_1,\ldots,x_n\) be nonnegative numbers, and let \(\displaystyle A=\sum_{i=1}^n x_i\), \(\displaystyle B= \sum_{i=1}^n x_i^2\) and \(\displaystyle C= \sum_{i=1}^n x_i^3\). Prove that \(\displaystyle (n+1)A^2B + (n-2)B^2 \ge A^4 + (2n-2)AC\).
(5 pont)
A. 643. For every positive integer \(\displaystyle n\), let \(\displaystyle P(n)\) be the greatest prime divisor of \(\displaystyle n^2+1\). Show that there are infinitely many quadruples \(\displaystyle (a,b,c,d)\) of positive integers that satisfy \(\displaystyle a<b<c<d\) and \(\displaystyle P(a)=P(b)=P(c)=P(d)\).
(5 pont)
Upload your solutions above.
