KöMaL Problems in Physics, September 2015
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'M'Deadline expired on October 12, 2015. |
M. 352. Measure the spring constant of the toy called jumping frog. One cane make the frog jump such that the sucker is pressed against the bottom disc, in the direction of the axis of the spring. (If the jumping frog is not available, one can make experiments with a retractable ballpoint pen.)

(6 pont)
 |
Problems with sign 'P'Deadline expired on October 12, 2015. |
P. 4748. Can it be possible that the ice-cream ball, which was dropped from the tower called Károly-kilátó in the city of Sopron, melts before it reaches the ground?
(3 pont)
P. 4749. A parachutist descends uniformly at a speed of 8 m/s in calm weather. What will the speed of the parachutist be if there is a 6 m/s crosswind?
(3 pont)
P. 4750. Silver-gold alloys can be made in any ratio of the two constituents. The weight of a particular piece of this type of alloy in air is 15 N, whilst its weight in water is 14 N. What is the percent composition by mass of gold in the alloy?
(4 pont)
P. 4751. What can be observed if the handle of a resonating tuning fork
\(\displaystyle a)\) touches the tabletop, or
\(\displaystyle b)\) is emerged into water?
Explain the observations.
(4 pont)
P. 4752. The string of a bow is pulled by a force of 200 N, such that the arrow is moved backwards by a distance of 50 cm. The applied force is proportional to the displacement of the midpoint of the string. With this bow an arrow of mass 40 g is shot vertically upwards. To what maximum height can the arrow fly if 40% of the elastic energy is used?
(4 pont)
P. 4753. The beat frequency of two organ pipes of lengths 80 cm and 81 cm is 2.6 Hz, when both resonate at its fundamental frequency. Calculate the fundamental frequencies of the pipes and the speed of sound in air.
(4 pont)
P. 4754. 4 litres of water at a temperature of \(\displaystyle 30\,^\circ\)C is poured into a copper hemisphere shaped container of volume \(\displaystyle 4~{\rm dm}^3\). The temperature of water decreases by \(\displaystyle 3\,^\circ\)C, whilst the temperature of the container increases by \(\displaystyle 27\,^\circ\)C. What is the width of the wall of the container?
(4 pont)
P. 4755. We have four filament lamps rated at 4.5 V, and two rechargeable batteries, one rated at 12 V and the other at 3 V. Make a circuit from the given elements, such that all the filament lamps are operated at their working temperatures.
(4 pont)
P. 4756. A circular ring is made of a piece of metal wire of resistivity \(\displaystyle \varrho\) and of width \(\displaystyle 2a\). The radius of the central circle of the ring is \(\displaystyle r\) (\(\displaystyle r\gg a\)). This ring is placed into uniform magnetic field of magnitude \(\displaystyle \boldsymbol{B}_0\), which is perpendicular to the plane of the ring. Then the magnetic induction is decreased uniformly to zero in a time of \(\displaystyle \Delta t\). Determine the magnitude of the induced magnetic field, \(\displaystyle B_{\rm ind}\), at the centre of the ring.
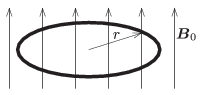
(5 pont)
P. 4757. The work function of the cathode of a photocell in a circuit is \(\displaystyle 6\cdot 10^{-19}\) J. Ultraviolet wave of wavelength 250 nm hits the cathode perpendicularly.
\(\displaystyle a)\) What is the stopping potential at which the photo-current becomes zero?
\(\displaystyle b)\) What is the linear momentum given to the cathode, during one elementary process, if the emitted electron is ejected oppositely to the direction of the radiation?
\(\displaystyle c)\) Let us change the frequency of the radiation. At most by what factor can the linear momentum of the emitted electron be greater than that of the entering photon?
(5 pont)
Upload your solutions above.
