KöMaL Problems in Mathematics, September 2015
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on October 12, 2015. |
K. 463. A certain amount of money was divided among four people. The first one got 3000 forints (HUF, Hungarian currency) more than one third of the total, the second one got 6000 forints more than one fourth of the total, the third one got 9000 forints more than one fifth of the total, and the fourth one got 12 000 forints more than one sixth of the total. What was the total?
(6 pont)
K. 464. A teacher instructed the students to count from 1 to 1000 while keeping the following rules. In each calculation step, one can choose to either multiply the previous result by a fixed one digit number \(\displaystyle a\) selected in advance, or just add 1 to it. Which number should be chosen to be \(\displaystyle a\) in order to be able to reach 1000 in the least number of steps?
(6 pont)
K. 465. A treasure trunk has an electronic lock mechanism controlled by eight switches. Every switch has two settings: on or off. The lock opens if each switch is on. It is possible to change the setting of any switch to the opposite. However, the electronic sensors will detect which switch has been manipulated, and as a result, three other switches will be automatically changed, too. (These automatic changes will not generate further switches changing.) The table below shows which switch induces which further switches to change. (For simplicity, the switches are numbered.)
|
\(\displaystyle a)\) Initially, every switch is off, except for 6 and 7. The trunk can now be opened by manually changing the setting of two appropriate switches. Which two?
\(\displaystyle b)\) Initially, every switch is off, except for 7. Is it possible to open the trunk now by manipulating the appropriate switches?
(6 pont)
K. 466. How many integers are there from 1 to 2015 such that their decimal representation contains a digit of 5, but does not contain any digit of 7?
(6 pont)
K. 467. Let \(\displaystyle p\) denote a prime number greater than 3 and less than 1000. What are the chances that \(\displaystyle p−1\) or \(\displaystyle p+1\) is divisible by 6?
(6 pont)
K. 468. \(\displaystyle x\) denotes a positive integer such that the fraction \(\displaystyle \frac{30−x}{91}\) can be rationalized. Find all possible values of the fraction, expressed in lowest terms.
(6 pont)
 |
Problems with sign 'C'Deadline expired on October 12, 2015. |
C. 1301. Prove that if \(\displaystyle x_1\) and \(\displaystyle x_2\) are positive real numbers, then
\(\displaystyle (x_1+x_2+1) \left(\frac{1}{x_1}+\frac{1}{x_2}+1\right)\ge 9. \)
(5 pont)
C. 1302. The tangents drawn from an exterior point \(\displaystyle P\) to a given circle of radius \(\displaystyle r\) and centre \(\displaystyle O\) touch the circle at \(\displaystyle Q\) and \(\displaystyle R\). What should be the distance \(\displaystyle |OP|\) so that the area of quadrilateral \(\displaystyle PQOR\) is equal to the area of the circle?
(5 pont)
C. 1303. The area of a rectangular origami sheet is \(\displaystyle 130~\rm{cm}^2\). The sheet is folded symmetrically by forming a regular triangle with two adjacent vertices turned inwards, as shown in the figure. Find the lengths of the sides of the original sheet.

(5 pont)
C. 1304. Two players are playing the following game: They take turns in writing a natural number 1 to 10 on a blackboard. It is only allowed to write a number that does not divide any of the numbers written on the board previously. If a player is not able to write a new number on the board, he loses the game. Show that the starting player has a winning strategy.
(5 pont)
C. 1305. A spiral is made out of a square of side \(\displaystyle n\) units, as shown in the figure, by always breaking the line 1 unit before reaching the already existing part of the spiral. Similarly, a spiral is made out of a regular triangle of side \(\displaystyle 1.8n\) units by breaking the line 1.8 units before closing up. (The diagram shows the two spirals for the case of \(\displaystyle n = 4\).) For what value of n will the lengths of the two spirals be equal?
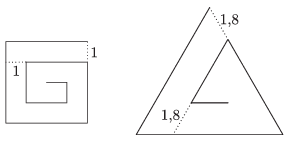
(5 pont)
C. 1306. Prove that if a triangle has two sides that are at most as long as the corresponding altitudes each, then the triangle is an isosceles right-angled triangle.
(5 pont)
C. 1307. For what real number q will the numbers \(\displaystyle \big(3-\sqrt{5}\,\big)\), \(\displaystyle \Big(\frac{3\sqrt{5}}{5}-q\Big)\), \(\displaystyle \Big(0,6-\frac{1}{\sqrt{5}}\Big)\) form a geometric progression?
(5 pont)
 |
Problems with sign 'B'Deadline expired on October 12, 2015. |
B. 4723. Are there infinitely many difference prime numbers, such that the sum of any 2015 of them is a composite number?
Proposed by G. Mészáros, Budapest
(3 pont)
B. 4724. Solve the inequality \(\displaystyle x+y-xy+\frac{1}{x} +\frac{1}{y} -\frac{1}{xy}\le 2 \) and represent it in the coordinate plane.
(4 pont)
B. 4725. Show that if a simple graph has 7 vertices and no cycle of length 4 then it has a vertex whose degree is at most 2.
(4 pont)
B. 4726. In a square \(\displaystyle ABCD\), points \(\displaystyle P\) and \(\displaystyle Q\) lie on sides \(\displaystyle AB\) and \(\displaystyle BC\), respectively, and \(\displaystyle BP = BQ\). Let \(\displaystyle T\) denote the foot of the perpendicular dropped from vertex \(\displaystyle B\) to the line segment \(\displaystyle PC\). Prove that \(\displaystyle \angle DTQ\) is a right angle.
(4 pont)
B. 4727. Determine all functions \(\displaystyle f:\mathbb R \to \mathbb R\) such that \(\displaystyle f(x+y)+f(x)f(y)=x^2 y^2+2xy\) for all \(\displaystyle x\) and \(\displaystyle y\).
(5 pont)
B. 4728. Let \(\displaystyle e\) be the line of one of the edges of a cube. How many lines of the space intersect exactly those out of the 12 lines containing the edges of the cube which are skew relative to \(\displaystyle e\)?
(3 pont)
B. 4729. A given quadrilateral \(\displaystyle ABCD\) has right angles at \(\displaystyle C\) and at \(\displaystyle D\). Construct that point \(\displaystyle P\) of line segment \(\displaystyle CD\) for which \(\displaystyle \angle APD = 2\angle BPC\).
(5 pont)
B. 4730. The circles \(\displaystyle k_1\) and \(\displaystyle k_2\) touch at point \(\displaystyle E\). Points \(\displaystyle X_i\) and \(\displaystyle Y_i\) are marked on each circle \(\displaystyle k_i\) (\(\displaystyle i = 1,2\)) such that the two lines \(\displaystyle X_iY_i\) intersect each other on the common interior tangent of the circles. Prove that the line connecting the centres of circles \(\displaystyle X_1X_2E\) and \(\displaystyle Y_1Y_2E\), and the other line connecting the centres of circles \(\displaystyle X_1Y_2E\) and \(\displaystyle X_2Y_1E\) also intersect each other on the common interior tangent of the circles.
Proposed by K. Williams, Szeged
(5 pont)
B. 4731. Let \(\displaystyle 0\le a,b,c \le 2\), and \(\displaystyle a+b+c=3\). Determine the largest and smallest values of
\(\displaystyle \sqrt{a(b+1)} + \sqrt{b(c+1)} + \sqrt{c(a+1)}. \)
Proposed by K. Williams, Szeged
(6 pont)
 |
Problems with sign 'A'Deadline expired on October 12, 2015. |
A. 647. Let \(\displaystyle k\) be a nonnegative integer. Prove that there are only finitely many positive integers \(\displaystyle n\) for which there exist two disjoint sets \(\displaystyle A\) and \(\displaystyle B\) satisfying \(\displaystyle A \cup B = \{1; 2; \ldots; n\}\) and \(\displaystyle \displaystyle\left|\prod \limits_{a \in A} {a} - \prod\limits _{b \in B} {b}\right|=k\).
Proposed by: Balázs Maga, Budapest
(5 pont)
A. 648. In the acute angled triangle \(\displaystyle ABC\), the midpoints of the sides \(\displaystyle BC\), \(\displaystyle CA\) and \(\displaystyle AB\) are \(\displaystyle D\), \(\displaystyle E\) and \(\displaystyle F\), respectively. The foot of the altitude of the triangle starting from \(\displaystyle C\) is \(\displaystyle T_1\). On some line, passing through point \(\displaystyle C\) but not containing \(\displaystyle T_1\), the feet of the perpendiculars starting from \(\displaystyle A\) and \(\displaystyle B\) are \(\displaystyle T_2\) and \(\displaystyle T_3\), respectively. Prove that the circle \(\displaystyle DEF\) passes through the center of the circle \(\displaystyle T_1T_2T_3\).
Proposed by: Bálint Bíró, Eger
(5 pont)
A. 649. A convex polyhedron has only quadrilateral faces. Show that it is possible to split every face into two triangles by drawing one of its diagonals in such a way that at each vertex of the polyhedron, an even number of triangles meet.
Proposed by: János Nagy, Budapest
(5 pont)
Upload your solutions above.
