KöMaL Problems in Informatics, December 2015
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'I'Deadline expired on January 11, 2016. |
I. 388. It is only since a few centuries that maps have been oriented in a way such that north is put on top. Earlier, various other directions were chosen to be put on top, depending on the cultural environment. Some Egyptian maps, for example, used the flow direction of the Nile river; American settlers used maps with west on top (the direction they were often heading); and in Europe, they put north on top.
In this exercise all maps are oriented according to one of the four cardinal directions. The maps were made to serve different purposes, and they have different cardinal points. By knowing the coordinates of these points, you need to determine the map orientation. The location of the origin can vary from map to map.
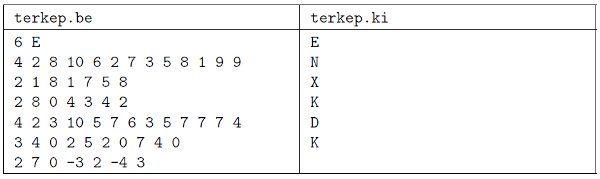
The first line of the input file (terkep.be) contains the number of maps (\(\displaystyle T\le 50\)), a space character as a separator, and the orientation of the first map (E, K, D, N, denoting north, east, south and west, respectively). Then each of the next \(\displaystyle T\) lines contains the following information. The first number is the number of points (\(\displaystyle N\)) on the given map; then there are \(\displaystyle N\) triplets: the first number in each triplet is the identification number of the actual point, then its \(\displaystyle X\) and \(\displaystyle Y\) coordinates (relative to the given map) appear. Each piece of data is separated by a space character. The total number of points is at most 50. The coordinate values lie in the interval \(\displaystyle [-1000; 1000]\) for a given orientation, however, by taking the union of some maps, this interval may become wider.
The output file (terkep.ki) should have exactly \(\displaystyle N\) lines; each line should have one character, the orientation of the actual map. If the orientation cannot be determined, a character X should be present in that line.
The source code and documentation of your program-containing a brief description of your solution, and the name of the developer environment to compile your code-should be submitted in a compressed file i388.zip.
(10 pont)
I. 389. Women's heptathlon is a combined athletics event. This has been the topic of our database management problem I. 338. Now you should evaluate the results of a similar event by using a spreadsheet application.
The seven events of a heptathlon are the following: 100 meters hurdles, 200 meters and 800 meters track running, high jump, long jump, shot put, and javelin throw. Points are awarded based on a specific formula and on an international standard performance table according to the following.
\(\displaystyle \text{Points obtained}=\big[A\cdot {|X-B|}^C\big], \)
where \(\displaystyle X\) is the athlete's performance, \(\displaystyle [~]\) denotes the integer part, and \(\displaystyle |~|\) is the absolute value. The constants \(\displaystyle A\), \(\displaystyle B\) and \(\displaystyle C\) are determined by the International Association of Athletics Federations, and depend on the type of the event:
|
The tabulator-separated and UTF-8-encoded file hetforras.txt contains data corresponding to the heptathlon events during the 2012 Summer Olympics, and the constants from the previous table.
1. Import the text file hetforras.txt into the spreadsheet application beginning with cell A1. (The range A1:I4 contains the transpose of the above table.) The name of the sheet should be eredmények (=results). Your work should be saved as hetproba (=hepathlon) in the default file format of the spreadsheet application.
2. Create a new sheet pontszámok (=scores), and create a header in the first row according to the sample.

3. In the range A2:B40 of this sheet-referencing cells A7:B45 of the sheet eredmények-display the name (=Név) and nationality (=Nemzet) of the 39 athletes.
4. In cells C2:I40, according to the method described above and by using a single formula and its copied version, you should determine the points for each athlete and for each event. If the corresponding eredmények cell is empty, then the referencing pontszámok cell should also be empty.
5. In cells J2:J40, for each athlete, you should give the sum of the points obtained for the events-provided that they have results in all seven categories; otherwise, a message ``Nincs'' (=none) should appear.
The following tasks should be solved by using the sheet eredmények.
6. In cell M2 and by using a function, you should determine the number of athletes who completed the heptathlon (=Versenyt teljesítők száma), that is, having points in all seven categories.
7. In cells K8:N17 and by using a formula, you should list the number of points (=Összpont), the name of the athlete (=Név), and the abbreviation of their nationality (=Nemzet) for the first 10 athletes (ranked according to their points (=Helyezés), which can be assumed to be different for different athletes).
8. In cells C50:I50, determine the names of the winners for each event. If there is a tie in a particular category, it is sufficient to give only one athlete name. 9. It is possible that more athletes participate in the heptathlon (=Résztvevők) from the same nation (=Nemzet). Under the cells K20:L20, you should list the number of athletes (sorted in decreasing order) for each nation. In column K in your solution, you can collect and use the 3-letter abbreviations of the nations-it is not required to use any formula. 10. Cells of the sheet eredmények should be formatted according to the sample sheet.
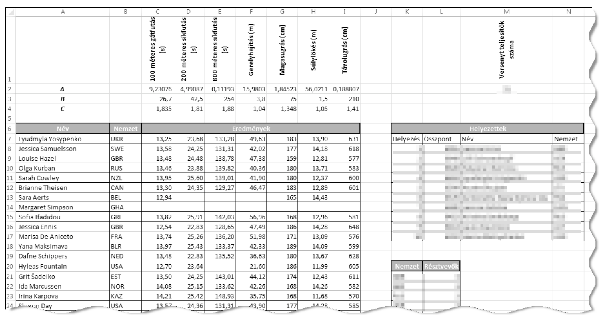
The spreadsheet (hetproba.xlsx, hetproba.odt) and a short documentation (also with the name and version number of the spreadsheet application) should be submitted in a compressed file i389.zip.
Downloadable file: hetforras.txt
(10 pont)
I. 390. Mobile apps-including various games-are getting more and more popular. One can make an app by using some free developer tools available under the three most popular mobile operating systems. Your task is to create a mobile app to play the following logic game.
The board consists of \(\displaystyle N\times N\) squares arranged in a grid; the two sides of each square have different colors (there are two colors altogether). If the player touches a square, its 4 neighbors (but not the actual square) will turn over, that is, their color will change to the opposite. The player wins when all squares have the same color. At the beginning of the game, the player should be able to set the board size (\(\displaystyle 3\le N\le 12\)); the application then should generate a random board coloring from which a final unicolor state can be reached. The executable version of your app (for Android, iOS or Windows Phone) and its full source, together with the web address of the chosen developer toolkit and a brief description of your steps designing the app, should be submitted in a compressed file (i390.zip).
(10 pont)
 |
Problems with sign 'I/S'Deadline expired on January 11, 2016. |
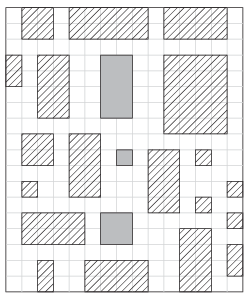
I/S. 4. Someone placed \(\displaystyle K\) (\(\displaystyle 0\le K\le 10\;000\)) boxes in a rectangular area of size \(\displaystyle N\times M\) (\(\displaystyle 10\le N, M\le 100\;000\)). Each box has unit height, but their width and length can vary. The sides of the boxes are parallel to the sides of the rectangle. The boxes do not touch each other, and they cannot be observed from above-only from the side-because they have been covered.
Your program is4 should determine the number of boxes that cannot be seen even if we examine the rectangle from all four directions. To spot a box, it is enough to see a part of its face. We can look into the rectangle only perpendicularly to one of its side, and in a straight line.
In the example, the striped boxes are visible, and the gray ones are invisible from outside.
Your program should read the values of \(\displaystyle N\), \(\displaystyle M\) and \(\displaystyle K\) from the first line of the standard input, then-from the following \(\displaystyle K\) lines-the \(\displaystyle X\) and \(\displaystyle Y\) coordinates (positive integers) of the upper left and lower right vertices of the boxes. The first and only line of the standard output should contain the number of invisible boxes. Your program should solve this task within 1 second of running time.

The source code and documentation of your program-containing a brief description of your solution, and the name of the developer environment to compile your code-should be submitted in a compressed file is4.zip.
(10 pont)
 |
Problems with sign 'S'Deadline expired on January 11, 2016. |
S. 103. There are \(\displaystyle N\) towns in a country. Your task is to design a road network such that one can travel between any two towns in exactly one way. The cost of building a particular road segment is directly proportional to its length, so we would like to minimize the total length of the network. However, there are also some hills in the country, making it impossible to build a road between any two arbitrary towns: it is only allowed to construct certain \(\displaystyle M\) roads specified by the input data. Moreover, due to some technical restrictions, the construction company cannot build more than three roads of a given length, hence the network should be designed such that there are at most three roads of any given length. Your program should determine the number of ways the network with the minimum total length can be built.
Your program should read the values of \(\displaystyle N\) and \(\displaystyle M\) (\(\displaystyle 1\le N \le 50\;000\), \(\displaystyle 1\le M\le 200\;000\)) from the first line of the standard input; then the \(\displaystyle a_i\), \(\displaystyle b_i\) and \(\displaystyle c_i\) integers (separated by a space) from the following \(\displaystyle M\) lines, representing the fact that a two-way road can be built from town \(\displaystyle a_i\) to town \(\displaystyle b_i\) with cost \(\displaystyle c_i\) (\(\displaystyle 1\le c_i\le 1\;000\;000\)). The first and only line of the standard output should contain the minimum total length of a valid network, moreover, the remainder on division of the number of possible networks by \(\displaystyle 1\;000\;000\;007\).

Explanation: The minimum total length is achieved if we choose the edges of length 1 and one edge of length 2.
Scoring and bounds. You can get 1 point for a brief and proper documentation clearly describing your solution. Nine further points can be obtained provided that your program solves any valid input within 1 second of running time.
The source code of your program and a short documentation-also describing which developer environment to use for compiling the source-should be submitted in a compressed file s103.zip.
(10 pont)
$Var(Body)
Upload your solutions above
