KöMaL Problems in Mathematics, December 2015
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on January 11, 2016. |
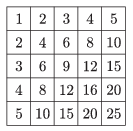
K. 481. What is the sum of the numbers in the \(\displaystyle 20\times 20\) multiplication table? (The figure shows the \(\displaystyle 5\times 5\) multiplication table.)
(6 pont)
K. 482. In a bicycle factory, the bicycles produced are tested systematically. The brakes are tested on every fifth bike, the gears are tested on every fourth, and the shifter is tested on every seventh one. They manufacture 435 bicycles a day. How many bicycles are issued from the factory per day without anything tested on them?
(6 pont)
K. 483. In how many different ways is it possible to write the numbers 1, 2, 3, 4, 5, 6, 7, 8, 9 on the circumference of a circle so that no sum of adjacent numbers is a multiple of 3, 5 or 7?
(6 pont)
K. 484. Every natural number 1 to \(\displaystyle n\) is written on a card. What is the smallest \(\displaystyle n\) such that no matter how the cards are divided into two packs, there will always be two cards in one of the packs with two numbers that add up to a perfect square?
(6 pont)
K. 485. Tom Thumb and the giant arrive at the castle of the dragon. Although the giant is 3.5 metres taller than Tom, he still cannot reach the top of the castle wall when he stands on the ground. So he lifts Tom Thumb on his palm over his head. Tom can just climb the wall, which is 6 metres and 20 centimetres high. The giant has long hands: he can reach 40% of his height above the top of his head, while Tom can only reach 20% of his height above the top of his head. How tall is the giant, and how tall is Tom Thumb?
(6 pont)
K. 486. How many five-digit positive numbers are there in which the sum and the product of the digits are both even?
(6 pont)
 |
Problems with sign 'C'Deadline expired on January 11, 2016. |
C. 1322. Three consecutive terms of an arithmetic progression of positive integers are written down in a row to form a single number. Find the largest seven-digit number obtained in this way.
Quantum, 1998
(5 pont)
C. 1323. Let \(\displaystyle T\) denote the intersection of side \(\displaystyle BC\) with the angle bisector drawn from vertex \(\displaystyle A\) of a right-angled triangle. Let \(\displaystyle F\) denote the midpoint of side \(\displaystyle BC\), and let \(\displaystyle M\) be the intersection of the perpendicular bisector drawn at \(\displaystyle F\) with another side. Given that the quadrilateral \(\displaystyle ATFM\) is a kite, determine the angles of the triangle. (\(\displaystyle A\) may denote any vertex of the triangle.)
(5 pont)
C. 1324. Agnes is making gingerbread hearts for Christmas. The pastry cutter has the shape of a 6 cm by 6 cm square with two semicircles attached to two adjacent sides. She always rolls the dough the same thickness, forming a square whose side is a whole number of decimetres. (If any dough remains, she gives it to her sister.) She starts cutting the hearts out of the pastry by placing the corner of the cutter to the corner of the pastry square, carefully aligning the sides. Then she continues by placing the cutter next to the cut-out squares with the same orientation, as close as possible. How many squares can Agnes make if she starts out with a 1 m\(\displaystyle {}^2\) pastry, and she always kneads together the pastry remaining after cutting out the hearts?
(5 pont)
C. 1325. Let \(\displaystyle a_n\) denote the closest integer to \(\displaystyle \sqrt n\). Determine the sum \(\displaystyle \frac 1{a_1}+ \frac 1{a_2}+ \frac 1{a_3}+\ldots + \frac 1{a_{484}}\).
(5 pont)
C. 1326. The perimeter of a right-angled trapezoidal plot is 400 m. One leg of the right angled trapezium makes an angle of \(\displaystyle 45^\circ\) with the base. For what length of the base would the area of the plot be a maximum?
(5 pont)
C. 1327. With line segments drawn from an interior point, dissect an octagon with the properties shown in the diagram into four parts, such that the parts can be put together to form two congruent regular pentagons.
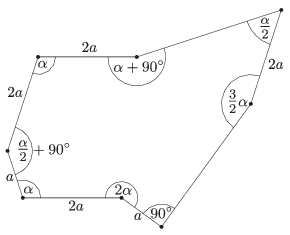
(5 pont)
C. 1328. Solve the following equation: \(\displaystyle 2^{\sin^2 x}= \frac{\sin x + \cos x}{\sqrt2}\).
(5 pont)
 |
Problems with sign 'B'Deadline expired on January 11, 2016. |
B. 4750. Ann claims that a random three-digit number is more likely to contain a digit of 6 than a random five-digit number. Bill says it is the other way around. Who is right?
Matlap, Kolozsvár
(3 pont)
B. 4751. Prove that \(\displaystyle 3^{n}+5^{n}\) is not a perfect square for any positive integer \(\displaystyle n\).
Proposed by G. Somlai, Budapest
(4 pont)
B. 4752. Consider circles \(\displaystyle k_1\) with center \(\displaystyle O_1\) and radius \(\displaystyle r_1\), and \(\displaystyle k_2\) with center \(\displaystyle O_2\) and radius \(\displaystyle r_2\). Line \(\displaystyle PA\) is tangent to \(\displaystyle k_1\) at \(\displaystyle A\) and line \(\displaystyle PD\) is tangent to \(\displaystyle k_2\) at \(\displaystyle D\). Segment \(\displaystyle AD\) intersects \(\displaystyle k_1\) and \(\displaystyle k_2\) at \(\displaystyle B\) and \(\displaystyle C\), respectively. Find \(\displaystyle PA/PD\) in terms of \(\displaystyle r_1\) and \(\displaystyle r_2\) if \(\displaystyle AB=CD\).
M&IQ
(4 pont)
B. 4753. Prove that \(\displaystyle \sqrt{2x \sqrt{(2x+1) \sqrt{(2x+2) \sqrt{2x+3}}}} < \frac{15x+6}{8}\) for all \(\displaystyle x>0\).
Proposed by I. Deák, Székelyudvarhely
(5 pont)
B. 4754. Lines \(\displaystyle AD\), \(\displaystyle BD\) and \(\displaystyle CD\) passing through an interior point \(\displaystyle D\) of a triangle \(\displaystyle ABC\) intersect the opposite sides at \(\displaystyle A_{1}\), \(\displaystyle B_{1}\) and \(\displaystyle C_{1}\), respectively. The midpoints of the segments \(\displaystyle A_1B_1\), \(\displaystyle B_1C_1\) and \(\displaystyle C_1A_1\) are \(\displaystyle C_2\), \(\displaystyle A_2\) and \(\displaystyle B_2\), respectively. Show that the lines \(\displaystyle AA_{2}\), \(\displaystyle BB_{2}\) and \(\displaystyle CC_{2}\) are concurrent.
Proposed by Sz. Miklós, Herceghalom
(5 pont)
B. 4755. In a triangle \(\displaystyle ABC\), the escribed circles \(\displaystyle k_A\) and \(\displaystyle k_B\) drawn to sides \(\displaystyle CB\) and \(\displaystyle CA\) touch the appropriate sides at \(\displaystyle D\) and \(\displaystyle E\), respectively. Show that line \(\displaystyle DE\) cuts out equal chords from the circles \(\displaystyle k_A\) and \(\displaystyle k_B\).
Proposed by K. Williams, Szeged
(4 pont)
B. 4756. In the interior of a unit cube, there are some spheres with a total surface area of 2015. Show that
\(\displaystyle a)\) there exists a line that intersects at least 500 spheres,
\(\displaystyle b)\) there exists a plane that intersects at least 600 spheres.
Hungarian Mathematics Competition of Transylvania
(6 pont)
B. 4757. Let \(\displaystyle A_k\) denote the number that consists of \(\displaystyle k\) ones in decimal notation. How many positive integers are there that cannot be obtained as the sum of the digits of any multiple of \(\displaystyle A_k\)?
Proposed by K. Williams, Szeged
(6 pont)
B. 4758. What is the minimum number of different lines determined by the sides of a (not necessarily convex) 2015-sided polygon?
Proposed by D. Lenger, Budapest
(6 pont)
 |
Problems with sign 'A'Deadline expired on January 11, 2016. |
A. 656. Let \(\displaystyle p(x)=a_0+a_1x+\dots+a_nx^n\) be a polynomial with real coefficients such that \(\displaystyle p(x)\ge0\) for \(\displaystyle x\ge0\). Prove that for every pair of positive numbers \(\displaystyle c\) and \(\displaystyle d\), \(\displaystyle a_0 + a_1(c+d) + a_2(c+d)(c+2d) + \dots + a_n(c+d)(c+2d)\dots(c+nd) \ge0\).
(5 pont)
A. 657. Let \(\displaystyle \{x_n\}\) be the van der Korput sequence, that is, if the binary representation of the positive integer \(\displaystyle n\) is \(\displaystyle n = \sum_i a_i2^i\) (\(\displaystyle a_i\in\{0,1\}\)), then \(\displaystyle x_n = \sum_i a_i2^{-i-1}\). Let \(\displaystyle V\) be the set of points \(\displaystyle (n,x_n)\) in the plane where \(\displaystyle n\) runs over the positive integers. Let \(\displaystyle G\) be the graph with vertex set \(\displaystyle V\) that is connecting any two distinct points \(\displaystyle p\) and \(\displaystyle q\) if and only if there is a rectangle \(\displaystyle R\) which lies in a parallel position to the axes and \(\displaystyle R\cap V = \{p,q\}\). Prove that the chromatic number of \(\displaystyle G\) is finite.
Miklós Schweitzer competition, 2015
(5 pont)
A. 658. We call a bar of width \(\displaystyle w\) on the surface \(\displaystyle S^2\) of the unit sphere in \(\displaystyle 3\)-dimension, centered at the origin a spherical zone which has width \(\displaystyle w\) and is symmetric with respect to the origin. Prove that there exists a constant \(\displaystyle c>0\) such that for every positive integer \(\displaystyle n\) the surface \(\displaystyle S^2\) can be covered with \(\displaystyle n\) bars of the same width so that every point is contained in no more than \(\displaystyle c\sqrt{n}\) bars.
Miklós Schweitzer competition, 2015
(5 pont)
Upload your solutions above.
