KöMaL Problems in Mathematics, January 2016
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on February 10, 2016. |
K. 487. Find the largest and the smallest eight-digit numbers in which the digits are 0, 1, 2, 3, 4, 5, 6, 7 in some order, and the sum of every pair of adjacent digits is a prime.
(6 pont)
K. 488. Prove that if \(\displaystyle a \ge n\) where \(\displaystyle a\) and \(\displaystyle n\) are positive integers, then the product \(\displaystyle (a-1)(a-2)(a-3)\dots (a-n)\) is divisible by \(\displaystyle n\).
(6 pont)
K. 489. Peter entered the first 2015 positive integers in a \(\displaystyle 100\times 100\) table, as shown in the figure. (In the figure, the table is not filled in completely yet.) What is the last number in the second row?
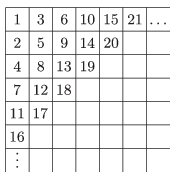
(6 pont)
K. 490. Anthony is training ants. The performance starts with 99 ants sleeping on a 1-metre long straight rod. When a whistle is blown, they all wake up at the same time, and start crawling towards an end of the rod, at a speed of 1 cm/s. If an ant reaches the end of the rod, it will leave the rod. If two ants meet, they will turn back immediately, and start crawling in the opposite direction. The performance ends when the last ant has left the rod. What is the maximum possible duration of the performance?
(6 pont)
K. 491. Andrew has chosen five numbers. He wrote them on a sheet of paper, and formed every possible sum of three terms out of them. He got the following results: 3, 4, 6, 7, 9, 10, 11, 14, 15 and 17. Which were the five original numbers that Andrew had in mind?
(6 pont)
K. 492. How many at most four-digit numbers are there in which the sum of the digits is at most 31?
(6 pont)
 |
Problems with sign 'C'Deadline expired on February 10, 2016. |
C. 1329. King Sanislaus sends an envoy to a distant empire. In three days, a courier is sent back to the King's court with a message. It takes the courier two days to cover the same distance as the envoy takes three days to cover. With the answer, the courier returns to the envoy, and catches up with them exactly as they arrive at the destination. However, the emperor, who is a great friend of king Sanislaus, has been exiled in the meantime, so the entire envoy returns immediately, and this time they all travel at the speed of the courier. How many days elapse between the envoy starting their journey and returning to the court?
(5 pont)
C. 1330. How many different rectangular mosaics can be made out of four different photos of \(\displaystyle 2:3\) aspect ratio? (The photos may be enlarged, but may not be rotated. Two mosaics are considered identical if they are obtained from each other by enlargement.)
(5 pont)
C. 1331. Pete invited 13 friends to the party celebrating his 13th birthday. He received 13 coloured candles from each friend. The candles were right cylinders of radius 2.5 cm and height 30 cm. In order to keep his treasures safe, Pete has got hold of a large rectangular box of dimensions \(\displaystyle \rm 50~cm \times 78~cm \times 31~cm\). Can he place all the candles in the box so that no candle should stick out of the box or be injured?
(5 pont)
C. 1332. Vicky's grandma buys one lottery ticket per week. What is the probability that she will not win at all during the course of a whole year (in 52 weekly draws)? (In the lottery, 5 numbers are drawn out of 90. A ticket will win if at least 2 are marked out of the five numbers drawn.)
(5 pont)
C. 1333. Find that set of three real numbers for which the mean, the median and the standard deviation are all 3.
(5 pont)
C. 1334. Given that the cyclic quadrilateral \(\displaystyle ABCD\) is either a trapezium (where \(\displaystyle AB\parallel CD\)) or its side \(\displaystyle AB\) is a diameter of the circumscribed circle, then the equations
\(\displaystyle BD\cdot x+AD\cdot \sqrt{1-x^2} = AC;\)
\(\displaystyle AC\cdot x+BC\cdot \sqrt{1-x^2} = BD\)
are held for some \(\displaystyle x\) of \(\displaystyle 0<x<1\).
(5 pont)
C. 1335. The base edges of a regular triangular pyramid have unit length, and the length of the lateral edges is 2. Find the distance between two skew edges.
(5 pont)
 |
Problems with sign 'B'Deadline expired on February 10, 2016. |
B. 4759. Four men and four women are sitting around a round table. Prove that there are four adjacent people such that there are the same number of men and women among them.
(3 pont)
B. 4760. Four regular dice of different colours are placed next to each other, as shown in the figure. In each step, two adjacent cubes (with a face in common) are turned through \(\displaystyle 90^\circ\) about the axis passing through the centre and perpendicular to the common face. How many different arrangements can be achieved with a sequence of such steps?
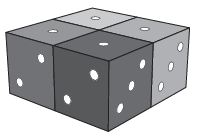
(6 pont)
B. 4761. Let \(\displaystyle n\) be an integer greater than 3. Prove that if each digit occurs exactly once in the base-\(\displaystyle n\) representation of an integer then the number cannot be a prime.
Proposed by Z. Halasi, Csobánka
(4 pont)
B. 4762. In a simple graph, the degree of each vertex is four, and for each edge there exists exactly one vertex connected to both ends of the edge. What is the minimum number of vertices in such a graph?
(3 pont)
B. 4763. Let \(\displaystyle G\) be a simple undirected graph of \(\displaystyle n\) vertices. Prove that it is possible to assign infinite sets \(\displaystyle \mathcal{H}_1,\mathcal{H}_2, \dots, \mathcal{H}_n\) of natural numbers to the graph such that the intersection of two sets is infinite if the corresponding vertices are joined by an edge, and empty if there is no edge joining the vertices.
Proposed by G. Mészáros, Budapest
(4 pont)
B. 4764. In the rectangular coordinate plane, consider all lines with equations of the form \(\displaystyle aX+\frac{Y}{a}=2\), where \(\displaystyle a\) is a real number. Determine the set of those points in the plane that do not lie on any of the lines.
(5 pont)
B. 4765. In a cyclic quadrilateral \(\displaystyle ABCD\), the angle bisectors of angles \(\displaystyle ADB\sphericalangle\) and \(\displaystyle ACB\sphericalangle\) intersect side \(\displaystyle AB\) at points \(\displaystyle E\) and \(\displaystyle F\), and the bisectors of \(\displaystyle CBD\sphericalangle\) and \(\displaystyle CAD\sphericalangle\) intersect side \(\displaystyle CD\) at \(\displaystyle G\) and \(\displaystyle H\), respectively. Prove that the points \(\displaystyle E\), \(\displaystyle F\), \(\displaystyle G\), \(\displaystyle H\) are concyclic.
Proposed by B. Bíró, Eger
(6 pont)
B. 4766. The sequence \(\displaystyle a_{1}, a_{2}, \dots\) is defined by the following recursion: \(\displaystyle a_{1}=1\), \(\displaystyle a_{2}=5\), \(\displaystyle a_{3}=15\), and in the case of \(\displaystyle n\ge 4\), \(\displaystyle a_{n}=n^{2}+a_{n-1}+a_{n-2}-a_{n-3}\).
\(\displaystyle a)\) Calculate the sum \(\displaystyle a_{1}+a_{2}+a_{3}+\dots +a_{2015}\).
\(\displaystyle b)\) Prove that \(\displaystyle \frac{1}{a_{1}}+\frac{1}{a_{2}}+\frac{1}{a_{3}}+ \dots +\frac{1}{a_{2015}}<\frac{4}{3}\).
Proposed by B. Kovács, Szatmárnémeti
(5 pont)
B. 4767. Find those convex polyhedra in which for each vertex \(\displaystyle C\), the angles lying at \(\displaystyle C\) on the faces meeting at \(\displaystyle C\) add up to \(\displaystyle 180^\circ\).
(6 pont)
 |
Problems with sign 'A'Deadline expired on February 10, 2016. |
A. 659. For which \(\displaystyle n\) are there polynomials \(\displaystyle g(x)\) and \(\displaystyle h(x)\) with real coefficients and degrees smaller than \(\displaystyle n\) such that \(\displaystyle g\big(h(x)\big)= x^n+x^{n-1}+x^{n-2}+\dots +x^2+x+1\)?
Miklós Schweitzer Competition, 2015
(5 pont)
A. 660. The circle \(\displaystyle \omega\) is inscribed in the quadrilateral \(\displaystyle ABCD\). The incenters of the triangles \(\displaystyle ABC\) and \(\displaystyle ACD\) are \(\displaystyle I\) and \(\displaystyle J\), respectively. Let \(\displaystyle T\) and \(\displaystyle U\) be those two points on the arcs of \(\displaystyle \omega\), lying in the triangles \(\displaystyle ABC\) and \(\displaystyle ACD\), respectively, for which the circles \(\displaystyle ATC\) and \(\displaystyle AUC\) are tangent to \(\displaystyle \omega\). Show that the line segments \(\displaystyle AC\), \(\displaystyle IU\) and \(\displaystyle JT\) are concurrent.
(5 pont)
A. 661. Let \(\displaystyle K\) be a fixed positive integer. Let \(\displaystyle (a_0,a_1,\dots)\) be the sequence of real numbers that satisfies \(\displaystyle a_0=-1\) and
\(\displaystyle \sum_{\substack{i_0,i_1,\dots,i_K\ge0 \\ i_0+i_1+\dots+i_K=n}} \frac{a_{i_1}\cdot\dots\cdot a_{i_K}}{i_0+1} =0 \)
for every positive integer \(\displaystyle n\). Show that \(\displaystyle a_n>0\) for \(\displaystyle n\ge1\).
(5 pont)
Upload your solutions above.
