KöMaL Problems in Physics, March 2016
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'M'Deadline expired on April 11, 2016. |
M. 358. By means of devices at home measure your vital capacity. (This is the maximum volume of air at atmospheric pressure which can be expelled from your lungs after a maximum inhalation.)
(6 pont)
 |
Problems with sign 'P'Deadline expired on April 11, 2016. |
P. 4818. Hansel and Gretel live at a distance of 250 metres from each other. They both leave the house at half past seven in the morning. Gretel walks at a speed of 1.1 m/s towards the school. Hansel - since he lives further - walks at a speed of 1.5 m/s. Hansel just catches up with Gretel at the school-gate. How far does Gretel live from the school? At what time did they enter the school?
(3 pont)
P. 4819. Half a litre of water is boiled by means of an immersion heater, rated at 500 W. How long does it take to increase the temperature of the 0.5 litres of water from \(\displaystyle 20~^\circ\)C to its boiling point, if the efficiency of heating is 80%? What may the reason be for the 20% loss of energy if the heat released by the immersion heater is totally absorbed by the water?
(3 pont)
P. 4820. The length of a metal wire of known resistivity can be measured with an accuracy of 0.1%, whilst its width can be measured with the accuracy of 2%. At what accuracy can
\(\displaystyle a)\) the volume and
\(\displaystyle b)\) the resistance of the wire be calculated?
(3 pont)
P. 4821. If a solid cork sphere of density 400 kg/m\(\displaystyle {}^3\) is suspended by a spring, then the elongation of the spring is 10 cm.
\(\displaystyle a)\) The sphere and the spring are both placed into a container which is filled with water, such that one end of the spring is attached to the bottom of the container, and the other is fixed to the cork sphere. The system is in equilibrium, the spring is stretched, and half of the cork sphere is immersed into the water. What is the elongation of the spring at this state?
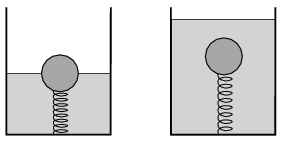
\(\displaystyle b)\) What will the elongation of the spring be, if more water is poured into the container, such that the whole cork sphere is immersed into the water?
(4 pont)
P. 4822. What should the angle between two forces be in order that their sum is equal to the
\(\displaystyle a)\) root-mean-square value of the magnitudes of the forces;
\(\displaystyle b)\) harmonic mean of the forces?
Under what conditions will these angles be minimal, and what are these minimum values?
(4 pont)
P. 4823. Two spheres (with uniform density) are placed to a fixed inclined plane of angle of elevation \(\displaystyle \alpha\) as shown in the figure. What can the angle \(\displaystyle \alpha\) be if it can be assumed that during the rolling motion of the spheres the line which joins the centres of the spheres remains vertical? What is the acceleration of the spheres in this case?
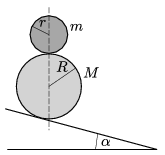
(Air drag is negligible, and the static friction is big enough.)
(5 pont)
P. 4824. The water of a lake in winter becomes colder and colder. Finally it freezes, and the width of the ice is getting thicker. Supposing that the air temperature is \(\displaystyle -20~{}^\circ\)C, sketch the graph of the temperature at a certain moment as the function of the depth measured from the top of the ice cover down to the bottom of the lake.
(4 pont)
P. 4825. A thermally insulated container is divided into two parts of volumes \(\displaystyle V\) and \(\displaystyle 2V\) by a thermally insulated piston. Initially both parts contain air at the temperature of \(\displaystyle T_0=300~\rm K\), and at the pressure of \(\displaystyle p_0=10^5~\rm Pa\). An electric heater of resistance \(\displaystyle R=100\,\Omega\), rated at \(\displaystyle U=230\) V, is built into that part which has a volume of \(\displaystyle V=2\) litres. The heater is operated until the values of the volume of the gas at the two parts ``swap over'', that is, in accordance with the figure the volume of the gas at the left hand-side of the container becomes \(\displaystyle V\), and the volume of the gas at the right hand-side becomes \(\displaystyle 2V\).
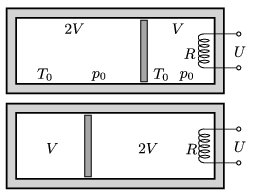
\(\displaystyle a)\) What are the temperature values at the two parts of the container at the end?
\(\displaystyle b)\) How long did the process take?
(5 pont)
P. 4826. The plates of a parallel plate condenser are charged to \(\displaystyle Q_1=2\cdot10^{-5}\) C, and \(\displaystyle Q_2=5\cdot10^{-5}\) C, and then an uncharged metal cuboid is inserted into the space between the plates of the condenser. Two faces of the cuboid are parallel to the plates of the condenser and they have the same area as the plates. What are the values of the charges on the surfaces of the left and right faces of the cuboid?
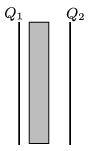
(4 pont)
P. 4827. Determine the currents in all the branches of the circuit shown in the figure.
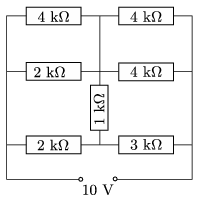
(4 pont)
P. 4828. The disc if radius \(\displaystyle r\), shown in the figure is made of some insulating material, and is rolling in uniform magnetic field without slipping along the horizontal ground at a constant speed of \(\displaystyle v\). The magnetic induction \(\displaystyle B\) is perpendicular to the plane of the disc. A thin copper rod of radius \(\displaystyle r\) joins the centre of the disc with the rim of the disc. Plot the induced electromotive force between the two ends of the copper rod as a function of the angle \(\displaystyle \alpha\), which is measured between the rod and the horizontal.
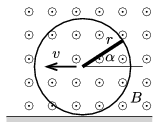
(4 pont)
P. 4829. Two stars of different masses \(\displaystyle m_1\) and \(\displaystyle m_2\) are moving in the gravitational field of each other, while there are no other forces exerted on them. At a certain moment the distance between them is \(\displaystyle d_0\), and their velocities (magnitude and direction) are such, as if they revolve about their common centre of mass at an angular speed of \(\displaystyle \omega_0\).
\(\displaystyle a)\) What is the maximum value of \(\displaystyle \omega_0\) if \(\displaystyle d_0\) is the greatest distance between the two stars, and what is the minimum value of \(\displaystyle \omega_0\) if \(\displaystyle d_0\) is the least distance between the two stars?
\(\displaystyle b)\) What is the value of \(\displaystyle \omega\) if the gravitational field cannot keep the system together?
\(\displaystyle c)\) What is the period when gravitation keeps the system together?
(6 pont)
Upload your solutions above.
