KöMaL Problems in Mathematics, March 2016
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on April 11, 2016. |
K. 499. Cats are chasing mice. Five mice hide in a crack of the wall. Then there are twice as many cats as running mice. Now ten cats get bored of the race and stop. Then there are three times as many mice running as cats chasing them. How many mice and how many cats started the chasing game?
(6 pont)
K. 500. In the ballroom, there are five girls and five boys who would like to waltz. Ann is 160 cm tall, Beth is 165, Carol is 166, Dora is 168 and Emily is 170. Frank is 166 cm tall, Gabe is 168, Hugh is 169, Ian is 172, and Jack is 178. In how many different ways can they form dancing couples if a girl will only dance with a boy if he is taller than herself?
(6 pont)
K. 501. Given the points \(\displaystyle A\) and \(\displaystyle B\), and a line \(\displaystyle e\) in a plane, with \(\displaystyle e\) passing at a distance of 2 cm from \(\displaystyle A\) and a distance of 3 cm from \(\displaystyle B\). Determine the number of appropriate lines \(\displaystyle e\) as a function of the distance \(\displaystyle AB\).
(6 pont)
K. 502. In a school trip, we asked each participant how many classmates of his or hers were present. Every student answered the question. Ten of them said 4, twelve said 3, six said 2, and four said 1. The class teacher of every child was also there and no other teachers took part in the trip. How many students and how many teachers were present in the school trip?
Proposed by L. Lorántfy, Dabas
(6 pont)
K. 503. A mathematics teacher was having fun on the 1st of April. During that day, he interpreted any written numbers and operations as representations in the base equal to the whole hour of the time instant the operation was carried out. (For example, at 32 minutes past 1 p.m., that is, at 13:32, he assumed that numbers were represented in base 13.) When he first carried out a multiplication, he got 181 as a result. One hour later, he carried out the multiplication written down with the very same digits, and got 180. Two additional hours after the second multiplication, he added the numbers 180 and 181, and obtained 341. What was the original multiplication (written down with the original digits)?
(6 pont)
K. 504. Calculate the circumference of the polygon shown in the figure.
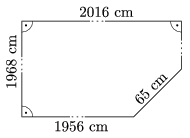
(6 pont)
 |
Problems with sign 'C'Deadline expired on April 11, 2016. |
C. 1343. At present, a father is five years older than the total age of his three sons. In ten, twenty, and thirty years, the father's age will be twice the age of his first, second and third son, respectively. How old is the father now, and how old are his sons?
(Matlap)
(5 pont)
C. 1344. Show that the difference between the longest and shortest diagonals of a regular nonagon equals the length of the side.
(5 pont)
C. 1345. How many of the first \(\displaystyle 3^n\) positive integers can be expressed as a sum of different powers of 3?
(5 pont)
C. 1346. Two line segments are drawn from a vertex of a unit square to cut the square into three parts of equal area: two triangles and a kite enclosed between them. The procedure is repeated with an adjacent vertex. What is the area of the intersection of the two kites?
(5 pont)
C. 1347. Is it possible to glue together some small cubes of \(\displaystyle 1~\rm cm^3\) volume such that the resulting solid is not hollow, and its volume \(\displaystyle V\) in \(\displaystyle \rm cm^3\) and surface area \(\displaystyle A\) in \(\displaystyle \rm cm^2\) satisfy \(\displaystyle V=\frac{5}{4}A\)?
(5 pont)
C. 1348. In a triangle, the measures of the sides are consecutive integers, and the largest angle is twice the smallest angle. How long are the sides?
(5 pont)
C. 1349. Charlie and his friends like playing poker dice. Charlie decided to play a prank on his friends, and on one of the five dice he eliminated the central dots of the faces with 3 and 5 dots. Now that die shows one 1, two 2's, two 4's and one 6. The next time they played, no one noticed the trick.
If one rolls the five dice prepared in this way, what is the probability that at least four identical numbers will appear on top?
(5 pont)
 |
Problems with sign 'B'Deadline expired on April 11, 2016. |
B. 4777. There are three species of creatures peopling the planet B-4777: the Alpha, the Beta and the Gamma. People of one species (not necessarily the Alpha) have 2 hands, people of another species have 3 hands, and people of the third species have 4 hands. People of one species (not necessarily those with 2 hands) have 4 fingers on each hand, people of another species have 5, and people of the third species have 6 hands on each hand. Every people represent numbers in a notation with a base equal to the total number of fingers on their hands. (For example, if those with 4 hands have 6 fingers on each, then they will use base-24 representation.) The number \(\displaystyle 64_{\alpha}\) expressed in the notation of the Alpha people coincides with the number \(\displaystyle 51_{\beta}\) expressed in the notation of the Beta people. How many hands and how many finger per hand do the Alpha, the Beta and the Gamma have?
Proposed by A. Sztranyák, Budapest
(3 pont)
B. 4778. Let \(\displaystyle D\) denote an interior point of an acute-angled triangle \(\displaystyle ABC\). Construct the circles of diameters \(\displaystyle AD\), \(\displaystyle BD\) and \(\displaystyle CD\), and draw a tangent from each of the points \(\displaystyle A\), \(\displaystyle B\) and \(\displaystyle C\) to each of the two circles not passing through it. Prove that the sum of the squares of the six tangents equals the sum of the squares of the sides of the triangle.
(3 pont)
B. 4779. The two points dividing side \(\displaystyle AB\) of triangle \(\displaystyle ABC\) into three equal parts, and the two points dividing side \(\displaystyle BC\) in a 1 to 3 ratio form a cyclic quadrilateral. The circumscribed circle of the quadrilateral is tangent to side \(\displaystyle CA\). Determine the angles of triangle \(\displaystyle ABC\).
(4 pont)
B. 4780. For what natural numbers \(\displaystyle n\) is it true that whenever the midpoints of the sides of a convex \(\displaystyle n\)-sided polygon \(\displaystyle \mathcal{K}_n\) form a regular \(\displaystyle n\)-gon, then \(\displaystyle \mathcal{K}_n\) itself is also a regular \(\displaystyle n\)-gon?
(4 pont)
B. 4781. The rows and the columns of an \(\displaystyle n \times n\) chessboard are numbered 1 to \(\displaystyle n\), and a coin is placed on each field. The following game is played: A coin showing tails is selected. If it is in row \(\displaystyle k\) and column \(\displaystyle m\), then every coin with row number at least \(\displaystyle k\) and column number at least \(\displaystyle m\) is turned over. This procedure is repeated.
What is the least number \(\displaystyle L(n)\) for which it is possible to achieve in at most \(\displaystyle L(n)\) steps that all coins on the board show heads, whatever be the initial distribution of heads and tails?
Proposed by D. Lenger, J. Szoldatics, Budapest
(6 pont)
B. 4782. Solve the following equation on the set of real numbers:
\(\displaystyle 8^x+27^x+2\cdot30^x+54^x+60^x= 12^x+18^x+20^x+24^x+45^x+90^x. \)
Proposed by B. Kovács, Szatmárnémeti
(4 pont)
B. 4783. A flea is jumping on the vertices of a square \(\displaystyle ABCD\). It starts at vertex \(\displaystyle A\), and in each jump he moves to an adjacent vertex with a probability of \(\displaystyle \frac{1}{2}\) for each. The flea will stop when it has reached all vertices at least once. For each vertex, determine the probability of its being the last vertex.
(5 pont)
B. 4784. Prove that the following inequality is true for all real numbers \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\):
\(\displaystyle 2\big(a^4+b^4+c^4\big)+\frac{71+17\sqrt{17}}{2}\ge 4abc+ a^2b^2+c^2a^2+3b^2c^2. \)
Proposed by M. Sawhney, Commack, NY, USA
(6 pont)
B. 4785. \(\displaystyle \mathcal{G}\) is a given sphere in the space. For any line \(\displaystyle e\) that has no common point with \(\displaystyle \mathcal{G}\), define the line \(\displaystyle f\) as the conjugate of \(\displaystyle e\) with respect to \(\displaystyle \mathcal{G}\) if \(\displaystyle f\) joins the points of tangency on the two planes tangent to \(\displaystyle G\) passing through \(\displaystyle e\). Show that two lines of the space passing \(\displaystyle \mathcal{G}\) are skew if and only if their conjugates with respect to \(\displaystyle \mathcal{G}\) are skew.
(5 pont)
 |
Problems with sign 'A'Deadline expired on April 11, 2016. |
A. 665. Let \(\displaystyle a_1,a_2,\ldots,a_n\) be distinct positive integers. Show that
\(\displaystyle 3\sum_{i=1}^{n}a_i^5+\bigg(\sum_{i=1}^{n}a_i\bigg)^{2} \ge 4\bigg(\sum_{i=1}^{n}a_i^3\bigg)\bigg(\sum_{i=1}^{n}a_i\bigg). \)
Proposed by: Mehtaab Sawhney, Commack, USA
(5 pont)
A. 666. Let \(\displaystyle p\) be a prime, let \(\displaystyle k\) be a positive integer, and let \(\displaystyle \mathcal{A}\) be a finite set of integers with at least \(\displaystyle p^k\) elements. Denote by \(\displaystyle N_{\text{even}}\) the number of subsets of \(\displaystyle \mathcal{A}\) with even cardinality and sum of elements being divisible by \(\displaystyle p^k\). Similarly, denote by \(\displaystyle N_{\text{odd}}\) the number of subsets of \(\displaystyle \mathcal{A}\) with odd cardinality and sum of elements being divisible by \(\displaystyle p^k\). Show that \(\displaystyle N_{\text{even}}\equiv N_{\text{odd}} \pmod{p}\).
(5 pont)
A. 667. On the circumcircle of the scalene triangle \(\displaystyle ABC\), let \(\displaystyle A_0\), \(\displaystyle B_0\), and \(\displaystyle C_0\) be the midpoints of the arcs \(\displaystyle BAC\), \(\displaystyle CBA\) and \(\displaystyle ACB\), respectively. Denote by \(\displaystyle A_1\), \(\displaystyle B_1\) and \(\displaystyle C_1\) the Feuerbach points of the triangles \(\displaystyle AB_0C_0\), \(\displaystyle BC_0A_0\) and \(\displaystyle CA_0B_0\), respectively. Show that the triangles \(\displaystyle A_0B_0C_0\) and \(\displaystyle A_1B_1C_1\) are similar.
Russian problem
(5 pont)
Upload your solutions above.
