KöMaL Problems in Physics, May 2016
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'M'Deadline expired on June 10, 2016. |
M. 360. Carefully place a water drop to a dry horizontal plastic sheet. Tilting the sheet, slowly increasing its angle of elevation, at some critical angle the water drop suddenly begins to move down the slope.
Measure how the critical angle depends on the mass of the water drop. Investigate the phenomenon in case of different types of plastic sheet.
(6 pont)
 |
Problems with sign 'P'Deadline expired on June 10, 2016. |
P. 4843. A vertical plane mirror is rotating uniformly about a vertical axis, completing 300 rotations in each minute. A horizontal beam of laser light is incident on the mirror.
Determine the angular speed of the reflected beam.
(3 pont)
P. 4844. From a boat stones of total volume \(\displaystyle 0.5~\mathrm{m}^3\), and of density \(\displaystyle 2400~\mathrm{kg/m}{}^3\) is dropped into the water of a lake. Due to this the water level of the lake decreases by 1.7 mm (after the waves are ceased).
What is the surface area of the lake?
(3 pont)
P. 4845. There is an object of mass \(\displaystyle m_2=1\) kg at rest on the top of a cart of mass \(\displaystyle m_1=2\) kg. Between the object and the wall of the cart at its back there is a spring kept tight with a piece of thread as shown in the figure. After burning the thread the spring pushes the 1 kg object off the cart at a speed of 6 m/s with respect to the ground.
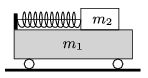
How much elastic potential energy was stored in the spring? (Friction is negligible.)
(3 pont)
P. 4846. An equilateral triangle is cut from a uniform sheet. The triangle is hung at one point \(\displaystyle P\) at its rim. The distance between point \(\displaystyle P\) and one of the vertices of the triangle is \(\displaystyle x\) times the side of the triangle.
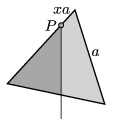
The vertical line through point \(\displaystyle P\) cuts the triangle into two parts. What is the ratio of the masses of these two parts? When will this ratio have an extremum and what is this extremum?
(5 pont)
P. 4847. Ond is on holiday at the beach of an equilateral triangle shaped lake. Once, when he is standing 10 m from the water of the lake exactly at one of the symmetry axis of the triangle, he catches the sight of Kond sunbathing at one of the other sides of the lake. Ond's and Kond's positions are symmetrical. What should the path of Ond be in order that he reaches his friend at the shortest time, if his overland speed is 10 km/h and his speed in the water is 2 km/h?
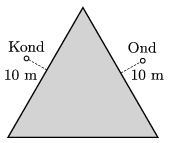
(4 pont)
P. 4848. A cart can move frictionlessly along a long inclined plane. The cart is given an initial velocity parallel to the slope, and then a bit later it is suddenly stopped. At most how long did the motion of the cart last, if during the last second of the motion it moved half of the distance covered during the whole motion?
(5 pont)
P. 4849. The total mass of an easily moveable cart and a hemisphere shaped container of radius \(\displaystyle R=0.3\) m attached to the cart is \(\displaystyle M=2\) kg. Initially a point-like object of mass \(\displaystyle m=1\) kg is held at the rim of the hemisphere (such that it touched the rim), and then it is released from rest.
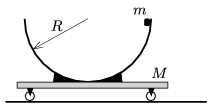
\(\displaystyle a)\) What are the velocities of the small object and the cart when the object descended a height of \(\displaystyle h=R/2\)? (Give both directions and speeds.)
\(\displaystyle b)\) What is the radius of the curvature of the path of the motion of the object with respect to the ground, when it reaches its lowest position? (Friction is negligible everywhere.)
(5 pont)
P. 4850. The mass of a small ball is 5 g, and its diameter is 4 cm. The ball is hit upward at a speed of \(\displaystyle 10~\frac{\rm m}{\rm s}\) in the air which has a temperature of \(\displaystyle 20~{}^\circ\)C and a pressure of 1 bar. Calculate with approximations the followings:
\(\displaystyle a)\) the height to which the ball ascends;
\(\displaystyle b)\) the time during which the ball arrives back to its initial position;
\(\displaystyle c)\) the speed of the ball when it gets back to its initial position.
(6 pont)
P. 4851. In aerodynamics the Mach number is the ratio of the speed of the object moving in air and the local speed of sound.
During a fighter aircraft training one of the fighters ascends from a region of \(\displaystyle 0~{}^\circ\)C air at a height of some kilometres, while its speed increases from 1.5 Mach to 1.75 Mach. Due to the jet powered engine the fighter's kinetic energy increased by 20%, and its mass decreased by 1%.
\(\displaystyle a)\) What is the temperature of the air (in \(\displaystyle {}^\circ\)C) at the height to which the fighter moved?
\(\displaystyle b)\) How much did the fighter ascend, and what is its final speed if the temperature of the air decreases \(\displaystyle 0.65~{}^\circ\) in each 100 m increase in height?
(5 pont)
P. 4852. There is a frictionlessly moveable piston in a thermally insulated vertical cylinder closed at both of its ends and of cross section \(\displaystyle A=1~{\rm dm}^2\). Two springs (which are both designed for compression and tension) are attached to the piston and to the two bases of the cylinder. The unstretched lengths of the springs are \(\displaystyle \ell_1=3~{\rm dm}\) and \(\displaystyle \ell_2=5~{\rm dm}\), whilst their spring constants are \(\displaystyle D_1=1000\) N/m and \(\displaystyle D_2=1500\) N/m. Bellow the piston there is air, the pressure of which initially is \(\displaystyle p_1=4\cdot10^4\) Pa, whilst above the piston there is vacuum. Initially the distances between the piston and the bases of the cylinder are \(\displaystyle d_1=5~{\rm dm}\) and \(\displaystyle d_2=4~{\rm dm}\).
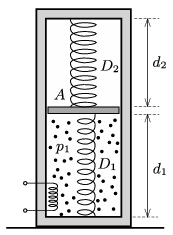
\(\displaystyle a)\) Determine the mass of the piston.
\(\displaystyle b)\) The air inside cylinder is slowly heated. By what factor should the absolute temperature of the air be raised in order that the piston moves up 10 cm?
\(\displaystyle c)\) How much heat is added to the gas during the heating process?
(5 pont)
P. 4853. There are two concentric circular conductor loops in the same plane. The ratio of their radii is 3, and the ratio of the charges on them is \(\displaystyle -8\). At which point of the line crossing perpendicularly the plane of the loops at their centre will the electric field strength be zero?
(4 pont)
P. 4854. The figure shows the patterns of ``infinite'' connection of resistors and capacitors. The resistance of each resistor is \(\displaystyle R\), and the capacitance of each capacitor is \(\displaystyle C\). Determine the equivalent resistance and the equivalent capacitance between the points \(\displaystyle A\) and \(\displaystyle B\).
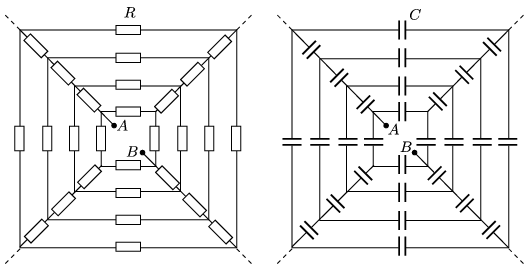
(5 pont)
P. 4855. Nitrogen-13 is a radioisotope of Nitrogen. Its half life is 10 minutes. The initial number of the nuclei of the isotope \(\displaystyle {}^{13}\rm N\) is \(\displaystyle N\).
\(\displaystyle a)\) How many nuclei decays during 20 minutes if \(\displaystyle N=10^{10}\)?
\(\displaystyle b)\) What can be stated about the number of decaying nuclei during 20 minutes if \(\displaystyle N=4\)?
(5 pont)
Upload your solutions above.
