KöMaL Problems in Physics, October 2016
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'M'Deadline expired on November 10, 2016. |
M. 362. Cut out 2 cm wide strips from different types of paper. Fix the strips in horizontal position and measure their declination as a function of the free length of the strip. Are the declinations the same when the same sheet of paper is used, but the strips are cut out from different parts of the sheet?
(6 pont)
 |
Problems with sign 'G'Deadline expired on November 10, 2016. |
G. 581. Where and how can it happen that the Sun is observed to rise in the West and not in the East?
(3 pont)
solution (in Hungarian), statistics
G. 582. The edges of an aluminium block are \(\displaystyle a=20\) cm, \(\displaystyle b=30\) cm and \(\displaystyle c=40\) cm long. The density of aluminium is \(\displaystyle \varrho=2700~\rm kg/m^3\). What is the pressure exerted by the block on the horizontal ground?
(3 pont)
solution (in Hungarian), statistics
G. 583. 2 litres of water, initially at a temperature of \(\displaystyle 20~{}^\circ\)C, was heated for ten minutes by an immersion heater, rated at 500 W. Due to this heating the temperature of the water increased to \(\displaystyle 45~{}^\circ\)C. What was the efficiency of the heating process?
(3 pont)
 |
Problems with sign 'P'Deadline expired on November 10, 2016. |
P. 4864. A body was projected at two different angles of elevation at the same initial speed, such that the range of the projection was the same in both cases. What are these two angles if the time of the motion is \(\displaystyle n\) times as much in one of the cases than in the other? Air drag is to be neglected in both cases.
(4 pont)
solution (in Hungarian), statistics
P. 4865. Two cars are undergoing uniform straight line motion along two straight motorways, which are perpendicular to each other, as shown in the figure. Initially the vehicles were at a distance of \(\displaystyle x_0=6\) km and \(\displaystyle y_0=3\) km from the cross-roads. The speed of the car moving along the path labelled \(\displaystyle AO\) is \(\displaystyle v_1=36~\)km/h. It takes 9 minutes for the cars to reach the position where they are the closest to each other during their motion.
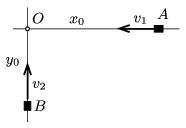
What is the speed of the car travelling along path \(\displaystyle BO\), and what is the shortest distance between them?
(5 pont)
solution (in Hungarian), statistics
P. 4866. Two pendulums of length \(\displaystyle l\) are hanging next to each other, such that the balls at their ends are touching each other as shown in the figure. The mass of one of the balls, \(\displaystyle M\), is much greater than that of the other, \(\displaystyle m\).

\(\displaystyle a)\) The pendulum on the left is displaced a bit, such that the elevation of the ball of mass \(\displaystyle M\) is \(\displaystyle h\ll \ell\), and then it is released. After the elastic collision of the balls what maximum height can the ball of mass \(\displaystyle m\) reach?
\(\displaystyle b)\) If both balls are deflected into opposite directions, such that both are raised to a height of \(\displaystyle h\ll \ell\), then what may be the maximum height to which the ball of mass \(\displaystyle m\) goes up after colliding elastically with the other ball?
(4 pont)
solution (in Hungarian), statistics
P. 4867. Two objects, which are moving into the same direction collide totally inelastically with each other. The mass of one of the objects is \(\displaystyle n\) times as much as that of the other, whilst its speed is one-\(\displaystyle n\)-th of the speed of the other (\(\displaystyle n\ge 2\) is an integer). For which \(\displaystyle n\) will at least half of the kinetic energy be dissipated?
(4 pont)
solution (in Hungarian), statistics
P. 4868. The equation of an equilibrium process of a sample of ideal gas consisting of \(\displaystyle N\) molecules is:
\(\displaystyle \frac{p}{p_0}+\frac{V}{V_0}=1. \)
What may the maximum temperature of the gas be during the process?
(4 pont)
solution (in Hungarian), statistics
P. 4869. A spring (designed for both compression and extension) of length \(\displaystyle \ell\) is compressed to a length of \(\displaystyle d<\ell/2\) with a force of \(\displaystyle F_1\). Then the spring is halved and the two alike springs are held next to each other and compressed (in parallel) again, to a length of \(\displaystyle d\). What is the magnitude of the force \(\displaystyle F_2\), which is to be exerted?
How many equal pieces should a spring of length \(\displaystyle \ell=10d\) be cut into, in order to maximize the force \(\displaystyle F_n\), which is exerted when all the pieces, held parallel, are compressed to a length of \(\displaystyle d\)? What is the magnitude of this force?
(5 pont)
solution (in Hungarian), statistics
P. 4870. At a remote place of space, there are two lead balls of equal size. The gravitational force between them is the same as the electrostatic attractive force exerted between them. The potential difference between the two balls is 5 kV. What is the size of the balls if their net charge is zero?
(4 pont)
solution (in Hungarian), statistics
P. 4871. A particle of mass \(\displaystyle m\) and of charge \(\displaystyle q\) is shot into uniform magnetic field at a speed of \(\displaystyle v\). The magnetic induction of magnitude \(\displaystyle B\), is perpendicular to the plane of the paper. Before entering into the magnetic field the particle is moving parallel to the (lower) rim of the region of magnetic field at a distance of \(\displaystyle d\) from it, as shown in the figure. When passing through the magnetic field the direction of its motion changes by an angle of \(\displaystyle \varphi=60^\circ\).

\(\displaystyle a)\) What is the sign of the charge if the induction vector points into the paper?
\(\displaystyle b)\) What is the speed of the particle?
(4 pont)
solution (in Hungarian), statistics
P. 4872. Estimate the time during which a bather in the beach of lake Balaton absorbs that amount of energy from the sunshine at noon, which would be the lethal whole-body dose in case of gamma radiation (6 Gy).
(4 pont)
solution (in Hungarian), statistics
P. 4873. A resistor of constant resistance is connected to the generator of a bicycle (sometimes wrongly named as ``dynamo''). To rotate the generator at a constant rotational speed of revolutions \(\displaystyle n\) and \(\displaystyle 2n\), the average torque to be applied is \(\displaystyle M_1\) and \(\displaystyle 1.8\,M_1\), respectively. What is the average torque in order to rotate the generator at a rotational speed of \(\displaystyle 3n\)? The mechanical losses of the generator can be neglected.
(6 pont)
Upload your solutions above.
