KöMaL Problems in Physics, November 2016
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'M'Deadline expired on December 12, 2016. |
M. 363. Fill one-fourth of a test tube with powdered chalk, and then pour water onto it such that the test tube is nearly filled. Shake well, and then let the chalk powder settle.
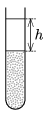
Measure how the height of the cleared water \(\displaystyle h\) depends on the time elapsed from the beginning of the settling process.
(6 pont)
 |
Problems with sign 'G'Deadline expired on December 12, 2016. |
G. 584. A father makes a see-saw for his two daughters from a 3 metre long uniform-density timber of mass 24 kg. Because the girls are not the same size the pivot is attached not to the middle of the timber, but 30 cm away from the midpoint of the timber. Sarah the smaller daughter is 10 kg now.
\(\displaystyle a)\) What is the mass of the elder sister, Emma, if the the see-saw can be balanced when the two sisters sit at the ends of it?
\(\displaystyle b)\) Sarah and Emma can use the see-saw for a long time. Plot Emma's mass as a function of Sarah's mass.
(3 pont)
solution (in Hungarian), statistics
G. 585. The density of a wooden sheet is 800 kg/m\(\displaystyle ^3\), and its width is 6 cm. To what depth below the water level will the wooden sheet sink, if it is placed into water?
What should the mass of that object be which can be put onto the wooden sheet of area 0.5 m\(\displaystyle ^2\), if the sheet is just not covered with water?
(3 pont)
solution (in Hungarian), statistics
G. 586. A ball is projected forward from an open car moving at a speed of 3 m/s. The speed of the ball is 2 m/s and it is projected at an angle of \(\displaystyle 60^\circ\) measured from the horizontal. With construction determine the angle at which the ball is flying away with respect to the road.
(3 pont)
 |
Problems with sign 'P'Deadline expired on December 12, 2016. |
P. 4874. A cyclist rides his bicycle at a constant speed of \(\displaystyle v\) along a road which is parallel to the railway. The trains, which move in the same direction as the cyclist, overtake him in \(\displaystyle t_1\) time intervals, and the trains, which move in the opposite direction as the cyclist, meet the cyclist in \(\displaystyle t_2\) time intervals. The trains depart from the two terminals in the same and equal time intervals. What is the average speed of the trains and how many minutes elapse between the departure of two (consecutive) trains?
(Data: \(\displaystyle v=14\) km/h, \(\displaystyle t_1=15\) minutes, \(\displaystyle t_2=7.5\) minutes.)
(4 pont)
solution (in Hungarian), statistics
P. 4875. A uniform-density hemisphere is placed onto a rough inclined plane of small elevation angle, and then the angle of elevation is slowly increased.
\(\displaystyle a)\) Determine the angle of elevation of the slope when the hemisphere just slips on the incline if the coefficient of static friction is 0.3. Does this angle depend on whether the hemisphere is put onto the plane with its convex or plain part?
\(\displaystyle b)\) What is the angle between the slope and the plane part of the hemisphere at the moment when the hemisphere starts to slide if it is placed on the slope with its convex part?
Hereafter suppose that the coefficient of friction between the slope and the hemisphere is much greater than the value given above. Two different types of experiments are done: the hemisphere is placed on the slope such that first the convex, then the plane part of the object touches the slope. The angle of elevation of the slope is slowly increased in both cases.
\(\displaystyle c)\) What may the maximum value of the slope angle be in each case in order that the hemisphere stays at rest? What is the least value of the coefficient of static friction in each case in order to reach the critical angle of elevation?
(5 pont)
solution (in Hungarian), statistics
P. 4876. The area of the inner cross section of the left part of a horizontal fixed tube is \(\displaystyle A\), whilst the area of the cross section of its part on the right hand-side is \(\displaystyle kA\), where \(\displaystyle k<1\) (e.g. \(\displaystyle k=\frac{1}{5})\). The two parts are attached smoothly without any sharp turns as shown in the figure. In the tube there is some liquid of density \(\displaystyle \varrho\) and of negligible viscosity. With the help of a piston at the left hand-side, the liquid can be pushed out of this part of the tube. The water which leaves the tube hits a vertical wall and spreads out, creating a tapering film of fluid.

\(\displaystyle a)\) At what constant speed does the piston move if the external force exerted on it has a constant value of \(\displaystyle F\)?
\(\displaystyle b)\) What is the force exerted by the water on the vertical wall?
\(\displaystyle c)\) What is the value of the horizontal force which is exerted by the tube on the fastening?
Suppose that the flow is constant in time (stationary), and that the effect of gravity can be neglected in the problem.
(6 pont)
solution (in Hungarian), statistics
P. 4877. A double cylinder, made of some good conducting material, can move with the help of the wheels attached to it. The wall of the cylinders have negligible width, and the areas of the inner cross section of the cylinders are \(\displaystyle A_1\) and \(\displaystyle A_2\). In the cylinders there are pistons, which are attached to walls. The distance between the pistons and the plane along which the two cylinders touch each other is \(\displaystyle L\). In the confined region there is a sample of oxygen gas at a temperature of \(\displaystyle T_0\). The ambient air pressure is \(\displaystyle p_0\).
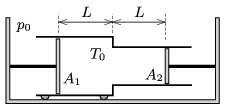
The temperature is slowly increased to \(\displaystyle T_1\).
\(\displaystyle a)\) By what amount does the double cylinder move during the temperature change?
\(\displaystyle b)\) How much heat is absorbed by the oxygen gas in the heating process?
(Data: \(\displaystyle A_1=10~\rm cm^2\), \(\displaystyle A_2=5~\rm cm^2\), \(\displaystyle L=10~\rm cm\), \(\displaystyle p_0=100\) kPa, \(\displaystyle T_0=250\) K, \(\displaystyle T_1=300\) K.)
(4 pont)
solution (in Hungarian), statistics
P. 4878. The density of the air in a volley-ball, which was inflated in the school yard, is 1.55 gram/litre. According to the calculations the root-mean-square speed of the oxygen molecules is 477 m/s.
\(\displaystyle a)\) What is the root-mean-square speed of the nitrogen molecules in the ball?
\(\displaystyle b)\) What is the pressure of the air inside the ball? Is the ball pumped to the appropriate pressure?
(4 pont)
solution (in Hungarian), statistics
P. 4879. According to a science-fiction film four spaceships are moving together somewhere in the remote space without using their engines. The spaceships are at the four vertices of a regular tetrahedron of edges 10 km. The mass of each spaceship is \(\displaystyle 2\cdot 10^8\) kg. (The size of the spaceships is much smaller than the distance between them.)
\(\displaystyle a)\) What is the magnitude and the direction of the gravitational force exerted on the spaceships?
\(\displaystyle b)\) What is the charge on each spaceship, if the distance between them remains constant in time?
\(\displaystyle c)\) How would the four spaceships move if each used its engine for a short time and each started to move towards the centre of the tetrahedron at a speed of \(\displaystyle v_0=10\) m/s?
(4 pont)
solution (in Hungarian), statistics
P. 4880. At the centre of a solenoid of diameter \(\displaystyle d=4.4\) cm, of length \(\displaystyle \ell=1\) m and of \(\displaystyle N=1000\) number of turns, there is a thick, circular, conducting coaxial ring. The ring has a radius of \(\displaystyle r=2.5\) cm, and its resistance is \(\displaystyle R=10^{-4}~\Omega\). The \(\displaystyle 50\) A current in the solenoid is changed to \(\displaystyle -50\) A in 1 second.
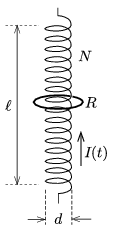
\(\displaystyle a)\) What is the magnitude of the magnetic induction at the centre of the ring when the current in the solenoid is zero?
\(\displaystyle b)\) What is this value \(\displaystyle \Delta t=0.001\) s before and after the above described moment?
(5 pont)
solution (in Hungarian), statistics
P. 4881. \(\displaystyle N\) converging lenses of focal length \(\displaystyle 2f\) and \(\displaystyle N\) diverging lenses of focal length \(\displaystyle -f\) are placed in turns onto an optical bench at a distance of \(\displaystyle f\) from each other. Then parallel to their common principal axis a beam of light of diameter \(\displaystyle D\) passes through the system of lenses
\(\displaystyle a)\) from the left;
\(\displaystyle b)\) from the right.
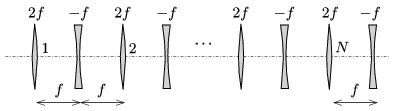
What is the light beam emerging from the system of lenses like?
(4 pont)
solution (in Hungarian), statistics
P. 4882. In a nuclear reactor the energy of the emerging fast neutrons during the fission of uranium is in the order of MeV. In order to use these neutrons to split more atoms they have to be slowed down to the level of the so called ``thermal energy'' when their speed is just about 2.2 km/s.
The slowing process of neutrons can be done with the nuclides of light elements (for example the deuterium in heavy water can be used) such that the nuclides of the light element (deuterons) collide totally elastically with the neutrons.
\(\displaystyle a)\) Approximately after how many collisions will a fast neutron slow down to the thermal energy? (It can be assumed that the initial kinetic energy of the deuterons before the collisions is negligible, and the collisions are head-on.)
\(\displaystyle b)\) What is the order of the kinetic energy of the thermal neutrons and what is their ``temperature''?
(4 pont)
solution (in Hungarian), statistics
P. 4883. Some electrons are moving in the magnetic field of 0.03 T of a particle accelerator along a circular path of radius 0.2 m. What is the speed of the electrons?
(5 pont)
Upload your solutions above.
