KöMaL Problems in Mathematics, March 2017
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on April 10, 2017. |
K. 541. Anna's income is \(\displaystyle \frac{5}{8}\) of Betty's income, while Anna's monthly expenses are only one half of what Betty spends a month. Anna puts 40% of all her income aside each month. What percentage of her monthly income does Betty put aside?
(6 pont)
solution (in Hungarian), statistics
K. 542. A shop sells a certain souvenir for 1100 forints (HUF, Hungarian currency). A tourist from an exotic country wants to buy one by paying for it with the currency of his own country. In his country, there are three kinds of coins: round, triangular and square. 11 round coins are worth exactly 1500 forints, 11 square coins are worth 1600 forints, and 11 triangular coins are worth 1700 forints. How many of each type of coin should the tourist hand over in order to pay the exact price of 1100 forints? Find all possible answers.
(6 pont)
solution (in Hungarian), statistics
K. 543. In a food store, 27 cubical boxes are arranged to form a large cube. In each box, there is a large piece of cheese. A mouse crawls into one of the boxes lying on the floor and eats the cheese he finds there. Then he moves to another nonempty box that has a face in common with the first box, and eats the cheese again. He continues in this way. Is it possible for the mouse to organize his moves so that he should finish
\(\displaystyle a)\) in the box at the centre of a face of the large cube?
\(\displaystyle b)\) in the box in the interior of the large cube?
(6 pont)
solution (in Hungarian), statistics
K. 544. Triangular numbers are defined as the numbers that can be represented as the sum of the first few consecutive natural numbers (\(\displaystyle 1, 3, 6, 10, \ldots\)). Hexagonal numbers are defined by the (infinite) sequence of diagrams represented below. Find all hexagonal numbers that are also triangular numbers.
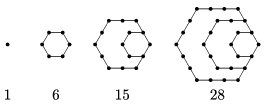
(6 pont)
solution (in Hungarian), statistics
K. 545. The three solids shown in the diagrams below are made up of small cubes. If the construction is continued in the same way, how many small cubes will the tenth solid consist of?
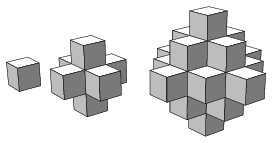
(6 pont)
solution (in Hungarian), statistics
K. 546. Barbara chooses two numbers out of the set \(\displaystyle A = \{8, 9, 10\}\) at random, and adds them together. Matthew chooses two numbers out of the set \(\displaystyle M = \{3, 5, 6\}\) at random and multiplies them together. What is the probability that Barbara's result is larger?
(6 pont)
 |
Problems with sign 'C'Deadline expired on April 10, 2017. |
C. 1406. What is the four-digit number \(\displaystyle \overline{abcd}\) if \(\displaystyle a+b=c+d\), \(\displaystyle a+d=c\), \(\displaystyle {2(a+c)}=b+d\), and \(\displaystyle 3\overline{ab}=\overline{cd}\)?
(5 pont)
solution (in Hungarian), statistics
C. 1407. In a parallelogram \(\displaystyle ABCD\), \(\displaystyle M\) and \(\displaystyle N\) are points on sides \(\displaystyle AD\) and \(\displaystyle DC\), respectively, such that \(\displaystyle \frac{AM}{MD}=\frac{DN}{NC}=\frac{7}{11}\). Let \(\displaystyle P\) denote the intersection of lines \(\displaystyle BM\) and \(\displaystyle AN\).
Prove that the areas of triangle \(\displaystyle APB\) and quadrilateral \(\displaystyle DMPN\) are equal.
(Based on the idea of L. Longáver, Nagybánya)
(5 pont)
solution (in Hungarian), statistics
C. 1408. Eight different dominoes are laid on the table, according to the rules of the game, so that they form a closed-up square (the figure shows a possible arrangement). What are the smallest and largest possible values of the sum of the dots on the dominoes?
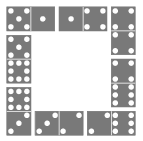
(5 pont)
solution (in Hungarian), statistics
C. 1409. The trunk of an old plane tree is cylindrical, with a perimeter of 2 metres. On one side of the tree trunk, a snail is crawling up the tree, in the plane of the axis of the cylinder. There are only 3 cm remaining from a height of 2 metres. In that time instant, another snail is just about to start its journey up the tree on the opposite side when they both notice each other. The two snails immediately start to crawl towards each other along the shortest possible path. What distance will they cover until they meet if their speeds are equal?
(5 pont)
solution (in Hungarian), statistics
C. 1410. Let \(\displaystyle b=\sqrt{a+\sqrt a}\,\), where \(\displaystyle a\) is a positive integer. Prove that \(\displaystyle b\) cannot be an integer.
(5 pont)
solution (in Hungarian), statistics
C. 1411. The angle at vertex \(\displaystyle C\) of a triangle \(\displaystyle ABC\) is \(\displaystyle 120^{\circ}\). \(\displaystyle D\) is the point of side \(\displaystyle AB\) such that \(\displaystyle CD\) is an angle bisector. Show that
\(\displaystyle \frac{1}{CD}=\frac{1}{AC}+\frac{1}{BC}. \)
(D. Fülöp, Pécs)
(5 pont)
solution (in Hungarian), statistics
C. 1412. For what natural numbers \(\displaystyle n\) is there a simple planar graph of \(\displaystyle n\) points and \(\displaystyle 2n\) edges in which the faces cannot be coloured in two colours so that faces with an edge in common should have different colours?
(5 pont)
 |
Problems with sign 'B'Deadline expired on April 10, 2017. |
B. 4858. Points \(\displaystyle A\) and \(\displaystyle B\) are separated by a unit distance. The unit circles \(\displaystyle k_A\) and \(\displaystyle k_B\) centred at \(\displaystyle A\) and \(\displaystyle B\) intersect at points \(\displaystyle C\) and \(\displaystyle D\), respectively. Let \(\displaystyle k_C\) denote the circle centred at \(\displaystyle C\) and passing through \(\displaystyle D\). \(\displaystyle F\) is that intersection of line \(\displaystyle AC\) and circle \(\displaystyle k_C\) which is farther away from \(\displaystyle A\). \(\displaystyle G\) is the other intersection of circle \(\displaystyle k_A\) and line \(\displaystyle DF\). Show that \(\displaystyle \angle GAD=90^\circ\).
(3 pont)
solution (in Hungarian), statistics
B. 4859. Rudi chose a positive integer \(\displaystyle k\), and observed that \(\displaystyle 4^k\) and \(\displaystyle 5^k\) began with the same digit in decimal notation. Prove that this digit may only be a \(\displaystyle 2\) or a \(\displaystyle 4\).
(German problem)
(4 pont)
solution (in Hungarian), statistics
B. 4860. Assume that \(\displaystyle a<b<c<d\) and \(\displaystyle a+d\ne b+c\). Show that the equation
\(\displaystyle \frac1{a-x}-\frac1{b-x}-\frac{1}{c-x}+\frac1{d-x}=0 \)
has exactly two distinct roots, such that one of them lies in the interval \(\displaystyle (b,c)\), and the other one lies outside the interval \(\displaystyle (a,d)\).
(3 pont)
solution (in Hungarian), statistics
B. 4861. Let \(\displaystyle r\) and \(\displaystyle R\), respectively, denote the radii of the inscribed and circumscribed circles of a right-angled triangle \(\displaystyle ABC\). Let \(\displaystyle CD\) be the altitude drawn to the hypotenuse \(\displaystyle AB\). Draw the square \(\displaystyle CEFG\) of side length \(\displaystyle CD\) that has vertex \(\displaystyle E\) on side \(\displaystyle AC\) and vertex \(\displaystyle G\) on side \(\displaystyle BC\). Let \(\displaystyle T\) and \(\displaystyle t\), respectively, denote the parts of the area of the square \(\displaystyle CEFG\) which lie inside and outside the triangle \(\displaystyle ABC\). Prove that
\(\displaystyle \frac{t}{T}=\frac{r}{2R}. \)
(B. Bíró, Eger)
(4 pont)
solution (in Hungarian), statistics
B. 4862. \(\displaystyle M\), \(\displaystyle N\), \(\displaystyle P\), \(\displaystyle Q\), and \(\displaystyle R\), respectively, are the midpoints of the sides \(\displaystyle AB\), \(\displaystyle BC\), \(\displaystyle CD\), \(\displaystyle DE\) and \(\displaystyle EA\) of a convex pentagon \(\displaystyle ABCDE\). Show that if the line segments \(\displaystyle AP\), \(\displaystyle BQ\), \(\displaystyle CR\) and \(\displaystyle DM\) are concurrent then the common point also lies on line segment \(\displaystyle EN\).
(S. Róka, Nyíregyháza)
(5 pont)
solution (in Hungarian), statistics
B. 4863. In a triangle \(\displaystyle ABC\), \(\displaystyle AB=BC\). \(\displaystyle D\) is an interior point of the triangle such that \(\displaystyle \angle ADC= 2 \angle ABC\). Prove that the distance of point \(\displaystyle B\) from the exterior angle bisector of \(\displaystyle \angle ADC\) is the arithmetic mean of the line segments \(\displaystyle AD\) and \(\displaystyle DC\).
(Kvant)
(5 pont)
solution (in Hungarian), statistics
B. 4864. A sack contains 100 red balls and 100 blue balls. Balls are drawn at random one by one, without replacement, until all 100 red balls are drawn out. Determine the expected value of the number of balls remaining in the sack.
(5 pont)
solution (in Hungarian), statistics
B. 4865. In an acute-angled triangle, \(\displaystyle f\) and \(\displaystyle g\) are the line segments that divide the angle enclosed by sides \(\displaystyle a\) and \(\displaystyle b\) into three equal parts. Prove that
\(\displaystyle \frac{f+g}{2}< \frac{2}{\frac{1}{a} +\frac{1}{b}}. \)
(6 pont)
solution (in Hungarian), statistics
B. 4866. Xavier and Yvette take turns in choosing
\(\displaystyle a)\) real numbers;
\(\displaystyle b)\) complex numbers.
Xavier starts, and the game ends after the 100th number. Let the numbers be \(\displaystyle a_1,\dots,a_{100}\). Yvette's goal is to make the sum \(\displaystyle a_1a_2+a_1a_3+\ldots +a_{99}a_{100}\) of the products of the \(\displaystyle \lbinom{100}2\) pairs of the numbers equal to 0, while Xavier is trying to avoid that. Who has got a winning strategy?
(6 pont)
 |
Problems with sign 'A'Deadline expired on April 10, 2017. |
A. 692. Do there exist bijective functions \(\displaystyle f,g\colon \mathbb{Q}\to\mathbb{Q}\) such that the function \(\displaystyle f\big(g(x)\big)\) is strictly increasing, but the function \(\displaystyle g\big(f(x)\big)\) is strictly decreasing?
(5 pont)
solution (in Hungarian), statistics
A. 693. Let \(\displaystyle A\) and \(\displaystyle B\) be two vertices of a convex polygon \(\displaystyle \mathcal{P}\) with maximum distance from each other. Let the perpendicular bisector of the segment \(\displaystyle AB\) meet the boundary of \(\displaystyle \mathcal{P}\) at points \(\displaystyle C\) and \(\displaystyle D\). Show that the perimeter of \(\displaystyle \mathcal{P}\) is less than \(\displaystyle 2(AB+CD)\).
(5 pont)
A. 694. Prove that the inequality
\(\displaystyle \frac1{\sqrt{2x}} + \frac1{\sqrt{2y}} + \frac2{\sqrt{x+y}} + 2 \ge \frac4{\sqrt{x+2}} + \frac4{\sqrt{y+2}} \)
holds for all pairs \(\displaystyle (x,y)\) of positive real numbers.
(5 pont)
Upload your solutions above.
