KöMaL Problems in Physics, September 2017
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'M'Deadline expired on October 10, 2017. |
M. 370. Measure the tilt angle of at least three different types of grainy food .(e.g. rice, poppy seed, flour, granulated sugar or powdered sugar).
(6 pont)
 |
Problems with sign 'G'Deadline expired on October 10, 2017. |
G. 605. Two trains are travelling along two parallel tracks. The speed of one of them is 80 km/h. The distance between them is 4.8 km, and after a quarter of an hour the distance between them is the same. What is the speed of the other train if both trains have the same length of 200 m?
(3 pont)
solution (in Hungarian), statistics
G. 606. The heat capacity of a calorimeter is to be measured, therefore 65 g water at a temperature of \(\displaystyle 45~{}^\circ\)C is poured into the calorimeter, which has already contained for a long time 150 g water at a temperature of \(\displaystyle 17~{}^\circ\)C. The final temperature of the mixture is \(\displaystyle 25~{}^\circ\)C. What is the heat capacity of the calorimeter?
(3 pont)
solution (in Hungarian), statistics
G. 607. Calculate the equivalent resistance of the circuit shown in the figure across points \(\displaystyle A\) and \(\displaystyle B\), and across the points \(\displaystyle C\) and \(\displaystyle D\).
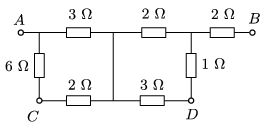
(3 pont)
solution (in Hungarian), statistics
G. 608. The magnetic effect of a relatively weak electric current flowing in a piece of vertical wire is to be shown by means of a compass. Before the current is switched on where should the compass be placed in order that due to the current the pointer deviates the most from the north-south direction?
(3 pont)
 |
Problems with sign 'P'Deadline expired on October 10, 2017. |
P. 4949. A man is exercising on a stationary bike, which has a magnetic resistance mechanism. What is the work performed by the muscles of the man's legs transferred to?
(3 pont)
solution (in Hungarian), statistics
P. 4950. A car of mass 1200 kg started from rest and speeded up at an acceleration of 2 m/s\(\displaystyle {}^2\) along a straight horizontal path of length 200 m. Its wheels did not slide.
\(\displaystyle a)\) What was the total frictional force exerted between the ground and the wheels?
\(\displaystyle b)\) What is the final kinetic energy of the car? (The mass of the wheels can be neglected.)
\(\displaystyle c)\) How much work was done by the static frictional force?
(4 pont)
solution (in Hungarian), statistics
P. 4951. Approximately by what distance does the Earth's path diverges from the straight line in one second, during its revolution around the Sun?
(4 pont)
solution (in Hungarian), statistics
P. 4952. On a Physics lesson the teacher wants to check experimentally the result of the following, previously calculated problem (see the solution of exercise G. 587. on page 371:)
"A 2 N force is exerted on an initially stationary, easily moveable trolley of mass \(\displaystyle m=1.6\) kg for 0.5 s, and after the force ceased the trolley moves freely along the horizontal path. What distance is covered by the trolley during the first second after it started moving?"
How should the mass \(\displaystyle M\) of the weight shown in the figure be chosen, and what should the distance \(\displaystyle h\) be? (The masses of the wheels of the trolley, the pulley and the thread are negligible.)
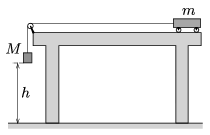
(4 pont)
solution (in Hungarian), statistics
P. 4953. Some argon gas is put into a Torricelli-tube of length \(\displaystyle L=1\) m and of cross section \(\displaystyle A=2\) cm\(\displaystyle {}^2\), therefore the height of the mercury in the tube is only \(\displaystyle h_1=0.4\) m. The ambient air pressure is \(\displaystyle p_0=10^5\) Pa, and the initial temperature is 20 \(\displaystyle {}^\circ\)C.
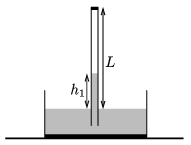
\(\displaystyle a)\) What is the mass of the argon gas above the mercury?
\(\displaystyle b)\) The temperature of the gas is slowly increased. What is the temperature of the gas when the height of the mercury in the tube is \(\displaystyle h_2=0.36\) m?
\(\displaystyle c)\) How much work was done by the extending gas during the process?
(5 pont)
solution (in Hungarian), statistics
P. 4954. One end of a metre stick, which has fairly big mass, can be rotated freely about a horizontal axle. Put 11 five-forint coins onto the initially horizontal stick at a distance of 10 cm from each other.
\(\displaystyle a)\) What happens to the coins right after the moment when the stick was released?
\(\displaystyle b)\) Which coins do not move with respect to the stick at the moment when the stick encloses an angle of 10\(\displaystyle {}^\circ\) with its original position? The coefficient of static friction between the stick and the coins is 0.5.
(5 pont)
solution (in Hungarian), statistics
P. 4955. Two small balls of mass \(\displaystyle m\) and of charge \(\displaystyle Q\) are moving on the horizontal ground, and at a certain instant they are at a distance of \(\displaystyle d\). At this instant their speeds are \(\displaystyle v_0\), and the direction of their velocity vectors makes an angle of \(\displaystyle \alpha\) with the direction of the line connecting the two balls, as shown in the figure.
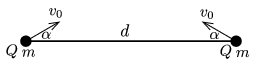
\(\displaystyle a)\) What is the least distance between the balls?
\(\displaystyle b)\) What are their speeds at this moment?
(5 pont)
solution (in Hungarian), statistics
P. 4956. At a certain instant the symmetry axis of the parabolic mirror of an astronomical telescope is vertical. The focal length of the mirror is \(\displaystyle f\). At this instant the rim of the mirror is at a height of \(\displaystyle H\) with respect to the lowest point of the mirror. A small object of mass \(\displaystyle m\), starting from the rim of the mirror slides down on the mirror frictionlessly to the centre of the mirror. What is the force exerted by the small object at the centre of the mirror?
(5 pont)
solution (in Hungarian), statistics
P. 4957. The sides of a square-shaped frame, shown in the figure are made of wires of resistances \(\displaystyle r_1\) and \(\displaystyle r_2\). The frame is in uniform magnetic field, which is perpendicular to the plane of the figure and is increasing at a constant rate. What should the resistance \(\displaystyle R\) of the wire connected across the diagonal of the frame be, in order that this wire is warmed up at the greatest rate?
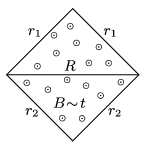
(5 pont)
solution (in Hungarian), statistics
P. 4958. In a piece of uranium ore there are 200 million \(\displaystyle {}^{233}\)U atoms. The half-life of the \(\displaystyle {}^{233}\)U isotope is \(\displaystyle 1.6\cdot10^5\) years, and it decays to \(\displaystyle {}^{229}\)Th, the half-life of which is \(\displaystyle 7.{}8\cdot10^3\) years. This decays to \(\displaystyle {}^{225}\)Ra, which has a half-life of 15 days. Estimate the number of \(\displaystyle {}^{225}\)Ra nuclei in the uranium ore.
(5 pont)
solution (in Hungarian), statistics
P. 4959. One of the vertices of a regular pentagon-shaped thin metal sheet is earthed, whilst to the others voltage supplies of small internal resistance are connected, as shown in the figure. What is the reading on the voltmeter connected to the centre of the sheet?
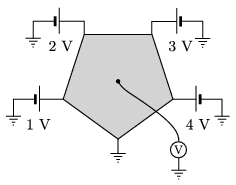
(6 pont)
Upload your solutions above.
