KöMaL Problems in Mathematics, September 2017
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on October 10, 2017. |
K. 547. Peter thought of a positive integer. He added the number containing the same digits in reverse order. (For example, starting with 26 he added 62 to it, or starting with 530 he added 35.) He obtained a three-digit number that only contained digits of 6 and/or 9. What may have been Peter's original number?
(6 pont)
solution (in Hungarian), statistics
K. 548. We have four boxes numbered 1 to 4, and four cards with the numbers 1, 2, 3, 4 on them. We place one card in each box, according to the following rule: every card shows the number of the box that contains the card corresponding to the number of the box containing it. In how many different ways is it possible to place the cards in the boxes?
(6 pont)
solution (in Hungarian), statistics
K. 549. Three cars are travelling along the same road, in the same direction but at different uniform speeds. In principle, there are six possible orders for the three cars behind each other. Is it possible that all six orders actually occur during their journey?
(Proposed by L. Loránt, Budapest)
(6 pont)
solution (in Hungarian), statistics
K. 550. An unusual telegraph company charges for the various words by the letters they contain. Consonants are free, but each vowel costs a certain amount. We do not know these prices, but we do know the charges for a few words we have sent before: TÉGLALAP, PARALELOGRAMMA, NÉGYZET, HÁROMSZÖG, NÉGYSZÖG, ROMBUSZ, TRAPÉZ, DELTOID. (These are all mathematical terms in Hungarian. Y is not a vowel, and vowels with accents on them count as different vowels.) Show a possible method to determine the charge for the word GEOMETRIA.
(6 pont)
solution (in Hungarian), statistics
K. 551. Find appropriate positive integers \(\displaystyle x > y > z\) such that
\(\displaystyle \frac{1}{x^{2}} + \frac{1}{y^{2}} = \frac{1}{z^{2}} \)
should hold.
(6 pont)
solution (in Hungarian), statistics
K. 552. What is the largest divisor of 9900 that is divisible by 22, 33 and 55, but not divisible by 44, 50 or 99?
(6 pont)
 |
Problems with sign 'C'Deadline expired on October 10, 2017. |
C. 1427. Divide a square into ten acute-angled isosceles triangles.
(Elemente der Mathematik)
(5 pont)
solution (in Hungarian), statistics
C. 1428. The product of four consecutive odd numbers ends in a digit of 9. What may be the preceding digit?
(Matlap, Kolozsvár [Cluj-Napoca])
(5 pont)
solution (in Hungarian), statistics
C. 1429. Ten points are placed in a \(\displaystyle 5\mathrm{~cm}\times8\mathrm{~cm}\) rectangle. Prove that there are two points separated by a distance of at most \(\displaystyle \sqrt{10}\) cm.
(5 pont)
solution (in Hungarian), statistics
C. 1430. Determine all natural numbers \(\displaystyle x\) and \(\displaystyle y\) such that \(\displaystyle \frac{20}{x}+\frac{17}{y}=1\), and \(\displaystyle xy\) is a perfect square.
(Proposed by B. Kovács, Szatmárnémeti)
(5 pont)
solution (in Hungarian), statistics
C. 1431. The lengths of the shorter base of a trapezium, then one leg, then the other leg and finally the longer base, in this order, form an arithmetic progression. Given that the length of the shortest side is 3 cm, and one of the angles lying on the longer base is 60 degrees, what is the common difference of the arithmetic progression?
(5 pont)
solution (in Hungarian), statistics
C. 1432. Let \(\displaystyle n\) be a positive integer. Show that there exists an \(\displaystyle n\)-digit number that is divisible by \(\displaystyle 2^n\), and only contains digits of 1 and 2.
(5 pont)
solution (in Hungarian), statistics
C. 1433. Four \(\displaystyle r\times6r\) rectangles are assembled to form a flexible rhombus, hinged on circles of radius \(\displaystyle r\) at the vertices. The circles touch the shorter sides of the rectangles at the midpoints (see the figure). The circles can be moved to change the angles of the rhombus, but the rectangles may not overlap. What are the smallest and the largest possible angles?
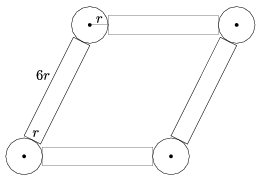
(5 pont)
 |
Problems with sign 'B'Deadline expired on October 10, 2017. |
B. 4885. Let \(\displaystyle k\) and \(\displaystyle m\) be two distinct 14-digit positive integers, each containing two of each digit 1, 2, 3, 4, 5, 6 and 7 (like 22133456456717, for example). Prove that \(\displaystyle \frac km\) cannot be an integer.
(M&IQ)
(4 pont)
solution (in Hungarian), statistics
B. 4886. How many different convex polyhedra are determined by the vertices of a cube? (Two polyhedra are considered different if they are not congruent.)
(3 pont)
solution (in Hungarian), statistics
B. 4887. Prove that there are infinitely many number pairs \(\displaystyle (a,b)\), such that \(\displaystyle a+\frac{1}{b}=b+\frac{1}{a}\), where \(\displaystyle a\ne b\). Find the possible values of \(\displaystyle ab\).
(Proposed by J. Szoldatics, Budapest)
(3 pont)
solution (in Hungarian), statistics
B. 4888. From his third birthday onwards, Sebastian always gets a birthday cake shaped like a triangular prism, with one candle in each of the three upper vertices, and as many further candles on the top as needed to make the total equal to his age. No three candles are collinear. Sebastian wants to cut the cake into triangular pieces with vertices at the positions of the candles, without other candles in the interior of the triangles. How many pieces can he form on his \(\displaystyle k\)th birthday?
(4 pont)
solution (in Hungarian), statistics
B. 4889. The trapezium \(\displaystyle ABCD\) has an inscribed circle. The circle touches base \(\displaystyle AB\) at point \(\displaystyle T\), and the parallel base \(\displaystyle CD\) at point \(\displaystyle U\). Let \(\displaystyle M\) denote the intersection of the lines of legs \(\displaystyle AD\) and \(\displaystyle BC\), and let \(\displaystyle V\) be the intersection of side \(\displaystyle AB\) with line \(\displaystyle MU\). Show that \(\displaystyle AT=VB\).
(4 pont)
solution (in Hungarian), statistics
B. 4890. Solve the following equation on the set of positive integers:
\(\displaystyle x-y-\frac xy-\frac{x^3}{y^3}+\frac{x^4}{y^4} = 2017. \)
(Proposed by B. Kovács, Szatmárnémeti)
(5 pont)
solution (in Hungarian), statistics
B. 4891. The circles \(\displaystyle S_1\), \(\displaystyle S_2\), \(\displaystyle S_3\) pairwise touch each other on the outside. Let \(\displaystyle A\), \(\displaystyle B\) and \(\displaystyle C\) denote the common points of the circles \(\displaystyle S_1\) and \(\displaystyle S_2\), \(\displaystyle S_1\) and \(\displaystyle S_3\), \(\displaystyle S_2\) and \(\displaystyle S_3\), respectively. Line \(\displaystyle AB\) intersects the circles \(\displaystyle S_2\) and \(\displaystyle S_3\) again at points \(\displaystyle D\) and \(\displaystyle E\), respectively. Line \(\displaystyle DC\) intersects circle \(\displaystyle S_3\) again at \(\displaystyle F\). Prove that triangle \(\displaystyle DEF\) is right-angled.
(Kvant)
(5 pont)
solution (in Hungarian), statistics
B. 4892. Two players, First and Second, play the following game: they place 2017 pebbles on the table. First starts by removing 1 pebble. Then Second may choose to remove either 1 or 2. Then First may remove 1, 2, 3 or 4. Then Second may remove any number from 1 to 8. And so on, the player in the \(\displaystyle i\)th step needs to remove at least 1 and at most \(\displaystyle 2^{i-1}\) pebbles. The player removing the last pebble from the table wins the game. Who has a winning strategy?
(6 pont)
solution (in Hungarian), statistics
B. 4893. In a triangle \(\displaystyle ABC\), \(\displaystyle AB\ne BC\). The angle bisector drawn from point \(\displaystyle B\) intersects side \(\displaystyle AC\) at point \(\displaystyle D\), and intersects the circumscribed circle again at point \(\displaystyle E\). The circle of diameter \(\displaystyle DE\) intersects the circumscribed circle again at a point \(\displaystyle F\), different from \(\displaystyle E\). Prove that the reflection of line \(\displaystyle BF\) about the line \(\displaystyle BD\) results in a median of triangle \(\displaystyle ABC\).
(6 pont)
 |
Problems with sign 'A'Deadline expired on October 10, 2017. |
A. 701. An airline operates flights between any two capital cities in the European Union. Each flight has a fixed price which is the same in both directions. Furthermore, the flight prices from any given city are pairwise distinct. Anna and Bella wish to visit each city exactly once, not necessarily starting from the same city. While Anna always takes the cheapest flight from her current city to some city she hasn't visited yet, Bella always continues her tour with the most expensive flight available. Is it true that Bella's tour will surely cost at least as much as Anna's tour?
(Based on a Soviet problem)
(5 pont)
solution (in Hungarian), statistics
A. 702. Fix a triangle \(\displaystyle ABC\). We say that triangle \(\displaystyle XYZ\) is elegant if \(\displaystyle X\) lies on segment \(\displaystyle BC\), \(\displaystyle Y\) lies on segment \(\displaystyle CA\), \(\displaystyle Z\) lies on segment \(\displaystyle AB\), and \(\displaystyle XYZ\) is similar to \(\displaystyle ABC\) (i.e., \(\displaystyle \angle A=\angle X\), \(\displaystyle \angle B=\angle Y\), \(\displaystyle \angle C=\angle Z\)). Of all the elegant triangles, which one has the smallest perimeter?
(5 pont)
A. 703. Let \(\displaystyle n\ge 2\) be an integer. We call an ordered \(\displaystyle n\)-tuple of integers primitive if the greatest common divisor of its components is \(\displaystyle 1\). Prove that for every finite set \(\displaystyle H\) of primitive \(\displaystyle n\)-tuples, there exists a non-constant homogenous polynomial \(\displaystyle f(x_1,x_2,\dots,x_n)\) with integer coefficients whose value is \(\displaystyle 1\) at every \(\displaystyle n\)-tuple in \(\displaystyle H\).
(Based on the sixth problem of the 58th IMO, Brazil)
(5 pont)
Upload your solutions above.
