KöMaL Problems in Physics, October 2017
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'M'Deadline expired on November 10, 2017. |
M. 371. Suspend two alike AA battery bifilarly and make them collide, such that they move along their longer symmetry axis, and collide with their negative terminals, which is on their flatter sides. Determine the coefficient of restitution (which is the ratio of the relative velocity after collision to that of before collision). Carry out the measurement with two new batteries, with a new one and a discharged one, and with two discharged ones.
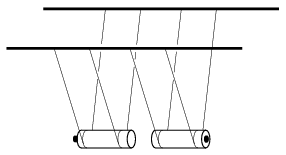
(6 pont)
 |
Problems with sign 'G'Deadline expired on November 10, 2017. |
G. 609. A man leans against the wall of a house in a peculiar way as shown in the figure, and exerts a force of \(\displaystyle F\) onto the wall. If he is observed from the reference frame of the ground, the man does not perform work, because his displacement is zero. According to another observer who is travelling in a car, moving at a speed of \(\displaystyle v\), the man exerts a constant force while moving a long distance, so he does work. Why doesn't the man leaning against the house get exhausted?
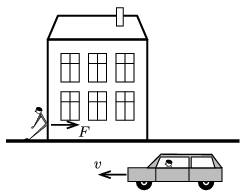
(3 pont)
solution (in Hungarian), statistics
G. 610. A meteorite of mass \(\displaystyle m\), of specific heat capacity \(\displaystyle c\) and of specific latent heat of fusion \(\displaystyle L\), consists of some material which is extremely good heat conductor. When it reaches the atmosphere of the Earth the temperature of the meteorite is \(\displaystyle \Delta T\) below its melting point. In the atmosphere due to friction heat is generated in it at a rate of \(\displaystyle P\). How long does it take for the meteorite to be melted totally?
(3 pont)
solution (in Hungarian), statistics
G. 611. What is the area of a floating ice floe of thickness 30 cm if it can hold an 80 kg man?
(3 pont)
solution (in Hungarian), statistics
G. 612. From the window of a house close to the M3 motorway stretch, starting at Budapest, we observe a Boeing 737 – ready to land at Ferihegy – flying above us. A crow permanently follows the plane (seemingly the ``bird flies next to the plane''), and the wingspan of the crow seems to have the same length as the length of one of the wings of the plane. Estimate at what height and at what speed the crow flies. (Look up the missing data.)
(3 pont)
 |
Problems with sign 'P'Deadline expired on November 10, 2017. |
P. 4960. A uniform density rod of mass 1 kg is suspended horizontally at its trisecting points with two vertical threads. Two light bags are attached to the ends of the rod (one to each end) then first only one of them and then the other one as well were filled with biscuits. The rod must stay in its horizontal position all the time, such that it cannot be touched. Altogether how much biscuit can be put into the two bags?
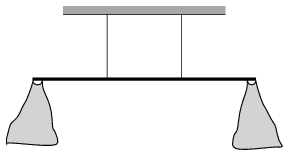
(4 pont)
solution (in Hungarian), statistics
P. 4961. An object executes simple harmonic motion of period \(\displaystyle T=0.2\) s. It takes \(\displaystyle \Delta t=0.01\) s to double its displacement of \(\displaystyle x=3\) cm. What is the amplitude of the motion?
(4 pont)
solution (in Hungarian), statistics
P. 4962. There are two cylinder-shaped wooden billets, each having a mass of mass 45 kg, in a vertical wall sewage, which contains water in it. The two billets have the same size and the same material; they touch each other and the walls of the sewage. One of them is totally under the water, whilst only half of the other one is immersed into the water. Friction is negligible everywhere.
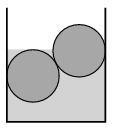
\(\displaystyle a)\) What is the density of the wood?
\(\displaystyle b)\) What are the forces exerted by the billets on the vertical walls?
(4 pont)
solution (in Hungarian), statistics
P. 4963. There is a socket at a height of \(\displaystyle H\) above a horizontal tabletop. The charger of our mobile phone has a flexible wire of length \(\displaystyle h\) and the length of the small, light and rigid part which is joined to the phone is \(\displaystyle s\). The phone which is attached to the charger is put onto the table such that it touches the table with one of its shorter side, but from some positions – when the distance \(\displaystyle d\) is greater than the value shown in the to scale figure – the phone slips. The length of the phone is \(\displaystyle \ell\), its width is negligible, and it has uniform density.
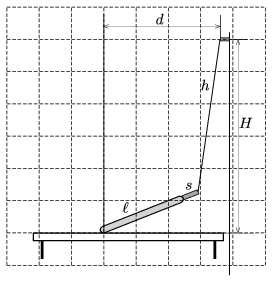
Determine with construction the numerical value of the coefficient of static friction between the tabletop and the phone.
(4 pont)
solution (in Hungarian), statistics
P. 4964. What is the least force with which an ice cube sliding on ice can be turned over? (Friction is negligible.)
(5 pont)
solution (in Hungarian), statistics
P. 4965. Just half of a flexible pearl necklace, which can slip easily, is lying on a horizontal tabletop, whilst its other half is hanging down vertically, at the edge of the table. If the necklace is released without initial speed, then it slides down from the tabletop – moving faster and faster. At some certain position of the necklace, next to the edge of the table the beads do not turn abruptly, but move over the edge, and the hanging part of the necklace begins to wave as a whip. What fraction of the necklace is on the table when this wavy motion begins?
(5 pont)
solution (in Hungarian), statistics
P. 4966. It is easy to show that the height of a mirror in which a man of height \(\displaystyle H\) can see himself from top to bottom is at least \(\displaystyle H/2\). Of course the mirror must be placed to the appropriate height on the wall. But what happens when the mirror is not vertical?
What is the least size of the mirror, when the angle between the plane of the mirror and the wall is \(\displaystyle \alpha\), and the eyes of the observer of height \(\displaystyle H\) is at a distance of \(\displaystyle d\) from the mirror?
(5 pont)
solution (in Hungarian), statistics
P. 4967. Initially the plates of a big parallel plate condenser are vertical. The top end of the thread, of length \(\displaystyle \ell=10\) cm, of a simple pendulum is fixed at a point which is equidistant from the two plates. Both the condenser and the small-mass pendulum bob are charged. The angle between the thread and the vertical is \(\displaystyle \alpha=30^\circ\).
\(\displaystyle a)\) At what angle and into which direction should the plates of the condenser be tilted in order that the thread gets parallel to the plates of the condenser?
\(\displaystyle b)\) At this position of the condenser what is the least initial speed at which the bob should be pushed perpendicularly to the thread in order that the bob moves along the circular path to which it is restricted by the thread?
(5 pont)
solution (in Hungarian), statistics
P. 4968. The heating elements of an electric heater can be connected as shown in the figure. When voltage is applied across points \(\displaystyle A\) and \(\displaystyle B\), then during a certain amount of time, water of mass \(\displaystyle m\) can be boiled. How much water can be boiled during the same amount of time when the voltage is applied across points \(\displaystyle B\) and \(\displaystyle C\) or across points \(\displaystyle C\) and \(\displaystyle A\)?
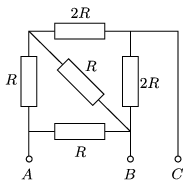
(4 pont)
solution (in Hungarian), statistics
P. 4969. Two flat coils, the symmetry axis of which coincide, are at a distance of \(\displaystyle h\) from each other, as shown in the figure. The number of turns of the coils are \(\displaystyle N_1\) and \(\displaystyle N_2\), their radii are \(\displaystyle R\) and \(\displaystyle r\) (\(\displaystyle r\ll R\)), and the values of the current flowing in them are \(\displaystyle I_1\) and \(\displaystyle I_2\), respectively. What is the force exerted between the two coils?
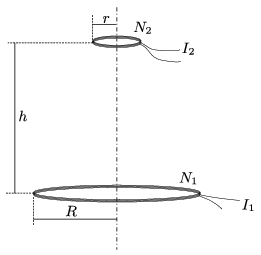
(6 pont)
Upload your solutions above.
