KöMaL Problems in Physics, February 2018
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'M'Deadline expired on March 12, 2018. |
M. 375. Measure how the force exerted by the prongs of a clothes peg depends on the angle between the prongs.
(6 pont)
 |
Problems with sign 'G'Deadline expired on March 12, 2018. |
G. 625. A spider is crawling at a uniform speed of 1 mm/s along the 1.5-metre minute hand of the tower clock, from the centre of the clock towards the end of the minute hand. The spider starts exactly at 12 o'clock.
\(\displaystyle a)\) What is the time shown by the clock, when the spider reaches the end of the minute hand?
Reaching the end of the minute hand the spider descends on a self-made thread attached to the end of the minute hand.
\(\displaystyle b)\) At what rate should the silk of the thread be made in order that the spider reach its starting position exactly at 13?
\(\displaystyle c)\) How far was the spider from the centre of the clock at 12:45?
(3 pont)
solution (in Hungarian), statistics
G. 626. What is the period of that simple pendulum of length \(\displaystyle \ell\) the thread of which bumps into a peg at the midpoint of the thread when the bob passes the equilibrium position? (The maximum angle that the thread differs from the vertical is small.)
(3 pont)
solution (in Hungarian), statistics
G. 627. At what height above the surface of the Earth will the gravitational force exerted on an object be exactly the same as that of on the surface of the Moon?
(3 pont)
solution (in Hungarian), statistics
G. 628. At the same time every morning it can be observed that Venus gets closer to the Sun. Where eventually will Venus pass the Sun, ,,in front of'' or ,,behind'' it?
(4 pont)
 |
Problems with sign 'P'Deadline expired on March 12, 2018. |
P. 5001. At the same time every morning it can be observed that Venus gets closer to the Sun. Where eventually will Venus pass the Sun, ,,in front of'' or ,,behind'' it?
(4 pont)
solution (in Hungarian), statistics
P. 5002. The centre of the Earth moves along a bit wavy elliptical path about the Sun.
\(\displaystyle a)\) What is the reason for this waviness?
\(\displaystyle b)\) Approximately what is the amplitude of the wave?
(4 pont)
solution (in Hungarian), statistics
P. 5003. Two simple pendulums, both having a length of \(\displaystyle \ell\) can swing in parallel, vertical planes, one right behind the other. Their shadows are projected perpendicularly to a wall, and every once in a while the shadows cross each other. Both pendulums are displaced by the same (small) angle and they are released at a time difference of \(\displaystyle t_0\). (\(\displaystyle t_0\) is smaller than the period of the pendulums.)
\(\displaystyle a)\) When do their shadows meet first?
\(\displaystyle b)\) When does the \(\displaystyle n\)-th encounter occur?
(4 pont)
solution (in Hungarian), statistics
P. 5004. The two ends of an 8-meter-long flexible thread are fixed at the same height at a distance of 4 m from each other. A 0.5 kg object is strung on the thread and can move frictionlessly along it. The thread is held tight and the object is released without initial speed such that the starting point and the ends of the thread are collinear.
What is the tension in the thread when the object is moving at the greatest speed?
(5 pont)
solution (in Hungarian), statistics
P. 5005. One of two alike cylinder-shaped, unopened soft drink cans is frozen in the freezer. Then they are released at the same time next to each other from the top of a slope.
Which one reaches the bottom of the slope first?
(3 pont)
solution (in Hungarian), statistics
P. 5006. A 200 g beach ball is strongly thrown downwards, onto the ground. When the ball is in its most compressed state, it touches the ground along a circle of diameter 10 cm, and the pressure in the ball is 110 kPa.
\(\displaystyle a)\) What is the greatest acceleration of the centre of mass of the ball, if the ground is dry and a little bit lumpy?
\(\displaystyle b)\) Would the value of the acceleration be different if the ground was wet and flat, and therefore there was no air left below that part of the ball which was in contact with the ground?
(The ambient air pressure is 100 kPa.)
(5 pont)
solution (in Hungarian), statistics
P. 5007. A laser beam is incident on a prism of vertex angle of \(\displaystyle 70^\circ\). The angle of incidence of the beam is the same as the angle at which the ray emerges from the prism. The laser beam is deflected from its original direction by an angle of \(\displaystyle 50^\circ\).
What is the refractive index of the material of the prism?
(3 pont)
solution (in Hungarian), statistics
P. 5008. A sample of monatomic gas is heated in such a way that during the process its molar heat capacity is the same as the universal gas constant \(\displaystyle R\). By what factor does the volume of the gas change if its temperature is doubled?
(5 pont)
solution (in Hungarian), statistics
P. 5009. A very thin thread pendulum of length \(\displaystyle \ell=0.8\) m is placed in vacuum. The pendulum is also in a region of uniform, horizontal magnetic field of induction \(\displaystyle B=2\) T; it is displaced horizontally in the plane which is perpendicular to the induction \(\displaystyle \boldsymbol B\), and then released without initial speed, as shown in the figure.
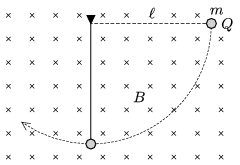
\(\displaystyle a)\) What amount of charge should the pendulum bob of mass \(\displaystyle m=0.1\) g be given in order that the tension in the thread when the bob is at the lowermost point of its path is 99% of the value of the tension without magnetic field?
\(\displaystyle b)\) What is the ratio of the values of the tension in the case of two consecutive passes?
(4 pont)
solution (in Hungarian), statistics
P. 5010. In a cyclotron the frequency of the voltage used to accelerate protons is 10 MHz. What is the necessary frequency when deuteron, singly ionised helium or doubly ionised helium atoms are accelerated?
(4 pont)
solution (in Hungarian), statistics
P. 5011. The two thinnest strings of a steel-string guitar (E and B) are made of great tensile strength steel. The thinner E string is overstrained until its pitch reaches sound G (a whole tone below the 440 Hz normal A sound) and it snaps.
\(\displaystyle a)\) At which sound would string B snap if it was also overstrained and it was made of the same tensile strength steel as string E?
\(\displaystyle b)\) What was the tensile strength of the material of string E?
\(\displaystyle c)\) The strings which have been used for a long time usually break at the bridge or at the tuning peg. Why?
\(\displaystyle d)\) From what other materials could the strings be made? Look for appropriate materials on the Internet or in tables.
The length of the oscillating part of the string is 64 cm, the density of the material of the steel string is \(\displaystyle 7.8 \cdot 10^3~\rm kg/m^3\).
(6 pont)
Upload your solutions above.
