A KöMaL 2018. márciusi fizika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
M-jelű feladatokA beküldési határidő 2018. április 10-én LEJÁRT. |
M. 376. Egy félliteres, vízzel teletöltött műanyag palackot a kupakján átmenő, a szimmetriatengelyére merőleges vízszintes tengely körül ingaként meglengetünk. Mérjük meg az inga lengésidejét különböző kezdeti kitérések esetén! Változik-e az eredmény, ha a vizet megfagyasztjuk?
Közli: Gnädig Péter, Vácduka
(6 pont)
 |
G-jelű feladatokA beküldési határidő 2018. április 10-én LEJÁRT. |
G. 629. Naszreddin Hodzsa vállára vette nehéz táskáját, úgy szállt fel a szamarára. Megkérdezték tőle, miért nem rakja a táskát a szamarára? Ezt válaszolta: ,,Az bizony állatkínzás lenne, épp elég nehéz vagyok én is a szegény párának.''
\(\displaystyle a)\) Miért hibás ez a válasz?
\(\displaystyle b)\) Rajzoljuk fel a történetben szereplő testekre ható erőket!
(3 pont)
G. 630. Miért homorú egy forgó edényben lévő víz felülete?
(3 pont)
G. 631. 30 g tömegű rézhuzal végeire 1,2 V feszültséget kapcsolunk, ennek hatására 2 A erősségű áram folyik át rajta. Mekkora feszültséget kell kapcsolnunk egy ugyancsak 30 g tömegű, kétszer olyan hosszú rézhuzalnak a végeire, hogy azon is 2 A erősségű áram folyjon keresztül?
(3 pont)
G. 632. Egy 900 km/h sebességgel haladó repülőgép másodpercenként 4 liter üzemanyagot (kerozint) használ fel. Mekkora utat tesz meg percenként az az autó, amelyik 100 kilométerenként 6,4 liter benzint fogyaszt, és 5 óra alatt annyi benzinre van szüksége, amennyi kerozint kilométerenként fogyaszt a repülőgép?
Közli: Tornyos Tivadar Eörs, Budapest
(4 pont)
 |
P-jelű feladatokA beküldési határidő 2018. április 10-én LEJÁRT. |
P. 5012. A phjongcshangi téli olimpián a magyar férfi rövidpályás gyorskorcsolyaváltó 5000 méteren 6 perc 31,971 másodperces rekordidővel olimpiai bajnok lett. A 111,12 m hosszú rövidpályás gyorskorcsolyapálya két 8,5 m sugarú félkörből és az azok végpontjait összekötő egyenes szakaszokból áll. Becsüljük meg, mekkora szögben dőlnek be a korcsolyázók a kanyarokban!
Közli: Frei Zsolt, Budapest
(4 pont)
P. 5013. Az ábrán látható, \(\displaystyle R=1\) m sugarú gyűrűből és könnyű, kicsi kerekekkel felszerelt kiskocsiból álló szerelvény tömege \(\displaystyle m\). A gyűrű aljába egy szintén \(\displaystyle m\) tömegű, pontszerű testet helyezünk. A testet pillanatszerűen \(\displaystyle v_0\) sebességgel elindítjuk. Mekkora \(\displaystyle v_0\), ha a kocsi éppen felemelkedik a talajtól, amikor a test a gyűrű legfelső pontjába kerül? A súrlódás mindenütt elhanyagolható.
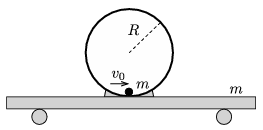
Közli: Berke Martin, Zalaegerszegi Zrínyi M. Gimnázium
(5 pont)
P. 5014. Mekkora sebességgel kellene fellőni egy lövedéket a Holdon, hogy emelkedési magassága elérje a Hold sugarának \(\displaystyle p\) százalékát? Legyen először \(\displaystyle p=1\), azután \(\displaystyle p=10\), végül \(\displaystyle p=100\). Mindhárom esetben 2 értékes jegy pontossággal adjuk meg az eredményt!
Példatári feladat nyomán
(4 pont)
P. 5015. Az 55 Cancri nevű csillag tömege és átmérője megegyezik a Napéval. Legbelső bolygója, a Janssen keringési ideje mindössze 17,76 óra. Adjuk meg a csillag és a bolygó átlagos távolságát csillagászati egységben, amely a Nap és a Föld átlagos távolsága!
Közli: Simon Péter, Pécs
(4 pont)
P. 5016. Egy homogén tömegeloszlású rúd fekszik a vízszintes asztallapon. A rudat az egyik végén ható, a rúdra mindenkor merőleges erővel lassan függőleges helyzetbe akarjuk hozni. Legalább mekkora a súrlódási együttható a rúd és az asztallap között, ha a rúd a felállítás közben nem csúszik meg?
A Kvant nyomán
(5 pont)
P. 5017. Egy 10 literes bojlerbe olyan kis teljesítményű fűtőtestet építettek, hogy az ne legyen képes a vizet forráspontig melegíteni. A víz teljes felmelegedése után a fűtést kikapcsolva a víz hőmérséklete az első percben \(\displaystyle 1~{}^\circ\)C-kal csökken. Mekkora a fűtőtest teljesítménye, ha a bojler vízértéke 3 kg?
Versenyfeladat nyomán
(4 pont)
P. 5018. Ha a tüzelőt nem kályhában égetjük el, hanem egy hőerőgép tűzterében, a hőerőgéppel pedig egy hőszivattyút hajtunk meg, akkor a lakásba több hő juthat, mint amennyi a tüzelő elégetésekor keletkezik. Legyen a lakás a hőerőgép alsó hőtartálya, valamint a hőszivattyú felső hőtartálya. A hőszivattyú alsó hőtartálya lehet az utca levegője. Tegyük fel, hogy a hőerőgép hatásfoka \(\displaystyle \eta_1\), a hőszivattyúról pedig tételezzük fel, hogy hőerőgépként működtetve \(\displaystyle \eta_2\) hatásfokú lenne. Számítsuk ki, hogy a tüzelő elégetésekor felszabaduló hőnek hányszorosa kerül így a lakásba!
Közli: Radnai Gyula, Budapest
(5 pont)
P. 5019. Függőleges irányú, homogén, \(\displaystyle 2\cdot 10^{-3}\) T indukciójú mágneses mezőben a vízszintessel \(\displaystyle 30^\circ\)-os szögben mozog egy 1,5 eV energiájú elektron. Hányszor metszi mozgása közben ugyanazt az indukcióvonalat, míg 20 cm-t süllyed?
Közli: Holics László, Budapest
(4 pont)
P. 5020. Egy ernyőn lévő kör alakú nyílást az ernyőre merőleges, koherens lézerfénnyel világítunk meg. Az ernyőtől távolabb, az optikai tengelyre merőlegesen egy CCD-érzékelő lemezt helyeztek el. Hány százalékkal csökken az optikai tengelyen lévő pixel megvilágítása (a rá eső fény intenzitása), ha a nyílás 1/6-át egy átlátszatlan, körcikk alakú lemezzel eltakarjuk?
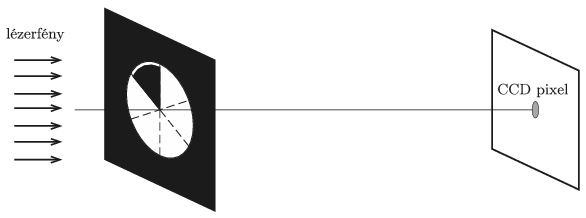
Példatári feladat nyomán
(5 pont)
P. 5021. Legfeljebb mekkora energiára tehet szert egy – kezdetben állónak tekinthető – elektron, ha egy 1 MeV mozgási energiájú másik részecskével ütközik, amennyiben ez a részecske
\(\displaystyle a)\) proton;
\(\displaystyle b)\) elektron;
\(\displaystyle c)\) pozitron?
Közli: Fröhlich Georgina, Budapest
(4 pont)
P. 5022. Két fonál közül az egyik \(\displaystyle L\), a másik \(\displaystyle 2L\) hosszúságú. A fonalak végein azonos, \(\displaystyle m\) tömegű, pontszerűnek tekinthető testek vannak. A testeknek azonos, \(\displaystyle Q\) töltése van. Egyensúly esetén mekkora szöget zárnak be a közös pontban rögzített fonalak?
Adatok: \(\displaystyle L=20\) cm, \(\displaystyle m=1\) g, \(\displaystyle Q=2{,}8\cdot 10^{-7}\) C.
Közli: Zsigri Ferenc, Budapest
(6 pont)
A fizika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

