A KöMaL 2018. áprilisi informatika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
I-jelű feladatokA beküldési határidő 2018. május 10-én LEJÁRT. |
I. 454. A szólánc kedvelt nyelvi játék. A játék során úgy kell szavakat egymás után mondani, hogy az előző szó utolsó betűjével kezdődjön a következő szó. Ebben a feladatban egy kész szólánc összekevert szavait kell a játék szabályainak megfelelően újra sorrendbe állítani.
Készítsünk programot i454 néven, amely a bemeneten megadott \(\displaystyle N\) szó mindegyikét felhasználva a szóláncot előállítja. Minden szó a szóláncban egyszer szerepelhet és kell is, hogy szerepeljen. Több lehetséges megoldás esetén elegendő egyet megadni.
A program standard bemenetének első sorában a szavak \(\displaystyle N\) (\(\displaystyle 2\le N\le 500\)) számát és az ezt követő \(\displaystyle N\) sorban a szavakat (ékezetmentesek és nagybetűsek) adjuk meg. A program a standard kimenetre írja ki a szóláncot. A szavakat szóközzel elválasztva sorolja fel.

Beküldendő egy tömörített i454.zip állományban a program forráskódja és rövid dokumentációja, amely megadja, hogy a forrásállomány melyik fejlesztői környezetben fordítható.
(10 pont)
I. 455. (É). Mobiltelefon-előfizetések számát sorolja fel 2000 és 2015 között, ezer lakosra megadva a következő weboldal: https://www.ksh.hu/docs/hun/xstadat/xstadat_eves/i_int074.html (utolsó letöltés: 2018. január 6.). A feladat ezen adatok feldolgozása lesz táblázatkezelő program segítségével.
1. Töltsük be a mobilelofizetesek.txt szövegfájlt a táblázatkezelő egy munkalapjára az A1-es cellától kezdődően. Munkánkat i455 néven mentsük el a táblázatkezelő alapértelmezett formátumában.
2. Vizsgáljuk meg országonként, hogy egyik évről a következőre, hány ezer fővel nőtt a felhasználók száma. Ennek függvényében adjuk meg, hogy az adott országban mekkora volt az átlagos növekedés. Végül az U oszlop egy cellájában határozzuk meg, hogy az összes országot figyelembe véve mekkora az átlagos évenkénti növekedés.
3. Az R oszlopban adjuk meg százalékban kifejezve, hogy mennyi az adott ország éves növekedésének átlaga az összes ország átlagához viszonyítva.
4. Az U oszlop egy cellájában határozzuk meg, hogy melyik az az ország, ahol a legnagyobb eltérés mutatkozott a felhasználók száma között valamely két egymást követő évet viszonyítva egymáshoz.
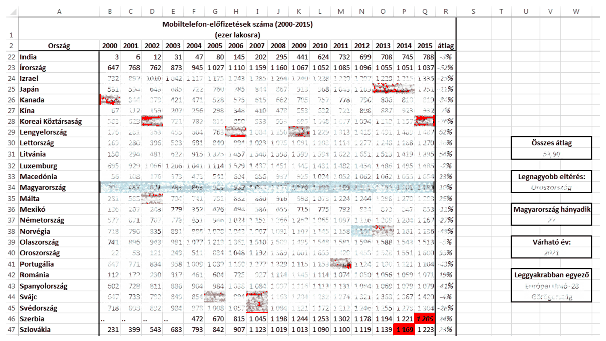
5. Az U oszlop egy újabb cellájában adjuk meg, hogy Magyarország – a 2015-ös évet figyelembe véve – hányadik volt a mobiltelefon-előfizetéssel rendelkezők számának rangsorában.
6. Az előző eredmények alatt egy új cellában határozzuk meg, hogy várhatóan melyik lesz az az év, amikor minden ország eléri az 1 millió előfizetőt, ha az adatok az eddigi országonkénti növekedést követik (tételezzük fel, hogy az előfizetések száma független a népességtől, és a népesség meghaladja az 1 millió főt mindegyik országban).
7. Feltételes formázást használva jelöljük világoskék színnel és félkövér stílussal az évenkénti magyarországi értékeket és az adott évben a magyarországi értékkel egyező értékeket. A magyarországi értékhez legközelebb eső, nála nagyobb számértéket jelöljük félkövér, dőlt betűstílussal és pirosan kitöltött cellával, az annál kisebb, hozzá legközelebb eső értéket félkövér stílussal, piros kitöltéssel.
8. A 6. pont eredményét tartalmazó cella alatt határozzuk meg, hogy melyik az az ország, vagy országok, amik a leggyakrabban voltak a magyarországi értékek közelében az összes évet tekintve.
9. Készítsünk diagramot külön diagram típusú munkalapra, ahol ábrázoljuk a magyarországi, és a hozzá legközelebb álló két ország értékeit az évek függvényében a minta alapján.
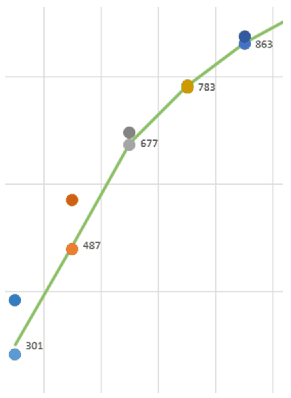
10. A diagramot és a táblázatot a minta alapján formázzuk úgy, hogy a táblázat első két sora mindig látható legyen.
Beküldendő egy tömörített i455.zip állományban a megoldást adó táblázatkezelő munkafüzet és egy rövid dokumentáció, amely megadja a felhasznált táblázatkelő nevét és verzióját.
Letölthető állomány: mobilelofizetesek.txt.
(10 pont)
I. 456. A képek tárolására igen sokféle fájltípus alakult ki a tárolásmóddal, a méretekkel szembeni különböző elvárások miatt. A szöveges módon tárolt, tömörítés nélküli képek nagyméretű fájlokat eredményeznek. Szerkezetük egyszerű és a legtöbb képnézegető, képszerkesztő képes megjeleníteni őket.
Készítsünk programot i456 néven, amely egy .pgm kiterjesztésű (portable graymap format), 8-bites, szürkeárnyalatos képet állít elő, amely egy arkhimédészi spirált ábrázol. A kép négyzet alakú legyen és a spirál középen helyezkedjen el. A hátteret állítsuk fehérre és a spirál színét, belülről kifelé, menetenként feketétől fokozatosan a világosszürkéig változtassuk.
A program standard bemenetének első sorában a négyzet alakú kép \(\displaystyle N\) (\(\displaystyle 10\le N\le 1000\)) oldalhosszát, a szürkeárnyalatok \(\displaystyle K\) (\(\displaystyle 1\le K\le 255\)) számát, második sorában a spirál meneteinek \(\displaystyle M\) (\(\displaystyle 1\le M\le 10\)) számát és \(\displaystyle L\) (\(\displaystyle 1\le L\le 10\)) vonalvastagságát adjuk meg.
A program írja a standard kimenetre az előállított pgm típusú képfájl szöveges tartalmát, amelyet, ha fájlba irányítunk át, akkor utána képnézegetővel az ábra megtekinthető.

Értékelés: a megoldás lényegét leíró dokumentáció 1 pontot ér. További 9 pont kapható arra a programra, amely a korlátoknak megfelelő bemenetekre helyes kimenetet ad. Részpontszám kapható arra a programra, amely vonalvastagságot, vagy színátmenetet nem kezel.
Beküldendő egy tömörített i456.zip állományban a program forráskódja és rövid dokumentációja, amely megadja, hogy a forrásállomány melyik fejlesztői környezetben fordítható.
(10 pont)
 |
I/S-jelű feladatokA beküldési határidő 2018. május 10-én LEJÁRT. |
I/S. 26. Informatikusok a 21-es játék egy módosított, digitalizált változatával játszanak. Nem kártyával, hanem számítógép segítségével. A gép a játék megkezdésekor mindegyik játékosnak előállít egy 64 hosszú, 1 és 9 közötti egészeket tartalmazó sorozatot – ezek lesznek egy-egy játékos ,,felhúzható lapjai''. A játék körökből áll, melyek során minden játékos ,,húzhat'' a neki sorsolt lapok közül, vagy ,,dobhat'' a kezében található lapok közül. Fontos szabály, hogy húzni vagy dobni csak pontosan 1, 2, 4 vagy 8 számú lapot szabad. A játékos a dobáshoz bármely kártyalapokat kiválaszthatja a kezéből, de húzni csak a számsorozat sorrendben következő, megfelelő darabszámú lapját szabad. A játékosok kezdetben egy lappal sem rendelkeznek. Az a játékos győz, akinek elsőként lesz a kezében az adott körben történt húzása vagy dobása után 21 a számok összege. A játék során a kézben tartott lapok összege meghaladhatja a 21-et, ez nem jelent kiesést.
Természetesen minden játékos vihetett magával egy programozható eszközt, és annak segítségével is játszhatott. Készítsünk olyan programot, amely a 64 egész ismeretében meghatározza az egyes körökben a húzások és dobások stratégiáját úgy, hogy a lehető legkevesebb kört kelljen a játékosnak játszania a 21 eléréséhez.
A megoldást adó program a standard bemenetről olvassa be a 64 egész számot, majd írja ki a standard kimenet első sorába a 21 eléréséhez szükséges legkevesebb körök számát, illetve a következő sorokban a játékos kezében lévő kártyákat növekvő sorrendben. Amennyiben a 21 nem elérhető a 64-es sorozatból szabály szerinti húzásokkal és dobásokkal, akkor a kimenet csak egy 0 legyen. Amennyiben azonos számú kör, de különböző húzások és dobások esetén is elérhető a 21, akkor bármelyik megoldás elfogadható.
Példa:
| Bemenet (nem teljes, de nem lényeges a további része) | Kimenet (a / jel sortörést jelöl) |
| 2 3 7 4 9 8 4 5 3 3 \(\displaystyle \ldots\) | 2 / 2 3 7 4 9 8 4 5 / 2 3 7 9 |
Értékelés: a megoldás lényegét leíró dokumentáció 1 pontot ér. További 9 pont kapható arra a programra, amely a korlátoknak megfelelő bemenetekre helyes kimenetet ad 1 másodperc futásidő alatt. Részpontszám kapható arra a programra, amely nem minden bemeneti érték esetén ad helyes eredményt 1 másodpercen belül.
Beküldendő egy is26.zip tömörített állományban a megoldást leíró dokumentáció és a program forráskódja.
(10 pont)
 |
S-jelű feladatokA beküldési határidő 2018. május 10-én LEJÁRT. |
S. 125. Egy bolygó felszínét teljesen lefedik a rajta található országok, melyeket egymástól határvonalak választanak el. Minden ország egy-egy összefüggő részén található a bolygónak. A határvonalak a bolygó felületén haladó görbék, találkozási pontjaikban határvárosok találhatók. Egy-egy határváros legalább kettő, de akár több ország határvonalainak a találkozási pontja. Minden országnak legalább két szomszédja, és legalább három határvárosa van. A határvonalak a határvárosokon kívül nem keresztezik egymást, és határváros sincs máshol, csak határvonalak találkozásánál.
Egy ország határvárosainak számát nevezzük az ország határszámának. Állapítsuk meg, hogy mennyi a bolygón az országok határszámának maximuma.
A határvárosokat pozitív egész számokkal, a határvonalakat a megfelelő határvárosok számából képzett számpárokkal jelöljük. A megoldást adó program a standard bemenet első sorából olvassa be a határvárosok \(\displaystyle V\) számát, illetve a határvonalak \(\displaystyle L\) számát, majd a következő \(\displaystyle L\) sor mindegyikéből egy-egy határvonalat megadó számpárt. A program írja a standard kimenetre a bolygón található országok határszámai közül a legnagyobbat.
Példa:

Korlátok: \(\displaystyle 4\le V\le 1000\).
Értékelés: a megoldás lényegét leíró dokumentáció 1 pontot ér. További 9 pont kapható arra a programra, amely a korlátoknak megfelelő bemenetekre helyes kimenetet ad 1 másodperc futásidő alatt. Részpontszám kapható arra a programra, amely csak kisebb bemeneti értékek esetén ad helyes eredményt 1 másodpercen belül.
Beküldendő egy s125.zip tömörített állományban a megoldást leíró dokumentáció és a program forráskódja.
(10 pont)
Figyelem!
Az informatika feladatok megoldásait ne e-mailben küldd be! A megoldásokat az Elektronikus munkafüzetben töltheted fel.

