KöMaL Problems in Physics, November 2018
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'M'Deadline expired on December 10, 2018. |
M. 381. Make a cylinder from a sheet of A4-size paper (or some part of it) by gluing it. Roll it down from the top of an inclined plane, which is on a table such that its lower end is just at the rim of the table.
Measure how far from the vertical projection of the rim of the table on the floor the cylinder reaches the floor. (The cylinder should roll without sliding.) How does this distance depend on the diameter of the cylinder? Compare your results with the horizontal displacement of a small object (e.g. a coin) which slides without rolling along the slope and falls from the end of the slope.
(6 pont)
 |
Problems with sign 'G'Deadline expired on December 10, 2018. |
G. 649. If we move in a steam bath (for example we begin to fan ourselves with the arms), then we feel the 40–60 \(\displaystyle {}^\circ\)C vapour much hotter, and it may feel like our skin is burning. Why?
(3 pont)
solution (in Hungarian), statistics
G. 650. Aaron played with his ruler and rubber. He put the small rubber to one end of the 30-cm long ruler and slowly slid the ruler along the tabletop, perpendicular to the rim of the table, such that the end of the ruler was sticking out from the table. He measured that when the ruler is sticking out more than 11 cm it falls down. What is the ratio of the masses of the ruler and the rubber?
(3 pont)
solution (in Hungarian), statistics
G. 651. On the hull of ocean liners there is a mark called the Plimsoll line. This shows the legal limit to which the ship may be loaded, indicating the maximum draft of the ship in specific water types and temperatures. (TF = Tropical Fresh Water; F = Fresh Water; T = Tropical Seawater; S = Summer Seawater; W = Winter Seawater; WNA = Winter North Atlantic.)
The topmost TF line marks the draft of the hull when the liner is in tropical fresh water (its density is 996 kg/m\(\displaystyle {}^3\)), whilst the F line below marks the maximum draft in case of fresh water in temperate zone (its density is 999 kg/m\(\displaystyle {}^3\)). On a specific ocean liner the distance between these two lines is 7 cm. What is the density of winter seawater if its mark on the hull of this liner is 21 cm below the topmost line?
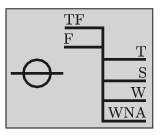
(4 pont)
solution (in Hungarian), statistics
G. 652. An object starts from rest and moves along a straight line such that its acceleration increases uniformly in time, from the value of zero it increases by 2 m/s\(\displaystyle ^2\) in each second. What is the speed of the object 4 s after it started to move?
(4 pont)
 |
Problems with sign 'P'Deadline expired on December 10, 2018. |
P. 5067. Two light springs, whose spring constants are \(\displaystyle D_1\) and \(\displaystyle D_2\) are put onto a frictionless rod. One end of each spring is fixed and the distance between their other ends is \(\displaystyle d\). There is also a small object of mass \(\displaystyle m\) on the rod, and with this small object one of the springs is compressed by \(\displaystyle x\), and then the object is released. How much time elapses until the object of mass \(\displaystyle m\) reaches its initial position? Does this time depend on the spring it was started from?
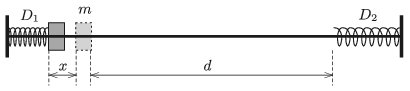
(4 pont)
solution (in Hungarian), statistics
P. 5068. A small comet of mass \(\displaystyle m\), which can be considered point-like, approaches a spherical planet of mass \(\displaystyle M\), and of radius \(\displaystyle R\) (\(\displaystyle m\ll M\)). The speed of the comet very far from the planet is \(\displaystyle v_0\), and if the gravitational field of the planet did not exert any force on the comet, it would pass the planet at a distance of \(\displaystyle d\) from the centre of the planet (\(\displaystyle d>R\)). What is the minimum value of \(\displaystyle v_0\), at which the comet does not hit the planet? (Apart from the planet and the comet, the gravitational fields of any other celestial objects can be neglected.)
(5 pont)
solution (in Hungarian), statistics
P. 5069. A solid cylinder of mass \(\displaystyle M\) and of radius \(\displaystyle R\) was placed onto a slope of angle of inclination of \(\displaystyle \alpha\). The cylinder is attached to the top end of the inclined plane by means of a horizontal thread as shown in the figure. Next to the object there is another cylinder of mass \(\displaystyle m\) and of radius \(\displaystyle r\). Friction between the two cylinders is negligible, and the cylinder of mass \(\displaystyle M\) is not rising. What is the least value of the coefficient of static friction between the slope and the cylinder of radius \(\displaystyle R\) if the cylinders do not slide on the slope?
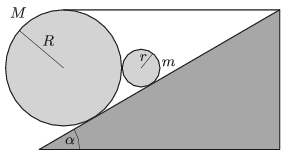
Data: \(\displaystyle \alpha=30^\circ\), \(\displaystyle R=3r\), \(\displaystyle M=3m\).
(5 pont)
solution (in Hungarian), statistics
P. 5070. There is a spring of spring constant \(\displaystyle D\) and of un-stretched length \(\displaystyle d\) in a cave of height \(\displaystyle \ell\). The spring is vertical, its mass is negligible and \(\displaystyle d<\ell\). One end of the spring is attached to the ceiling and the other is attached to the ground of the cave as shown in the figure.

A small bat of mass \(\displaystyle m\) flies to the midpoint of the spring, clings to the spring, and executes a complicated oscillatory motion driven by the spring. (Not any part of the spring gets loose during the motion of the bat.)
\(\displaystyle a)\) Where will the bat be when the oscillation is ceased? (The spring obeys Hooke's law even in the case of very big extensions.)
\(\displaystyle b)\) From this point the bat carefully climbs up to its original height of \(\displaystyle \ell/2\) measured from the ground. What is the least amount of work performed by the bat during its climb?
(5 pont)
solution (in Hungarian), statistics
P. 5071. A load hanging on an elastic thread is pulled downwards by a force which is increased slowly from 0. The thread breaks at a force of \(\displaystyle F_1\). What is the least value of the force at which the thread breaks, if the force immediately takes that value, and does not change after it?
(5 pont)
solution (in Hungarian), statistics
P. 5072. The diameter of a neon atom is 0.32 nm. Estimate that when the temperature of the neon gas is \(\displaystyle 0~{}^\circ\)C and its pressure is 1 atm
\(\displaystyle a)\) by what factor of the average distance between the atoms of the gas is greater than the diameter of a single neon atom?
\(\displaystyle b)\) by what factor of the average thermal speed of the atoms is greater than the speed of sound in the gas?
(4 pont)
solution (in Hungarian), statistics
P. 5073. The linear charge density of a vertical very long (``infinitely'' long) straight insulating thread is \(\displaystyle \lambda=8\cdot10^{-7}\) C/m. A small metal ball of mass \(\displaystyle m=2\) g and of charge \(\displaystyle q=7\cdot10^{-8}\) C, is hung by a very thin insulating filament of length \(\displaystyle \ell=10\) cm, at a distance of \(\displaystyle d_0=5~\)cm from the thread. Without any push the ball is released when the filament is vertical.
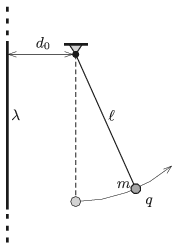
\(\displaystyle a)\) How far will the metal ball move from the thread?
\(\displaystyle b)\) What is the angle between the vertical and the filament when the ball moves at its maximum speed? What is this maximum speed?
\(\displaystyle c)\) What force is exerted on the support when the ball is moving at its greatest speed?
(5 pont)
solution (in Hungarian), statistics
P. 5074. Each side of a regular hexagon consists of a piece of wire of resistance \(\displaystyle R\). From one of the vertices of the hexagon there are wires leading diagonally to the other three not adjacent vertices of the hexagon. These wires are made of the same type of material as the wires of the sides. What is the equivalent resistance between this vertex and the opposite one?
(4 pont)
solution (in Hungarian), statistics
P. 5075. Parallel to each other there are four thin lenses along the same optical axis, as shown in the figure. The radii of the curvatures of each lens are 5 cm, and 10 cm. Two of the lenses are air lenses which are in glass of refractive index of \(\displaystyle n=1.5\), and the other two lenses are made of glass of the same refractive index.
In the glass there is a point-like light source on the optical axis at a distance of 60 cm from the convex meniscus lens. On the other side of this lens at a distance of 30 cm there is the concave meniscus air lens. The boundary of the glass is at a distance of 10 cm from this concave meniscus air lens. From the boundary of glass at a distance of 10 cm there is the convex meniscus glass lens and the fourth (concave meniscus) glass lens is at a distance of 20 cm from the third one.
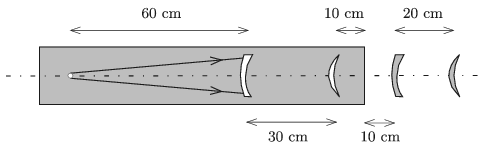
Where is the image of the light source created by the four lenses?
(4 pont)
solution (in Hungarian), statistics
P. 5076. A monochromatic laser beam of wavelength \(\displaystyle \lambda\) is incident on a diffraction grating. The beam is perpendicular to the slits of the grating, and encloses an angle of \(\displaystyle 45^\circ\) with the plane of the diffraction grating. Determine the number and the direction of the maxima of the diffraction pattern, if the grating spacing is
\(\displaystyle a)\) \(\displaystyle d=\lambda\);
\(\displaystyle b)\) \(\displaystyle d=5\lambda\).
(5 pont)
solution (in Hungarian), statistics
P. 5077. There is a piston having good thermal conductivity in the middle of a cuboid-shaped container having thermally insulating walls. On the left side of the piston there is a sample of air of volume \(\displaystyle V_0\), whilst on the right side there is a sample of air of volume \(\displaystyle V_0/2\) at a pressure of \(\displaystyle p_0=76~{\rm Hgcm}\approx 10^5\) Pa, and a mercury column of height \(\displaystyle h=38~\)cm. The total width of the container is \(\displaystyle 2h\) (not considering the width of the piston), and its height is also \(\displaystyle 2h\).
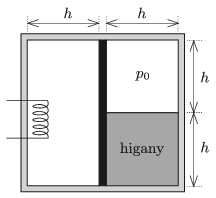
By means of a built-in electric heater the left side of the system is slowly heated. The temperatures of the two samples of gases are the same at any time. At most what can the displacement of the piston be, if the expansion of the container, the piston and the mercury is neglected?
(6 pont)
Upload your solutions above.
