KöMaL Problems in Physics, January 2019
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'M'Deadline expired on February 11, 2019. |
M. 383. Place a sand-glass on a slope, and measure how long it takes for the sand to run down through the hole of the sand-glass as a function of the angle of the slope.
(6 pont)
 |
Problems with sign 'G'Deadline expired on February 11, 2019. |
G. 657. An aquarium with an open top has a shape of a square-based right prism. Its base and face walls are made of 1 cm thick glass sheet. The inner height of the aquarium is 20 cm, and each of its inner base edge is 30 cm long.
The aquarium is filled with water. The water flows into the aquarium from a tap at a rate of 5 cm\(\displaystyle {}^3\) per second.
\(\displaystyle a)\) How long does it take to fill the half of the aquarium with water?
\(\displaystyle b)\) What is the weight of the halfway filled aquarium?
(The density of water is 1000 kg/m\(\displaystyle {}^3\), and the density of glass is 2500 kg/m\(\displaystyle {}^{3}\).)
(3 pont)
solution (in Hungarian), statistics
G. 658. Six forces are exerted on the same body at the same time: \(\displaystyle F_1=1\) N, \(\displaystyle F_2=2\) N, \(\displaystyle F_3=3\) N, \(\displaystyle F_4= 4\) N, \(\displaystyle F_5=5\) N and \(\displaystyle F_6=6\) N. The forces are all in the same plane and the angles between two adjacent forces are \(\displaystyle 60^\circ\) (i.e. the consecutive rotations of the forces are always \(\displaystyle 60^\circ\) in the same direction).
\(\displaystyle a)\) What is the vector sum of the six forces?
\(\displaystyle b)\) How should the magnitude or maybe as well the direction of force \(\displaystyle F_{2}\) be changed in order for the object to be in equilibrium?
(3 pont)
solution (in Hungarian), statistics
G. 659. We have two sets of Christmas lights, both rated at 50 W and 230 V. In one of the sets there are 50 bulbs, whilst in the other there are 100 bulbs connected in series.
\(\displaystyle a)\) In which set is the current greater?
\(\displaystyle b)\) In which set is the resistance of a bulb greater?
\(\displaystyle c)\) Will the power of the set containing 100 bulbs increase or decrease if 10 of its bulbs are changed to ten bulbs from the other set? (Assume that none of the bulbs blow out.)
(3 pont)
solution (in Hungarian), statistics
G. 660. One end of an initially 2 m long horizontal elastic band is tied to a wall, and a snail is moving along it at a speed of 1 m/h. The snail starts from the wall, and the band is stretched by 1 m from the end of the band at the end of each hour. How much time elapses until the snail reaches the end of the band?
(4 pont)
 |
Problems with sign 'P'Deadline expired on February 11, 2019. |
P. 5089. The frictionless trajectory shown in the figure consists of two circular arcs. A tiny object starts to slide from point \(\displaystyle A\) along the trajectory with a very small initial speed. How long does it take for the tiny object to reach the right end of the curved path (point \(\displaystyle B\))?
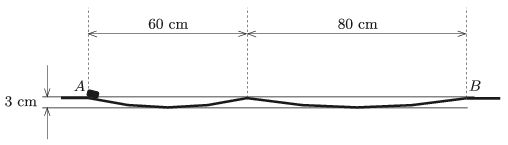
(4 pont)
solution (in Hungarian), statistics
P. 5090. There is a cube-shaped box of mass \(\displaystyle m\) on a horizontal floor. A thin, uniform rod of also mass \(\displaystyle m\) is leant against one of the faces of the cube touching it at its centre. Initially both of the objects are fixed. The angle between the ground and the rod is \(\displaystyle \alpha=45^\circ\).
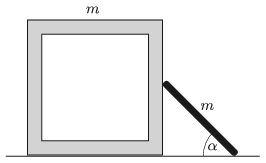
What is the initial acceleration of the box at which it starts to move when the objects are released? (Friction is negligible everywhere.)
(5 pont)
solution (in Hungarian), statistics
P. 5091. At STP the density of air is approximately 0.0013 g/cm\(\displaystyle {}^{3}\), whilst the density of liquefied air is approximately \(\displaystyle 0.87\) g/cm\(\displaystyle {}^{3}\).
\(\displaystyle a)\) Estimate the number of "air molecules" in 1 cm\(\displaystyle {}^{3}\) air at STP and at its liquefied state.
\(\displaystyle b)\) Estimate the mass of an "air molecule".
(3 pont)
solution (in Hungarian), statistics
P. 5092. An easily moveable piston of mass \(\displaystyle m\) and cross sectional area \(\displaystyle A\) is made of a material which poorly conducts heat. The piston divides a horizontal, fixed, and thermally insulated cylinder into two parts, having the same volume of \(\displaystyle V_{0}\). There is the same amount of helium gas in the two parts, at the pressure of \(\displaystyle p_{0}\).
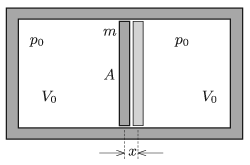
The piston is displaced a bit, and then released. What is the period of the resulting oscillation?
(5 pont)
solution (in Hungarian), statistics
P. 5093. In this problem, the experiment carried out on a space station in weightlessness is about a special "orbital speed" and "escape velocity". A charged sphere, made of some insulating material, has a radius \(\displaystyle R =10\) cm, and charge \(\displaystyle Q = -10^{-7}\) C (uniformly distributed). We would like to know the orbital speed of an object of mass \(\displaystyle m = 0.1\) g, and of charge \(\displaystyle q=2\cdot10^{-9}\) C when it is on a circular orbit 2 cm from the surface of the sphere; and we would also like to find the escape velocity of the same object, when it is launched from a point 2 cm from the surface of the sphere.
(4 pont)
solution (in Hungarian), statistics
P. 5094. Three point-like objects, each having mass of \(\displaystyle m = 1\) g and charge of \(\displaystyle Q=3.1\cdot 10^{-7}\) C, are attached to one of the ends of three insulating threads of length \(\displaystyle L = 20\) cm (one to each thread). The other ends of the threads are fixed at a common point. Initially the threads were tight and the angle between the vertical and a thread was \(\displaystyle \alpha=30^\circ\), and the small objects were at the vertices of an equilateral triangle. Then the small objects were released at the same instant.
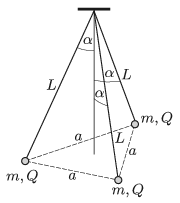
\(\displaystyle a)\) What is the angle between the threads and the vertical when the objects have the greatest speed?
\(\displaystyle b)\) What is the greatest speed of the objects?
(5 pont)
solution (in Hungarian), statistics
P. 5095. Two resistors of resistance values \(\displaystyle R_{1}\) and \(\displaystyle R_{2}\) are connected in series and their equivalent resistance is \(\displaystyle R_{1}+R_{2}\). Two other resistors of resistance \(\displaystyle R\) are connected in the circuit, one of them and \(\displaystyle R_{1}\) are connected in parallel, whilst the other one and \(\displaystyle R_{2}\) are connected in series. Is there a value of \(\displaystyle R\) such that the equivalent resistance of the whole circuit remains \(\displaystyle R_{1}+R_{2}\)?
(4 pont)
solution (in Hungarian), statistics
P. 5096. A small, luminous, circular sheet of radius 2 mm is at a distance of 10 cm from the centre of a uniform, solid glass sphere of radius 4 cm. The plane of the circular sheet is perpendicular to the optical axis, i.e. to the line connecting the centres of the sphere and the circular sheet. Where is the image of the circular sheet formed by the glass sphere and what is the size of the image? (The refractive index of glass is 1.5, and only the rays which are nearly parallel to the optical axis play a role in the image formation.)
(5 pont)
solution (in Hungarian), statistics
P. 5097. There are three thin slits on an opaque sheet such that the distance between two adjacent slits is \(\displaystyle d\). The width of the slit at the middle is \(\displaystyle \sqrt 2\) times bigger than that of the slits on the sides. A laser beam of wavelength \(\displaystyle \lambda\) is incident on the slits, and perpendicular to the sheet. The diffraction pattern is observed on a screen at a distance of \(\displaystyle L\). What is the distance on the screen between the zero-order maximum and the first zero-intensity point? (Suppose that \(\displaystyle \lambda\ll d\ll L\).)
(5 pont)
solution (in Hungarian), statistics
P. 5098. The broadening of spectral lines of stars have many different reasons, among them one is the rotation of the star. In the spectrum of a star the spectral line of hydrogen named H\(\displaystyle \delta \) (belonging to the Balmer series) has a wavelength of 410.174 nm measured under laboratory circumstances, and is observed to be broadened in the interval between 410.171 nm and 410.177 nm.
\(\displaystyle a)\) What is the period of the rotation of the star about its axis, if its diameter is \(\displaystyle 1.4\cdot 10^9\) m? Suppose that the axis of rotation is perpendicular to the direction from which the star is observed, and that the broadening is mainly due to the rotation of the star.
\(\displaystyle b)\) What could we deduce about the motion of the star, if the wavelength of the broadened spectral line was observed to be in the interval of 410.176 nm and 410.182 nm?
(5 pont)
solution (in Hungarian), statistics
P. 5099. A roller coaster car is moving along a vertical circular loop such that it uses its own engine and brakes to keep its speed constant. What should its least speed be in order that it follows the circular loop of radius \(\displaystyle R\) without slipping, if the coefficient of static friction is \(\displaystyle \mu\)? Where would it slip if its speed was a bit smaller than this value? The car is small enough compared to the radius of the loop.
(6 pont)
Upload your solutions above.
