KöMaL Problems in Physics, February 2019
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'M'Deadline expired on March 11, 2019. |
M. 384. Determine the efficiency of an electric kettle of known power rating, as a function of the mass of the water in it.
(6 pont)
 |
Problems with sign 'G'Deadline expired on March 11, 2019. |
G. 661. Three types of liquid, which do not mix with each other, are poured into a graduated cylinder: 100 g water of density 1000 kg/m\(\displaystyle {}^3\), 200 g oil of density 0.8 g/cm\(\displaystyle {}^3\), and mercury, such that the graduated cylinder of volume 400 cm\(\displaystyle {}^3\) and of height 40 cm is fully filled. How many grams of mercury was poured into the cylinder? At what height, measured from the bottom of the cylinder, are the boundary layers which separate the different liquids? (The density of mercury is \(\displaystyle 13\,600\) kg/m\(\displaystyle {}^3\).)
(3 pont)
solution (in Hungarian), statistics
G. 662. A disc with greater radius and two smaller cylinder are attached to each other concentrically; the assembly is shown in figures \(\displaystyle (a)\) and \(\displaystyle (b)\). Two pieces of cords were wrapped around the cylinders, and their ends are moved horizontally at constant speed of \(\displaystyle v\), with the help of a rod.
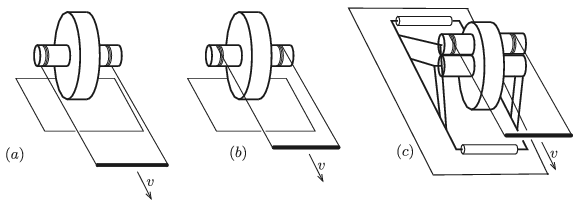
In the \(\displaystyle (c)\) case, there is another cylinder, which can rotate freely, above the cylinder on the original device. The cylinders have the same radius, and touch each other tightly. A rod structure is attached to the cylinders in order to prevent them from falling. A piece of cord is wrapped around the top cylinder and the end is again pulled at a constant speed of \(\displaystyle v\). The discs do not slip on the ground and the cylinders do not slip on each other.
In what direction will the centre of the disc move in each case? Will the speed of the centre of the disc be greater or smaller than \(\displaystyle v\) in each case?
(3 pont)
solution (in Hungarian), statistics
G. 663. There are two filament lamps, a battery and a double switch in the figure. The switch changes two contacts at the same time when it is turned. Plan a circuit (that is, draw the wires) using the given components in which the two lamps are connected in series at one position of the switch, and when the switch is turned, then the lamps are connected in parallel.
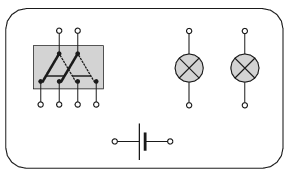
(3 pont)
solution (in Hungarian), statistics
G. 664. In which case are we closer to the Sun on the same day of the year: at new-moon or at full-moon? Estimate the difference between the distances at the two cases?
(4 pont)
 |
Problems with sign 'P'Deadline expired on March 11, 2019. |
P. 5100. Two cannons fire a ball at the same time towards each other from points \(\displaystyle A\) and \(\displaystyle B\) as shown in the figure. The nozzle speed of the ball fired from the cannon at \(\displaystyle A\) is 40 m/s, whilst the nozzle speed of the ball fired from the cannon at \(\displaystyle B\) is 60 m/s. Do the two balls collide? If yes, where and when? If not, where do the balls hit the ground?
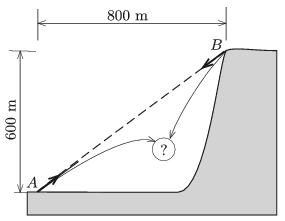
(4 pont)
solution (in Hungarian), statistics
P. 5101. A space ship orbits along a circular path around the Earth, its period is 100 minutes. What is the area of the surface of the Earth which is seen by the astronaut at a certain instant? (Neglect the refraction of light due to the atmosphere.)
(4 pont)
solution (in Hungarian), statistics
P. 5102. A trolley of mass \(\displaystyle m_1\) is moving at a speed of \(\displaystyle v_0\) along the horizontal floor towards another trolley of mass \(\displaystyle m_2\), which is at rest. On the top of each trolley there is a thin rectangular block of mass \(\displaystyle m\). The coefficient of static friction between the blocks and the surface of the trolleys is \(\displaystyle \mu_0\). There is a spring of spring constant \(\displaystyle D\) on the stationary trolley.
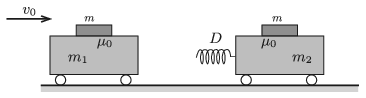
Will any of the blocks slide due to the collision?
Data: \(\displaystyle m_1=0.2~\rm kg\); \(\displaystyle m_2=m=0{.}1~\rm kg\); \(\displaystyle \mu_0=0.5\); \(\displaystyle D=12~\rm N/m\); \(\displaystyle v_0=1~\rm m/s\).
(4 pont)
solution (in Hungarian), statistics
P. 5103. A slinky of mass \(\displaystyle m\) is suspended at one of its ends, due to its own weight it is extended to a length of \(\displaystyle L\). Then one end of the slinky is held at a height of \(\displaystyle H\) above a horizontal tabletop \(\displaystyle (H<L)\), so the slinky is not extended totally. What are the forces which are exerted at the suspension and at the support? (The unstretched length of the slinky is negligible with respect to \(\displaystyle H\).)
(5 pont)
solution (in Hungarian), statistics
P. 5104. There is a sample of nitrogen gas in a container closed with a piston. The pressure of the gas is decreased by slowly pulling out the piston. What is the molar heat capacity of the gas in this process if 1% increase in the volume results in 0.5% change in the pressure?
(4 pont)
solution (in Hungarian), statistics
P. 5105. There are three metal spheres of radius \(\displaystyle R\) in vacuum. Their centres are collinear. The distance of the middle sphere from the other two spheres is \(\displaystyle d\gg R\). The temperature values of the two spheres at the sides are constant: one of them has temperature \(\displaystyle T_1\), and the other has \(\displaystyle T_2\). What is the steady-state temperature of the middle sphere if all the spheres can be considered black bodies?
(5 pont)
solution (in Hungarian), statistics
P. 5106. A thin light ray enters into a prism of refractive index \(\displaystyle n_1=1.8\). The cross section of the prism is an equilateral triangle and the path of the light ray in the prism is symmetrical about the bisecting plane.
\(\displaystyle a)\) What is the angle of incidence of the incident light ray?
\(\displaystyle b)\) What is the angle between the incident ray and the light ray which emerges from the prism, the so-called angle of deviation?
\(\displaystyle c)\) Then the light source and prism system is fixed and submerged into some liquid of refractive index of \(\displaystyle n_2=1.5\). What is the angle of deviation of the light ray in this case?
(5 pont)
solution (in Hungarian), statistics
P. 5107. A tetrahedron-shaped circuit is soldered from six resistors. Five of the resistors are alike and have the same resistance value whilst the sixth one is different. Only one ohm-meter is available, and the circuit, which seemingly contains six alike resistors cannot be taken apart. At most how many measurements are needed to find the resistor which has different resistance value, and also to find the resistance value of each resistor? If we are lucky, how many measurements are needed to find the resistance values?
(5 pont)
solution (in Hungarian), statistics
P. 5108. At least what speed should a small object of mass \(\displaystyle m\) and of charge \(\displaystyle q\) be projected upward in vacuum in order that it reaches another object of charge \(\displaystyle Q\), (vertically) above it at a height of \(\displaystyle \ell\)? (\(\displaystyle Q\) and \(\displaystyle q\) are opposite charges.)
Data: \(\displaystyle m=10^{-5}\) kg, \(\displaystyle q=4.0\cdot10^{-9}\) C, \(\displaystyle Q= - 1.0\cdot10^{-7}\) C, \(\displaystyle \ell=0.36\) m.
(5 pont)
solution (in Hungarian), statistics
P. 5109. What is the wavelength of an electron if its kinetic energy is
\(\displaystyle a)\) \(\displaystyle 1.75\cdot 10^{-16}\) J;
\(\displaystyle b)\) 20 GeV?
(5 pont)
solution (in Hungarian), statistics
P. 5110. The lengths of the semi-major axis of two satellites orbiting around the Earth are the same. The ratio of the speeds of the two satellites when they are at perigee (the point at which the satellite is the closest to the Earth) is \(\displaystyle \tfrac32\), and the eccentricity of the orbit of that satellite which is faster at this point is 0.5.
Determine the ratio of the speeds of the satellites when they are at apogee (at the furthest point from the Earth), and the eccentricity of the path of the other satellite.
(6 pont)
Upload your solutions above.
