KöMaL Problems in Physics, May 2019
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'M'Deadline expired on June 11, 2019. |
M. 387. Cut an approximately spherical orange into two parts and place one of the two ``hemispheres'' on a slope, with the curved part of the orange touching the surface of the slope. Use a slope whose angle of elevation can easily be changed, and the surface of which is rough enough so the orange does not slip on it. Increase the angle of elevation of the slope, until the orange stays at rest in a slant position. Take a picture of the orange on the slope. Measure the maximum angle of elevation of the slope, and construct the centre of mass of the hemisphere.
(6 pont)
 |
Problems with sign 'G'Deadline expired on June 11, 2019. |
G. 673. A cuboid-shaped aquarium is slowly filled with water. By what factor the force exerted on a wall of the cuboid is greater when the aquarium is fully filled with water than when the aquarium is filled only to one third of its height?
(3 pont)
solution (in Hungarian), statistics
G. 674. Between Budapest and Veresegyház there are two types of trains: passenger trains and fast passenger trains. Determine the average speeds of both types of trains using a railway timetable available on the internet (for example elvira.mav-start.hu). How will the average speeds of the trains change if the train has to wait ten minutes for another train coming from the opposite direction?
(3 pont)
solution (in Hungarian), statistics
G. 675. A plane mirror is placed horizontally on a horizontal floor, and above it another plane mirror, facing towards the first one is placed as well. There is a small black spot in the middle of the top mirror. The mirror at the top is released and begins to fall at an acceleration of \(\displaystyle g\). What are the magnitudes and the directions of the acceleration of the images of the spot?
(4 pont)
solution (in Hungarian), statistics
G. 676. At dawn on 21 January 2019 there was a total eclipse of the Moon, which could be seen from Hungary, and was observable for more than an hour. What factors does the length of the total eclipse of the Moon depend on?
(4 pont)
 |
Problems with sign 'P'Deadline expired on June 11, 2019. |
P. 5132. We set off on a journey by car. The meter, which shows the average speed of the car from the start of the journey, reads 37 km/h when we reach the motorway. From that time onward, we travel at the greatest allowed speed (130 km/h).
\(\displaystyle a)\) Determine how the average speed of the car changes as a function of time. What circumstances affect this function?
\(\displaystyle b)\) How much time elapses until the value of the average speed – rounded to the nearest integer – is going to be 130 km/h?
(4 pont)
solution (in Hungarian), statistics
P. 5133. Objects of mass \(\displaystyle m\) are attached to the ends of a thread wound through a standing pulley. Below one of the objects another object of mass \(\displaystyle m_1\) is hung by means of a thread of length \(\displaystyle \ell\), so the object of mass \(\displaystyle m_1\) will be at a height of \(\displaystyle h\), measured from the ground. After releasing the system, how much time elapses between the instants when the two objects hit the ground?
Data: \(\displaystyle m=2\) kg, \(\displaystyle m_1=1\) kg, \(\displaystyle \ell=2\) m, \(\displaystyle h=3\) m.
(3 pont)
solution (in Hungarian), statistics
P. 5134. One end of a very thin negligible-mass rod of length \(\displaystyle R=0{.}64~\rm m\) is attached to a horizontal axle, whilst to its other end a small sphere of mass \(\displaystyle m=5\) g and of charge \(\displaystyle Q=6\cdot10^{-7}\) C is fixed. The whole structure is placed into vertically downward uniform electric field of strength \(\displaystyle E=2\cdot10^5\) V/m. The rod is put into the horizontal position shown in the figure.
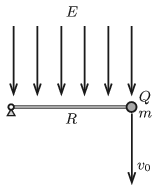
\(\displaystyle a)\) What vertically downward initial speed \(\displaystyle v_0\) should the small sphere be given in order that after 3/4 of a complete revolution the rod gets stuck, and at the same time the small sphere is ceased to be fixed to the rod, and flies back exactly to its initial position?
\(\displaystyle b)\) What is the angle between the velocity of the small sphere and the horizontal, when the sphere passes its initial position?
\(\displaystyle c)\) What is the ratio of the speed of the sphere when it passes its initial position to that of its initial value?
(5 pont)
solution (in Hungarian), statistics
P. 5135. The centre of mass of the driver of weight \(\displaystyle G=840\) N, when he is sitting in the car, is at point \(\displaystyle A\) as shown in the figure. (The scale figure on the right shows the top view of the car. Point \(\displaystyle A\) is the first left trisecting point of the rectangle determined by the wheels of the car.)
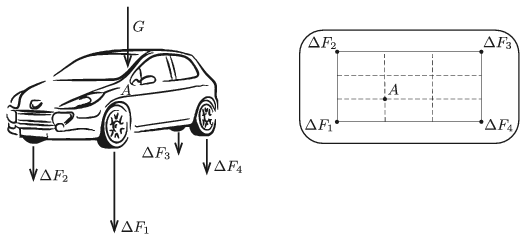
By what amount are the magnitudes of the forces exerted on the wheels of the car increased when the driver is sitting in the car compared to the case when he is not in the car? The springs at the wheels are alike and they all obey Hooke's law.
(5 pont)
solution (in Hungarian), statistics
P. 5136. Both ends of a thread are attached to the top two vertices of a rectangular picture of sides \(\displaystyle A\) and \(\displaystyle B\), and then the picture is hung to a peg. What should the least length of the thread be in order that the picture remain in a stable symmetric position? Friction between the peg and the thread is negligible, and the centre of mass of the picture coincides with the geometric centre of the rectangle.
(5 pont)
solution (in Hungarian), statistics
P. 5137. The gasbag of an airship of volume \(\displaystyle 31\,900\) m\(\displaystyle {}^3\) is filled with hydrogen and is staying at rest in air. The values of the temperature and the pressure of the ambient dry air are the same as those of the hydrogen in the gasbag: the temperature is \(\displaystyle 20\;{}^\circ\)C and the pressure is 95.3 kPa.
\(\displaystyle a)\) Calculate the buoyant force of the air.
\(\displaystyle b)\) What would the value of the buoyant force be if the ambient air had 70% relative humidity, at the same pressure and at the same temperature?
(4 pont)
solution (in Hungarian), statistics
P. 5138. The cooling of water is investigated in alike containers of negligible heat capacity. In each case the initial temperature of the sample of water is \(\displaystyle 80\;{}^\circ\)C, and the aimed final temperature is \(\displaystyle 40\;{}^\circ\)C. The temperature of the environment is \(\displaystyle 30\;{}^\circ\)C, which does not change during the measurements.
\(\displaystyle (i)\) Firstly it was measured that 2 litres of water cooled from \(\displaystyle 80\;{}^\circ\)C to \(\displaystyle 40\;{}^\circ\)C in a time of \(\displaystyle t_0\).
\(\displaystyle (ii)\) Secondly, we waited only until the 2 litres of water initially having a temperature of \(\displaystyle 80\;{}^\circ\)C cooled to a temperature of \(\displaystyle 50\;{}^\circ\)C (which took a time of \(\displaystyle t_1\)). Then 1 litre of water was quickly poured out and was replaced with 1 litre of water at a temperature of \(\displaystyle 30\;{}^\circ\)C.
\(\displaystyle (iii)\) Then the measurement was repeated such that 1 litre of the initial 2 litres of water at a temperature of \(\displaystyle 80\;{}^\circ\)C was poured out and immediately replaced by 1 litre water at a temperature of \(\displaystyle 30\;{}^\circ\)C. The mixture reached the temperature of \(\displaystyle 40\;{}^\circ\)C in a time of \(\displaystyle t_2\).
\(\displaystyle (iv)\) Finally the 2 litres water of initial temperature \(\displaystyle 80\;{}^\circ\)C, was left to cool to \(\displaystyle 60\;{}^\circ\)C, and then quickly 1 litre of water was poured out and replaced by 1 litre of water of temperature \(\displaystyle 30\;{}^\circ\)C, and then the mixture was left to cool to a temperature of \(\displaystyle 40\;{}^\circ\)C. The total time of cooling in this case was \(\displaystyle t_3\).
Which is the quickest and which is the slowest way of cooling? Express the times of \(\displaystyle t_1\), \(\displaystyle t_2\) and \(\displaystyle t_3\) in terms of \(\displaystyle t_0\). It can be assumed that the rate of cooling of an object is proportional to the temperature difference between the object and the environment, that is Newton's law of cooling can be applied.
(5 pont)
solution (in Hungarian), statistics
P. 5139. A monochromatic light beam enters into a glass prism of vertex angle \(\displaystyle 75^\circ\). The prism is in water, and the angle of incidence of the light beam is \(\displaystyle 45^\circ\). The light beam emerges from the glass after two refractions. \(\displaystyle a)\) How and by what percent does the wavelength of the light change when the light emerges from the glass and enters into the water? \(\displaystyle b)\) By what angle does the direction of the light beam which emerges from the glass after the two refractions change with respect to that of the incident ray? \(\displaystyle c)\) At what angle of incidence would the light beam not emerge from the prism at the second boundary? The refractive index of glass is \(\displaystyle \frac32\), and that of the water is \(\displaystyle \frac43\).
(4 pont)
solution (in Hungarian), statistics
P. 5140. Newton's rings are created by a plano-convex lens placed to a plan-parallel glass sheet illuminated by light of wavelength 0.6 \(\displaystyle \mu\)m. The refractive index of glass is 1.5, the focal length of the lens is 2.7 m.
\(\displaystyle a)\) What is the radius of the fourth bright ring?
\(\displaystyle b)\) How will the (dark and bright) ring pattern change if the lens is moved a bit further from the plan-parallel glass sheet?
(5 pont)
solution (in Hungarian), statistics
P. 5141. The plates of a parallel-plate condenser shown in the figure are horizontal and they are at a distance of \(\displaystyle d_0=4\) cm from each other. The condenser is in vacuum. An aluminium sheet of width \(\displaystyle d_0/4\) is placed on the lower plate, and high voltage is connected to the condenser.
\(\displaystyle a)\) What should the value of \(\displaystyle U_0\) be in order that the sheet rise?
\(\displaystyle b)\) At a given applied voltage of \(\displaystyle U\) what is the width of the aluminium sheet that can rise from the lower plate of the condenser of plate distance \(\displaystyle d_0\)?
\(\displaystyle c)\) Is there a voltage value at which the sheet surely rises, independently of the width of the sheet (provided that it is less than \(\displaystyle d_0\))?
(Assume that the aluminium sheet remains horizontal all the time. The sides of the condenser plates are much greater than \(\displaystyle d_0\), and wind effects are negligible.)
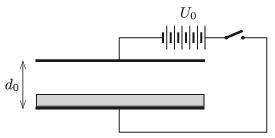
(5 pont)
solution (in Hungarian), statistics
P. 5142. A spacecraft of mass \(\displaystyle M\) revolves around the Sun along a circular path of radius \(\displaystyle r\), at a constant speed of \(\displaystyle v_0\). Its motion is affected only by the gravity of the Sun. Scientists on Earth intend to launch an absolutely black and perfectly spherical probe from the spacecraft. The radius of the probe is \(\displaystyle R\), its mass is \(\displaystyle m\), and it is made of some unknown material of density \(\displaystyle \varrho\). The sphere is intended to be put to a circular trajectory of radius \(\displaystyle r\) (same as for the mother spacecraft) around the Sun. Assume that the sphere conducts heat sufficiently well so that it is able to maintain uniform temperature (which we denote by \(\displaystyle T\)) and that this temperature stabilises at \(\displaystyle T = 180\) K after the launch. Assume that the Sun is a black body of temperature \(\displaystyle T_\odot = 5778\) K, its mass is \(\displaystyle M_\odot = 1.99\cdot 10^{30}\) kg, and its radius is \(\displaystyle R_\odot = 6.96 \cdot 10^8\) m. The value of the solar luminosity to be used throughout this question is \(\displaystyle L_\odot = 3.83\cdot 10^{26}\) W.
\(\displaystyle a)\) Find the value of \(\displaystyle r\) in astronomical units (\(\displaystyle 1~\mathrm{AU} = 1.496 \cdot 10^8\) km).
\(\displaystyle b)\) Using the conservation of linear momentum for photons incident on the sphere, find the magnitude of the force \(\displaystyle F_r\), which is the force exerted on the sphere by the radiation. Write your answer in terms of \(\displaystyle r\), \(\displaystyle R\), \(\displaystyle L_\odot\) and \(\displaystyle c\), where \(\displaystyle c\) is the speed of light in vacuum. The momentum \(\displaystyle p\) of a single photon with energy \(\displaystyle E\) can be expressed as \(\displaystyle p = E/c\).
\(\displaystyle c)\) Find the speed of the sphere \(\displaystyle v'\) when the radius of its orbit is \(\displaystyle r\). Write your answer in terms of \(\displaystyle r\), \(\displaystyle R\), \(\displaystyle L_\odot\), \(\displaystyle \varrho\), \(\displaystyle v_0\) and \(\displaystyle c\). You should assume that the motion of the sphere is affected only by the gravity of the Sun and the radiation pressure discussed in question \(\displaystyle b)\). Notice that in order to maintain the sphere's circular orbit at radius \(\displaystyle r\), we have to slow it down a little. This can be achieved be launching it opposite to the direction of spacecraft's motion at a speed \(\displaystyle \Delta v\) relative to the spacecraft. Also, in order to avoid dangerous destabilisation of the spacecraft's motion, the maximum admissible impulse the spacecraft can impart on the sphere is \(\displaystyle \Delta p_\text{max} = 1~\mathrm{kg\;m\;s^{-1}}\).
\(\displaystyle d)\) Find (numerically) the maximum radius \(\displaystyle R_\text{max}\) of the sphere, at which any dangerous destabilisations of the spacecraft during the launch can be avoided. Assume that \(\displaystyle m \ll M\) and \(\displaystyle \Delta v = v_0 - v' \ll v_0\). Use the approximation \(\displaystyle \sqrt{1 - x} \approx 1 - x/2\), if \(\displaystyle |x| \ll 1\). For the missing data give reasonable estimations.
(6 pont)
Upload your solutions above.
