KöMaL Problems in Mathematics, October 2005
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on November 10, 2005. |
K. 49. 15 teams participated in a football tournament. Every team played each of the other teams once. 3 points were awarded for winning, 2 for a draw and 1 point for losing the game. At the end of the tournament, every team had a different number of points, 21 being the lowest score. Prove that the team with the highest score has played at least one draw.
Suggested by B. Szalkai, Veszprém
(6 pont)
solution (in Hungarian), statistics
K. 50. In the quadrilateral ABCD, AB=AC=DB, and the diagonals are perpendicular. Find the sum of the angles ACB and ADB.
(6 pont)
solution (in Hungarian), statistics
K. 51. How many number sets of at least two elements are there, such that the elements are consecutive positive integers and their sum is 100?
(6 pont)
solution (in Hungarian), statistics
K. 52. The Figure shows the planned footpaths for a park in a city. What is the total length of the paths to be constructed if the lengths of the two kinds of segments marked in the diagram are 60 metres and 30 metres, respectively?
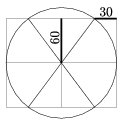
(6 pont)
solution (in Hungarian), statistics
K. 53. How many six-digit numbers of the form ababab can be obtained by multiplying six different primes?
(6 pont)
solution (in Hungarian), statistics
K. 54. A printing press is working on a board game that uses two kinds of figures moving on the board: dogs and cats. The dog and cat figures are to be cut out of cardboard. The cat to dog ratio in the set of figures packed in the box with each game is 5:3. To reduce wastes, the figures are printed on large sheets of cardboard in two different arrangements. One type of sheet contains 28 dogs and 28 cats, and the other one contains 42 cats. In what proportion should the two types of sheets printed in order to obtain them in the right proportion after cutting out?
(6 pont)
 |
Problems with sign 'C'Deadline expired on November 15, 2005. |
C. 820. Let 0 a,b,c,d
a,b,c,d 2005 be whole numbers. What is the probability that the number ab+cd is even?
2005 be whole numbers. What is the probability that the number ab+cd is even?
(5 pont)
solution (in Hungarian), statistics
C. 821. A unit square ABCD is rotated about its vertex C through 90o. Determine the area swept out by the side AB.
(5 pont)
solution (in Hungarian), statistics
C. 822. Let x and y denote non-negative real numbers. Prove that .
(5 pont)
solution (in Hungarian), statistics
C. 823. On its second birthday, a department store introduced sales prices. Those buying merchandise for more than 50 000 forints (HUF) enjoyed two successive discounts. Both percentage reductions were whole numbers less than 10. A television set that originally cost 69 000 forints was sold for 60 306 forints. Calculate the percentages.
(5 pont)
solution (in Hungarian), statistics
C. 824. Consider the truncated cone determined by the circumscribed circle of the base of a cube, and the inscribed circle of the top face of the cube. Find the ratio of the volume of the truncated cone to that of the cube.
(5 pont)
 |
Problems with sign 'B'Deadline expired on November 15, 2005. |
B. 3842. Given are five 15-litre vessels, containing 1, 2, 3, 4, and 5 litres of water, respectively. We are allowed to double the amount of water in any chosen vessel from another one. What is the largest possible amount of water that can be collected in a vessel by repeating this step?
(3 pont)
solution (in Hungarian), statistics
B. 3843. Is it possible to select four distinct points on the plane, such that through every pair of points there is a circle that has equal tangents from the other two points?
(3 pont)
solution (in Hungarian), statistics
B. 3844. The legs of a right-angled triangle are a and b, its hypotenuse is c. The radius of the escribed circle drawn to the leg b (i.e. the one touching that leg on the outside and also touching the extensions of the other two sides) is 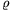 b. Prove that b+c=a+2
b. Prove that b+c=a+2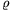 b.
b.
(3 pont)
solution (in Hungarian), statistics
B. 3845. Construct the triangle with ruler and compass ABC, given the lengths of the sides AB and AC, and the distance of the vertex A from the point that divides the side BC in the ratio 2:1.
(4 pont)
solution (in Hungarian), statistics
B. 3846. Solve the equation .
(4 pont)
solution (in Hungarian), statistics
B. 3847. Given an angle and a point in its interior, construct the line through the point that encloses a triangle of minimum area with the arms of the angle.
(5 pont)
solution (in Hungarian), statistics
B. 3848. A convex 100-sided polygon K lies in the interior of a square whose side is 1 metre. Show that it is possible to select three vertices of K, such that they form a triangle of smaller area than 8 cm2.
(5 pont)
solution (in Hungarian), statistics
B. 3849. A fair coin is tossed until both outcomes, i.e. heads and tails are obtained at least once. What is the expected value of the number of tosses needed?
(5 pont)
solution (in Hungarian), statistics
B. 3850. Consider the areas and perimeters of the rectangular sections of a regular tetrahedron of unit edge. In what intervals do they vary?
(4 pont)
solution (in Hungarian), statistics
B. 3851. Consider the functions obtained as compositions of the functions ,
, each used a finite number of times; for example
. Is it possible to obtain the function x
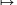 x+1 in this way? (It is allowed to cancel finitely many numbers from its domain.)
x+1 in this way? (It is allowed to cancel finitely many numbers from its domain.)
(5 pont)
 |
Problems with sign 'A'Deadline expired on November 15, 2005. |
A. 380. The convex n-sided polygon K lies in the interior of a unit square. Show that it is possible to select three vertices of the polygon that form a triangle of smaller area than units.
(5 pont)
A. 381. A die of n faces is rolled until each of the n possible outcomes is obtained at least once. What is the expected value of the number of rolls needed?
(5 pont)
A. 382. S and T are disjoint sets, * is a binary operation on the elements of S and o is a binary operation on the elements of T. (That is, if a,b S and c,d
S and c,d T, then a*b
T, then a*b S and cod
S and cod T). Each operation is associative. In other words, (S,*) and (T,o) are semigroups. It is also given that for every t
T). Each operation is associative. In other words, (S,*) and (T,o) are semigroups. It is also given that for every t T there are elements u,v
T there are elements u,v T, such that uot=tov=t. Let
T, such that uot=tov=t. Let denote an arbitrary mapping. Define the operation
on the set S
 T as follows:
T as follows:
Show that the operation is associative if and only if f is a homomorphism, that is, f(a*b)=f(a)of(b) for all a,b
 S.
S.
Czech competition problem
(5 pont)
Upload your solutions above.
