KöMaL Problems in Mathematics, March 2010
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on April 12, 2010. |
K. 247. During the first three years of her life, Sleeping Beauty slept an average of 14 hours a day. Then, until she was 16 years old she slept 8 hours a day, and then from her 16th birthday onwards, when she wounded her finger with the reel, she slept 24 hours a day for 100 years. A filbert mouse hibernates for 5 months of the year (from 1 November to 31 March), and in the rest of the year it spends a daily average of 8 hours awake (during the nighttime hours). After how many years of sleep should the prince have woken up Sleeping Beauty so that her daily average of sleep from her birth to her waking up equals that of a filbert mouse? (For simplicity, ignore leap years, that is, assume that February is always 28 days long.)
(6 pont)
solution (in Hungarian), statistics
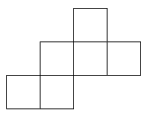
K. 248. The diagram shows a net of a cube. In how many different ways is it possible to colour two of the six squares red, and the other four with four different colours: white, green, yellow and blue, so that the resulting cube does not have two adjacent faces of the same colour?
(6 pont)
solution (in Hungarian), statistics
K. 249. 5, 10, 20, 50, 100 and 200-forint coins (HUF, Hungarian currency) are collected in a huge piggy bank. At the moment, there are 18 200 forints in it. Before the last coin was added, the number of various types of coins was inversely proportional to the value of the coins. How many 200-forint coins are there in the piggy bank now?
(6 pont)
solution (in Hungarian), statistics
K. 250. Two people tried to estimate the size of the audience at an open air concert. One of them guessed there were 2700 spectators, the other one guessed 3600. It turned out that one of the percentage errors made was twice the other, but one underestimated and the other overestimated the audience. What may have been the number of spectators at the concert?
(6 pont)
solution (in Hungarian), statistics
K. 251. Extend each diagonal of a square of side in one direction by the length of the side.
a) How long is the line segment connecting the new endpoints of the extensions?
b) Show that there is a vertex of the square that forms an isosceles triangle with the new endpoints of the extensions.
(6 pont)
solution (in Hungarian), statistics
K. 252. The sum of six consecutive integers is multiplied by the sum of the next six integers. Prove that the product obtained in this way will always leave the same remainder when divided by 36.
(6 pont)
 |
Problems with sign 'C'Deadline expired on April 12, 2010. |
C. 1025. For integers a and b, let aob denote the number one greater than the non-smaller one of the two numbers, and let a*b denote the number one greater than the non-greater one of the two numbers. Solve the equation (xo2010)*2011=x+2.
(5 pont)
solution (in Hungarian), statistics
C. 1026. Extend each diagonal of a square in one direction by a length equal to the side of the square. How many isosceles triangles are determined by the endpoints of the extensions and the vertices of the square?
(5 pont)
solution (in Hungarian), statistics
C. 1027. Solve the equation (ax2+bx+14)2+(bx2+ax+8)2=0 on the set of integers. a and b are integers.
(5 pont)
solution (in Hungarian), statistics
C. 1028. ABC is an equilateral triangle in the plane. Consider the plane figure formed by the points for which the distance from vertex A is not greater than the side of the triangle and the distances from vertices B and C are not smaller than the side of the triangle. By what factor is the area of the figure greater than the area of the triangle?
(5 pont)
solution (in Hungarian), statistics
C. 1029. In a gift shop, there are 160 Easter greating cards stacked on the counter. A customer separates the stack of cards in two (not necessarily equal) parts, each containing at least two cards. He buys one card of one of the two stacks. The next customer follows the same procedure: he divides one of the stacks in two (according to the above conditions), buys one card from one part. Then comes the next customer, and so on. Is it possible in this way to obtain stacks of cards on the counter that consist of four cards each?
(5 pont)
 |
Problems with sign 'B'Deadline expired on April 12, 2010. |
B. 4252. For what integers n>2 is it true that every convex polygon of n vertices has a side such that neither of the two angles lying on the side is acute?
(3 pont)
solution (in Hungarian), statistics
B. 4253. A 6×6×6 cube is built out of blue and red building blocks, such that every 2×2×2 part consists of exactly 3 red cubes and 5 blue cubes. Prove that it is also true for the big cube that exactly 3 vertices are red and 5 are blue.
(4 pont)
solution (in Hungarian), statistics
B. 4254. Is there a function defined on the points of the plane, which is not identically zero but the sum of its values at the vertices of every regular pentagon in the plane is zero?
(4 pont)
solution (in Hungarian), statistics
B. 4255. Prove that if 2n+1 and 3n+1 are square numbers for some positive integer n then 5n+3 cannot be a prime number.
(4 pont)
solution (in Hungarian), statistics
B. 4256. Is there a triangle in which an angle is divided into four equal parts by the altitude, median and angle bisector drawn from the vertex?
(4 pont)
solution (in Hungarian), statistics
B. 4257. A group of 11 000 astronauts are trained for a Mars mission. Given that from any 4 of them it is possible to select a suitable crew of 3 members for the landing module, prove that it is possible to select 5 astronauts such that any 3 of them form a suitable crew.
(Kvant)
(5 pont)
solution (in Hungarian), statistics
B. 4258. Given the triangle ABC and the line e, determine the point P of e for which PA2+2PB2+3PC2 is a minimum.
(3 pont)
solution (in Hungarian), statistics
B. 4259. A circle passes through vertices B and C of a triangle ABC. It intersects side AB at D and side AC at E. The median AF intersects DE at G. Prove that .
(4 pont)
solution (in Hungarian), statistics
B. 4260. Solve the simultaneous equations ,
.
(4 pont)
solution (in Hungarian), statistics
B. 4261. A house has the shape of a cube. A roof is built on it that consists of two isosceles triangles and two symmetrical trapeziums. The edges of the roof are all equal, and the angles enclosed by adjacent faces are all equal. Find the ratio of the edge of the roof to the edge of the cube.
(5 pont)
 |
Problems with sign 'A'Deadline expired on April 12, 2010. |
A. 503. In space, there are given some vectors u1,u2,...,un and v such that |u1| 1, ..., |un|
1, ..., |un| 1 and |v|
1 and |v| 1, and u1+...+un=0. Show that
1, and u1+...+un=0. Show that
|u1-v|+...+|un-v| n.
n.
(5 pont)
A. 504. Prove that for arbitrary integers 0<r<k<t there exists a positive integer N(r,k,t) which satisfies the following property: whenever G is an r-uniform hypergraph with at least N(r,k,t) vertices such that there is at least one hyperedge on any k vertices, then G contains a complete subgraph with t vertices. (A hypergraph is a graph whose edges are arbitrary subsets of the vertices. The graph is called r-uniform if all edges contain exactly r vertices. An r-uniform hypergraph is complete if any r of its vertices form an edge.)
(5 pont)
A. 505. In a cyclic quadrilateral ABCD, the points O1 and O2 are the incenters of triangles ABC and ABD, respectively. The line O1O2 meets BC and AD at E and F, respectively.
(a) Show that there exists a circle k which touches the lines BC and AD at E and F, respectively.
(b) Prove that k also touches the circumcirlce of ABCD.
Proposed by: János Nagy, Budapest)
(5 pont)
Upload your solutions above.
