KöMaL Problems in Mathematics, November 2011
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on December 12, 2011. |
K. 307. The rectangle in the figure is dissected into squares. The area of square A is 196 cm2, that of square B is 16 cm2, and the area of square C is 81 cm2. What is the area of the rectangle?
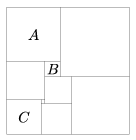
(6 pont)
solution (in Hungarian), statistics
K. 308. A certain brand of breakfast cereal is sold in three boxes of different sizes that also have different colours: red, green and blue. The red box is 50% more expensive than the blue box and weighs 20% less than the green box. The green box weighs 50% more than the blue box and costs 25% more than the red box. Which box has the lowest price per kilogram?
(6 pont)
solution (in Hungarian), statistics
K. 309. The plane is divided into four parts by two intersecting lines. The measures of the four angles in degrees are 5x-9, 4x+27, x+y-30, y-x+3z, not necessarily in this order. What may be the four angles?
(6 pont)
solution (in Hungarian), statistics
K. 310. We found a method for multiplying two numbers between 90 and 100: Add the two numbers, subtract 100 from the sum, and then write after the result the product of the differences of the original numbers from 100. E.g. in the case of 97 and 94, 97+94-100=91 and (100-97)(100-94)=18, so the product is 9118 and indeed, 97×94=9118. Why is this a correct method? How can it be extended so that it can be used for multiplying any two two-digit numbers?
(6 pont)
solution (in Hungarian), statistics
K. 311. The number 772009+772010+772011+772012 is evidently divisible by 7 and 11. Find all prime factors of the number.
(6 pont)
solution (in Hungarian), statistics
K. 312. The vertices of a trapezium ABCD lying in the first quadrant of the coordinate plane are A(a;0); B(8;b); C(3;b); D(0;0), where a and b are integers. Given that the area of the trapezium is 121, find the missing coordinates.
(6 pont)
 |
Problems with sign 'C'Deadline expired on December 12, 2011. |
C. 1095. Which product is greater: or
?
(5 pont)
solution (in Hungarian), statistics
C. 1096. The length of the edge of a cube is an integer. Consider one-third of the edge length, one half of the area of a face and one-sixth of the volume. Prove that the sum of the three numbers is an integer.
(5 pont)
solution (in Hungarian), statistics
C. 1097. A motorcycle has brand new tyres on both wheels. A tyre is considered worn if it has run 15 000 km on the rear wheel or 25 000 km on the front wheel. What is the maximum possible number of kilometres that the motorcycle can run until the tyres become worn if the front and rear tyres are interchanged at the appropriate time?
(5 pont)
solution (in Hungarian), statistics
C. 1098. Prove that if two opposite angles of a convex circumscribed quadrilateral are right angles then the quadrilateral is a kite.
(5 pont)
solution (in Hungarian), statistics
C. 1099. In a quadrilateral ABCD, M is the midpoint of line segment AB, and N is the midpoint of line segment CD. The length of diagonals AC and BD is , and they enclose an angle of 60o. Find the distance MN.
Suggested by G. Dávid, Matlap, Kolozsvár
(5 pont)
 |
Problems with sign 'B'Deadline expired on December 12, 2011. |
B. 4392. There are chessmen standing on a few fields of a 20×20 chessboard. A chessman can be removed from the board if at least one half of the fields in its row or column are vacant. What is the minimum number of chessmen needed for an appropriate arrangement such that no chessman can be removed from the board?
(3 pont)
solution (in Hungarian), statistics
B. 4393. Consider the vertices of a regular triangle, the centre of the triangle and all points that divide its sides in a 1:2 ratio. What is the largest number of points that can be selected out the points listed above, such that no three of them form a regular triangle? (Suggested by
A. Demeter, Matlap, Kolozsvár
(4 pont)
solution (in Hungarian), statistics
B. 4394. Consider the Fibonacci sequence defined by the recursive formula F1=F2=1, Fn=Fn-1+Fn-2. Prove that if k<m, then is a composite number.
Suggested by D. Lenger, Budapest
(4 pont)
solution (in Hungarian), statistics
B. 4395. Given a cyclic quadrilateral, construct a point in the interior of each side, such that they form a convex quadrilateral of the smallest possible perimeter.
(5 pont)
solution (in Hungarian), statistics
B. 4396. The inscribed circle of triangle ABC touches side b at F and side a at G. Prove that the foot of the perpendicular dropped from A onto the angle bisector of angle  lies on the line FG. (By conventional notation , side b lies opposite to vertex B and angle
lies on the line FG. (By conventional notation , side b lies opposite to vertex B and angle  is the angle at B, etc.)
is the angle at B, etc.)
(3 pont)
solution (in Hungarian), statistics
B. 4397. Prove that if n, k are positive integers then is divisible by n.
Suggested by D. Korándi, Budapest
(3 pont)
solution (in Hungarian), statistics
B. 4398. A1, B1 and C1 are given points on sides BC, CA and AB, respectively, of the acute-angled triangle ABC. Mark a point A2 on the circle AC1B1. Let B2 be the intersection (different from C1) of the line C1A2 with the circle BA1C1. Furthermore, let C2 be the intersection (different from A1) of the line A1B2 and the circle CB1A1. Prove that the points A2, B1 and C2 are collinear.
(4 pont)
solution (in Hungarian), statistics
B. 4399. A sack contains k red balls and n green balls. The balls are drawn out one by one, without replacement, until the first red ball is drawn. How many draws are needed on average?
Suggested by G. Maróti
(4 pont)
solution (in Hungarian), statistics
B. 4400. Is it possible to place a 1.05×1.05 square inside a unit cube?
(4 pont)
solution (in Hungarian), statistics
B. 4401. Let p=3n+1 be a prime number. Is it possible for the numbers to leave pairwise different remainders when divided by p?
(5 pont)
 |
Problems with sign 'A'Deadline expired on December 12, 2011. |
A. 545. Prove that whenever a>b>1 are integers such that a+b divides ab+1 and a-b divides ab-1 then .
(Kolmogorov Cup, 2009)
(5 pont)
A. 546. Show that
for every positive integer k.
(5 pont)
A. 547. A tetrahedron OA1A2A3 is given. For i=1,2,3 let Bi be a point in the interior of the edge OAi and let Ci be a point on the ray OAi, beyond Ai. Suppose that the polyhedron bounded by the six planes OAi+1Ai+2 and BiAi+1Ai+2 (i=1,2,3) circumscribes a sphere, and the polyhedron bounded by the planes BiAi+1Ai+2 and CiAi+1Ai+2 also circumscribes a sphere. Prove that the polyhedron bounded by the planes OAi+1Ai+2 and CiAi+1Ai+2 also circumscribes a sphere.
(5 pont)
Upload your solutions above.
