KöMaL Problems in Physics, November 2012
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'M'Deadline expired on December 10, 2012. |
M. 327. Measure the speed of a descending balloon, which is filled with air, as a function of the diameter of the balloon. (Do not change the balloon, just alter the amount of air in it.)
(6 pont)
 |
Problems with sign 'P'Deadline expired on December 10, 2012. |
P. 4475. During the siege of the fortress of Eger the defenders used cannons to shoot the Turkish troops surrounding the fortress. Once the cannonball reached the top of its path 2 seconds after its projection, and during 3 further seconds its speed became 50 m/s. Estimate the initial speed and the direction of the projection of the cannonball.
(3 pont)
solution (in Hungarian), statistics
P. 4476. Kate invited her friends to her birthday party. She wanted to endear herself to her friends by making them some ice-cream. She mixed the ice-cream powder with water at 4 o'clock in the afternoon, her friends were invited to come to 6 o'clock, and she was a bit worrying whether the ice-cream will be ready or not. In order not to worry so much, she measured how fast the initially 25 oC ice-cream mixture cools down in the freezer. She observed that after 10 minutes the temperature of the ice-cream was 21 oC. Was she able to serve the ice-cream to her friends in the party if the party lasted until 10 at night, and the ice-cream must cool down to at least -6 oC? (Suppose that the heat extraction of the freezer is uniform, and the thermal properties of the liquid ice-cream and the ice-cream are the same as those of the water and ice.)
(4 pont)
solution (in Hungarian), statistics
P. 4477. A small incandescent lamp, rated at 2 W/20 V, is to be operated with the aid of a 100-ohm variable resistor and a voltage supply of voltage 40 V. How can this be done?
(4 pont)
solution (in Hungarian), statistics
P. 4478. A cyclist is riding his bicycle all out while he goes uphill at a speed of v1=12 km/h, and he can go downhill, on the same slope, at a speed of v2=36 km/h. What is his top speed on the level road, if his maximum strength to ride the bike is independent of the speed of the bicycle?
(5 pont)
solution (in Hungarian), statistics
P. 4479. An easily moveable, insulated piston, of cross section A=2 dm2 and of mass m=5 kg, confines some air in a vertical thermally insulated cylinder. The air is heated by a heating element of power 200 W.
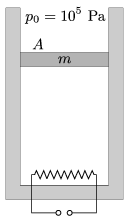
a) What is the speed of the piston?
b) By what amount does the internal energy of the air change in 2 s?
(5 pont)
solution (in Hungarian), statistics
P. 4480. In a long straight coaxial cable the centre conductor has a radius of r1, and the outer metallic shield has an inner radius of r2, and an outer radius of r3. (Between the two conductors there is a dielectric insulator.) In the two conductors the current of I flows in the opposite direction. Determine the magnetic induction vector B around the cable as a function of the distance r measured from the symmetry axis of the cable.
(4 pont)
solution (in Hungarian), statistics
P. 4481. A big piece of positively charged metal sheet is illuminated by light of wavelength 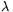 . The surface charge density of the metal is
. The surface charge density of the metal is  , and the work function of the metal is W.
, and the work function of the metal is W.
a) At what greatest distance from the metal can electrons be found?
b) At what speed do the electrons moving back to the sheet hit the sheet?
(Data:  =2.10-6 C/m2, W=0.41 aJ,
=2.10-6 C/m2, W=0.41 aJ, 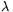 =400 nm.)
=400 nm.)
(4 pont)
solution (in Hungarian), statistics
P. 4482. Why are the dark lines in an absorption spectrum not exactly black?
(4 pont)
solution (in Hungarian), statistics
P. 4483. If it was possible to create a vacuum tube along the magnetic equator of the Earth, the protons and electrons in this tube would - theoretically - orbit along circular path, due to the magnetic field of the Earth.
a) Estimate the speed and the direction of their motion.
b) What would the energy of these particles be in eV?
c) Can particle beams having the above calculated energy be created nowadays?
d) How much would the light, which travels along the same ``circle'' due to appropriately placed mirrors, overtake the particles travelling in the tube in one circle?
(5 pont)
solution (in Hungarian), statistics
P. 4484. Estimate the pressure on the wall of a small cube of edge d, due to a neutron confined in the cube.
(5 pont)
solution (in Hungarian), statistics
P. 4485. Two alike balls are suspended next to each other and can swing in the plane of the figure on threads of length  . One ball is displaced by a distance of d and then released (d
. One ball is displaced by a distance of d and then released (d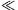
 ). The balls collide inelastically, their velocities decrease by a factor of k at each collision, with respect to the system of their centre of mass (0<k<1 is the collision number).
). The balls collide inelastically, their velocities decrease by a factor of k at each collision, with respect to the system of their centre of mass (0<k<1 is the collision number).
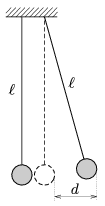
How will the balls move? What will the amplitude of the swings be after many collisions?
(6 pont)
Upload your solutions above.
