Mikor keletkezik ,,jó'' csillag?

Októberi számunk I. 59.-es informatika feladatában n-ágú szabályos csillagokat kellett rajzolni, mégpedig az összes lehetségeset. Ezeket úgy kapjuk, hogy a szabályos n-szög (n\(\displaystyle \ge\)5) egyik csúcspontjából indulva minden k-adikat összekötjük, amíg vissza nem érünk a kiindulási pontba (1. ábra). Csak azok az elfogadható megoldások, ahol valóban csillag keletkezik.

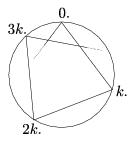
1. ábra

Definíció [1]. A szabályos csillagsokszöget a sík véges sok szakasza alkotja, ha minden végpontjuk két szakasz közös végpontja, és található hozzájuk olyan egybevágóság, amely a szakaszok egyikét egy tetszőlegesen előírt másikra fekteti, s amely a teljes alakzat helyét nem változtatja meg. A szabályos sokszögvonal is ilyen alakzat, de ezt nem nevezzük szabályos csillagsokszögnek. Egy szabályos sokszögnek a középponttól egyenlő (0-tól különböző) távolságra levő átlói szabályos csillagsokszöget alkotnak.

Tekintsük azt a szabályos csillagot, amelyet úgy kapunk, hogy a szabályos ötszögre alkalmazzuk a definíció második részét (2a. ábra).

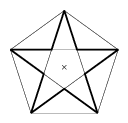
2a. ábra

Erre a csillagötszögre valóban igaz, hogy bármely két szakaszához található egybevágóság: vagy forgatással, vagy tengelyes tükrözéssel egymásra fektethetők (2b. ábra). A csillagötszög elnevezés megtévesztő, a 2. ábrák csillagának nyilván tíz oldala van.

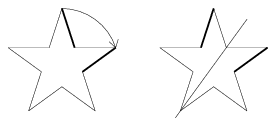
2b. ábra

Milyen további tulajdonságai vannak ezeknek az alakzatoknak? A szabályos csillag-n-szögnek 2n oldala van, a szimmetriák miatt az oldalak egyenlő hosszúak; szögei (amelyekből ugyancsak 2n van) közül minden második, n darab egyenlő nagyságú (ez legyen \(\displaystyle \alpha\)), a további, az előzőekkel szomszédos n darab szög ugyancsak egyenlő. A sokszögek szögösszegéből könnyen adódik, hogy

\(\displaystyle \alpha+\beta=360^\circ-\frac{360^\circ}{n}. \)

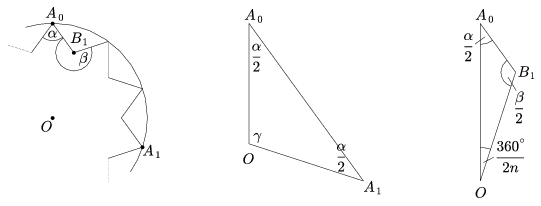
3a. ábra

Legyen ugyanis a megfelelő szabályos sokszög kiindulási csúcsa A₀, a k-adik csúcs A₁, a csillagsokszög A₀-lal (az óramutató járása szerint) szomszédos csúcsa pedig B₁. Az A₀A₁O háromszögben (3a. ábra) \(\displaystyle \gamma=\frac{k}{n}\cdot360^\circ\) (hiszen a szabályos n-szög első és k-adik csúcsáról van szó), tehát

Az A₀B₁O háromszögben:

amiből látszik, hogy valóban \(\displaystyle \frac{\alpha}{2}+\frac{\beta}{2}= 180^\circ-\frac{180^\circ}{n}\), tehát \(\displaystyle \alpha+\beta=360^\circ- \frac{360^\circ}{n}\), amely összeg k-tól független. (1)-ből és (2)-ből kiszámítható \(\displaystyle \beta\) értéke is:

\(\displaystyle \beta=180^\circ+(k-1)\frac{360^\circ}{n}. \)

A forgásszimmetria miatt a csillagsokszög másodszomszédos csúcsai egy-egy körön helyezkednek el: a k₁ és egy, az előzővel koncentrikus k₂ körön (3b. ábra).

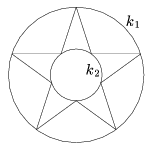
3b. ábra

Úgy tűnik, a csillagsokszög minden második szöge konkáv. Igaz-e ez? Ha a belső, k₂ kör sugarát növeljük (vagy csökkentjük), egy olyan alakzatot kapunk, amely megfelel a definíciónak, tehát ugyancsak nevezhetjük szabályos csillagsokszögnek. Erre általában nem igaz, hogy oldalai a szabályos sokszög átlóira illeszkednek. A ,,belső'' pontok mozgatását egészen addig folytathatjuk, amíg már nem lesznek konkáv szögeink, de még nem érik el a k₁ kört (ekkor szabályos 2n-szög keletkezik). Ezt megtehetjük, hiszen

\(\displaystyle \alpha+\beta=360^\circ-\frac{360^\circ}{n}<360^\circ\) (4a. ábra).

A definíció szerint ez is szabályos csillagsokszög, de ha a szabályos sokszöget nem tekintjük annak, előírhatjuk, hogy csillagsokszögünk minden második szöge legyen konkáv. Van egy átmeneti állapot, amikor \(\displaystyle \beta\)=180^o, ekkor a csillagsokszög n oldalú szabályos sokszöggé alakul át.

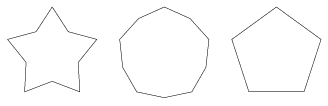
4a. ábra

Ha a belső, k₂ körre eső csúcsokat elforgatjuk a középpont körül, a forgásszimmetria továbbra is teljesül minden második oldalra, de a szomszédos oldalakra a tükörszimmetria már nem, tehát a keletkezett ,,körfűrész'' nem szabályos csillagsokszög (4b. ábra).

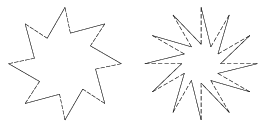
4b. ábra

Nézzük meg most már, hogy melyek az informatika feladat jó megoldásai, ha a szabályos n-szög k-szomszédos csúcsait kötjük össze. Így egy folytonos, zárt poligont (töröttvonalat) kapunk, amelynek bizonyos szakaszai metszik egymást, így ezt hurkolt poligonnak [1] nevezzük (csak ekkor beszélhetünk a feladat megoldásának tekintett szabályos csillagról).

Ha \(\displaystyle \)\frac{n}{2}">, akkor ugyanazt az ábrát kapjuk, mint ha egy csúcsból indulva minden csúcsot az (n-k)-adik szomszédjával kötjük össze. Páros n esetén \(\displaystyle k=\frac{n}{2}\) sem ad megoldást, ekkor ugyanis egyetlen szakaszt kapunk, a körülírt kör átmérőjét. Így feltehető, hogy: \(\displaystyle 2\le k<\frac{n}{2}\).

Nézzük először az n=11 esetet (ez szerepelt a kitűzésben példaként). 2\(\displaystyle \le\)k<5,5 miatt a lehetséges esetek: k=2,3,4,5. Ha k=2, a csúcsok összekötésének sorrendje:

0., 2., 4., 6., 8., 10., 1., 3., 5., 7., 9., 0.

(A 6. lépésnél nincs értelme 12. csúcsot írni, hiszen ez megegyezik az elsővel.) 11 prím, így a 11. lépésben záródik be a sokszög. A lehetséges eseteket az 5. ábra mutatja.

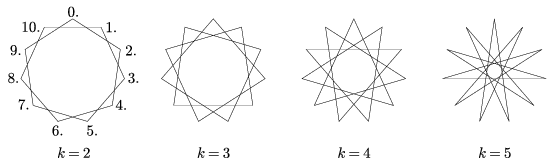
5. ábra

Hasonló igaz, ha az n prímszám. Ilyenkor a lehetséges értékek: \(\displaystyle k=2,3,\dots,\left[\frac{n}{2}\right]\) (ahol [x] jelenti az x szám egész részét, n páratlan prím, így \(\displaystyle \frac{n}{2}\) nem egész), a megoldások száma \(\displaystyle \left[\frac{n}{2}\right]-1\).

Ha n=10, akkor 2\(\displaystyle \le\)k<5 miatt a lehetséges értékek: k=2,3,4, ezeket mutatja rendre a 6. ábra. A k=2 esetben már az 5. lépésben elérjük a kiindulási pontot, anélkül, hogy a keletkezett szakaszok metszenék egymást, szabályos ötszöget kaptunk. Általánosan elmondhatjuk, hogy ha k|n, akkor szabályos \(\displaystyle \frac{n}{k}\,\)-szöget kapunk, amit a feladat nem tekint megoldásnak.

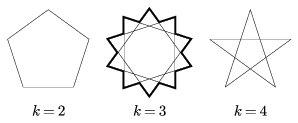
6. ábra

A k=4 esetben szabályos ötágú csillagot kapunk, ami megoldás lehetne, de a feladat szövege nem ide sorolja, n=10 esetben tízágú csillagokat kell rajzolnunk. Általánosan: ha k-nak és n-nek van közös osztója, azaz ha nem relatív prímek, akkor egy \(\displaystyle \frac{n}{(n;k)}\,\)-ágú szabályos csillagot kapunk (ahol (n;k) az n és a k legnagyobb közös osztója), ami a feladatnak nem megoldása.

A k=3 esetben valóban szabályos tízágú csillagot kapunk. Általánosan: ha k és n relatív prímek (k\(\displaystyle \ge\)2), akkor be tudjuk járni a csúcsokat anélkül, hogy az n-edik lépés előtt visszaérnénk a kiindulási pontba, a poligon hurkolt lesz és így n-ágú csillagot kapunk.

Végül n=10-re csak egy ,,jó'' megoldást kaptunk, holott ha az informatika feladatot úgy értelmezzük, hogy összekötjük a középponttól egyenlő távolságra levő átlókat, három különböző megoldást is kapnánk (hiszen ennyi lehetséges k van, 7. ábra).

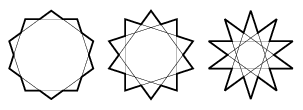
7. ábra

Van-e a feladatnak mindig megoldása, ha n nem prím? Ha n=6, k értéke csak 2 lehet, ekkor viszont szabályos háromszöget kapunk, ami nem megoldás.

Ha n legalább 3, akkor van nála kisebb hozzá relatív prím, például n-1. Mi viszont a k-nak azokkal az értékeivel dolgozunk, amelyekre k kisebb az n felénél. Láttuk, hogy ha n=6, akkor azért nincs a feladatnak megoldása, mert a 6 felénél, a 3-nál kisebb számok között csak az 1 relatív prím a 6-hoz. Vannak-e még ilyen számok? Az alábbiakban megmutatjuk, hogy nincsenek.

A következő összetett szám: n=8, ehhez a felénél kisebb relatív prím a 3. n=9 esetén megoldás a 2 (de a 4 is), n=10 esetén megoldás a 3. Képezzük most a következő szorzatot:

s_r:=p₁^.p₂^....^.p_r,

ahol p_i az i-edik prímszám. s₃=2^.3^.5=30, ami nyilván nagyobb 5-nél (a legnagyobb tényezőnél), ezért minden n-re, ahol 5<n<30, létezik k\(\displaystyle \in\){2;3;5}, hogy (k;n)=1. Ellenkező esetben ugyanis az n prímtényezős felbontásában szerepelnie kellene az első három prímnek, ám ekkor n\(\displaystyle \ge\)30. Hasonlóan kapjuk az általánosítást: Ha n kisebb az előző r prím szorzatánál, akkor a {p₁,p₂,...,p_r} halmaz valamelyik eleme és az n relatív prímek. Így ha p_r<n<s_r, akkor van olyan k\(\displaystyle \le\)p, hogy (k;n)=1. Az [5;30] intervallumban már megvizsgáltuk a 11-nél kisebb számokat, az ennél nagyobbaknál viszont az előbbiek miatt biztosan van \(\displaystyle \frac{n}{2}\)-nél kisebb n-hez relatív prím, hiszen az előző halmaz összes prím eleme kisebb 11 felénél.

Az intervallum alsó határa az r-edik prímszám, a felső határa az első r prím szorzata, ami sokkal gyorsabban nő, mint az alsó határ, így az intervallumok hossza gyorsan nő. (Pl. ha r=4, akkor ez a [7;210] intervallum; ha r=5, akkor a [11;2310].) A felső határt a második lépéstől kezdve mindig 2-nél nagyobb prímmel szorozzuk, így minden n-re találunk egy (vagy több) olyan intervallumot, amelynek tagja \(\displaystyle \frac{n}{2}\) is és n is, így az intervallumnak megfelelő prímhalmazban találunk \(\displaystyle \frac{n}{2}\)-nél kisebb n-hez relatív prímet. Tehát minden 6-nál nagyobb n esetén van informatikai feladatunknak legalább egy megoldása. A megoldások száma általában nyilván \(\displaystyle \frac{\varphi(n)-2}{2}\), ahol \(\displaystyle \varphi\)(n) jelöli az n-nél kisebb n-hez relatív számok számát. (Ehhez gondoljuk meg, hogy k és n pontosan akkor relatív prímek, ha n-k és n is azok, másfelől ha k=1 vagy n-1, akkor nem kapunk megoldást.) A fenti becslések épp azt eredményezik, hogy \(\displaystyle \varphi\)(n)>2, ha n>6.

Mindez persze nem jelenti azt, hogy hatágú csillag nem létezik, hiszen ismerünk is ilyet (8. ábra). Ezt valóban a szabályos hatszög középpontjától egyenlő távolságra lévő átlói alkotják, mégpedig az egyetlen lehetséges módon. Ha minden lehetséges csillagsokszöget szeretnénk megkapni, programozási feladatunkon úgy kellene módosítani, hogy ha visszaérünk a kiindulási pontba anélkül, hogy n-ágú csillagot kaptunk volna, az eljárást megismételjük a második pontból indulva, majd a harmadikból, és így tovább, amíg még találunk ,,szabad'' pontokat.

8. ábra

Eddigi okfejtésünk talán bonyolultnak tűnhet, de egy egyszerű programmal meg lehet keresni egy adott számhoz a felénél kisebb, vele relatív prímeket. Ezekre pedig már megalkothatjuk ,,jó'' csillagainkat.

Miklós Ildikó

Hivatkozás

[1] Hajós György: Bevezetés a geometriába, Tankönykiadó (Budapest, 1991).