Rita Kós: Conics and Dandelin spheres

By intersecting a cone with a plane - not passing through the vertex of the cone -, curves of different types can be obtained, depending on the angle enclosed between the plane and the axis of the cone. If the angle is equal to the half of the apex angle of the cone, the intersection curve is a parabola; if it is smaller than the half-angle, then the intersection is a hyperbola; if the angle is greater than the half-angle, then the curve is an ellipse; and finally, if the plane is perpendicular to the axis, then the intersection is a circle.

The curves listed above can also be considered as the loci of points of certain properties.

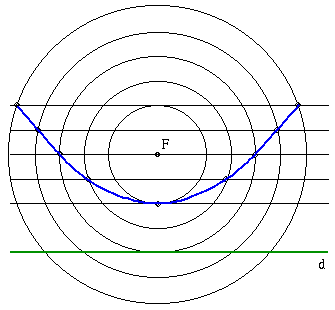
The parabola is the locus of those points in the plane that are equidistant from a fixed point, called the focus, and a fixed straight line, called the directrix.

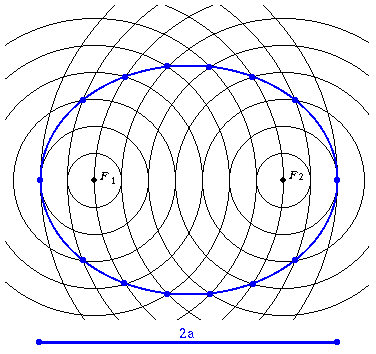
The ellipse is the locus of those points in the plane for which the sum of the distances from two given points - the so-called foci - is constant.

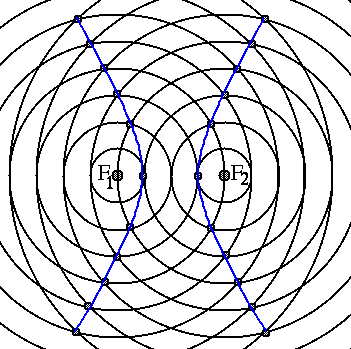
The hyperbola is the locus of those points in the plane for which the difference between the distances from two given points - the so-called foci - is constant.

The most attractive proof for the equivalence of the two types of definitions is the proof by G. P. Dandelin. His proof will be demonstrated below.

Germinal Pierre Dandelin (1794-1847) was a French engineer, who lived in Belgium. In 1822, he discovered the relation between the intersection curve of the cone with a plane, the foci of the intersecion conics, and the two inscribed spheres touching the cone and the intersecting plane.

Choose a conic to see a demonstration of the Dandelin spheres:

Ellipse

Parabola

Hyperbola