Kós Rita: Kúpszeletek és Dandelin-gömbjeik

Egy egyenes körkúpot a csúcsára nem illeszkedő síkkal elmetszve különböző görbéket kapunk síkmetszetként a szerint, hogy a sík a kúp tengelyével mekkora szöget zár be. Ha a bezárt szög megegyezik a kúp félnyílásszögével (azaz a sík egy alkotóval párhuzamos), akkor parabola, ha kisebb, mint a félnyílásszög (azaz két alkotóval párhuzamos a sík), akkor hiperbola, ha nagyobb, mint a félnyílásszög (azaz minden alkotót metsz), akkor ellipszis, ha a sík a tengelyre merőleges, akkor kör lesz a síkmetszet.

A kúpszeletekkel nagyon sok matematikus foglalkozott; a legfontosabbakat a Kúpszelet-történelem című oldalon igyekeztünk összegyűjteni.

A most megnevezett görbéket azonban inkább pontok mértani helyeként, ponthalmazként tartjuk számon.

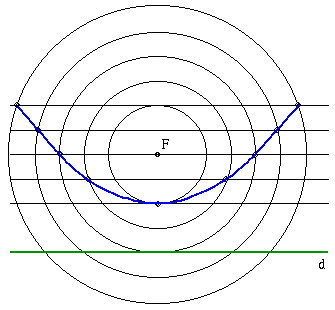
A parabola azon pontok mértani helye a síkban, amik egy adott egyenestől és egy adott (az egyenesre nem illeszkedő) ponttól egyenlő távolságra vannak.

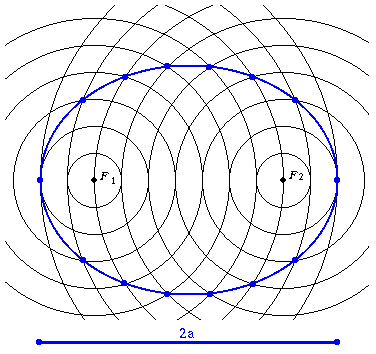
Az ellipszis azon pontok mértani helye a síkban, amelyek két adott ponttól mért távolságának összege állandó, amely állandó nagyobb az adott pontok távolságánál.

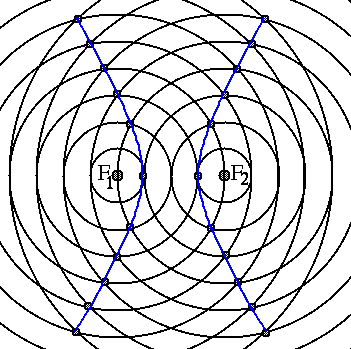
A hiperbola azon pontok mértani helye a síkban, amelyek két adott ponttól mért távolságának különbsége állandó, amely állandó kisebb az adott pontok távolságánál.

A görbék kétféle definíciójának egyenértékűségét, másszóval az azonos elnevezés jogszerűségét bizonyítani kell. A legegyszerűbb eljárást erre a bizonyítás során felhasznált érintőgömbök "feltalálójáról", Dandelinről Dandelin-gömbös bizonyításnak is nevezik. Az oldal célja, ennek minél plasztikusabb bemutatása.

Ellipszis

Parabola

Hiperbola