A 2001. évi Eötvös-verseny

Radnai Gyula, a Versenybizottság elnöke

2001. október 19-én rendezte meg az Eötvös Loránd Fizikai Társulat (ELFT) immár 85 éves múltra visszatekintő, hagyományos őszi fizikai tanulóversenyét, az Eötvös-versenyt.

A versenyen részt vehettek a 2001-ben érettségizettek, valamint a középiskolások. Délután 3^h-tól este 8^h-ig zajlott a verseny. Minden, az önálló munkához szükséges segédeszközt (magukkal hozott könyveket, jegyzeteket, zsebszámológépet) használhattak a versenyzők a feladatok megoldásához. Budapesten kívül 14 vidéki városban lehetett megírni a dolgozatot. Összesen 200 dolgozat érkezett be a Versenybizottsághoz, közülük 91-et Budapesten, 19-et Pécsett, 15-öt Szegeden, 12-t Debrecenben, 9-et Veszprémben, 5-öt Miskolcon írtak a versenyzők. A nem egyetemi városok közül Nagykanizsán írták a legtöbb (14) dolgozatot, de elég sok dolgozat (13) érkezett Békéscsabáról is. Szekszárdon 9-en, Sopronban 6-an, Székesfehérváron 3-an, Egerben 2-en adtak be dolgozatot. Sajnos Győrből és Nyíregyházáról csupán 1--1 dolgozat érkezett, Szombathelyen pedig senki se indult a versenyen.

Ismertetjük a feladatokat, a helyes megoldásokat és a verseny eredményét.

1. Két egyforma ólomgömböt egy-egy sík mentén két-két részre vágunk; egyiket az a), másikat a b) ábra szerint. A vágási felületeket hajszálvékony szigetelő réteggel látjuk el, utána a részeket újra teljes gömbbé egyesítjük. Ezután mindkét gömb bal oldali részére ugyanakkora, kicsiny Q töltést viszünk.

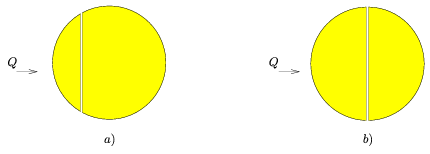
Ábrázoljuk mindkét esetben a gömb körül kialakuló erővonalképet! (A két gömb messze van egymástól, kölcsönhatásuk elhanyagolható.)

(Károlyházy Frigyes)

Megoldás. Mind az a), mind a b) esetben a bal oldali gömbszeletre vitt Q töltés a jobb oldali gömbszeleten töltésmegosztást hoz létre. Ha q-val jelöljük a Q töltésnek azt a részét, amely a feltöltött gömbszelet sík felületű részén helyezkedik el, akkor a jobb oldali gömbszelet sík felületére -q töltés vándorol, hiszen a két egymás melletti síkfelület síkkondenzátort képez (1. ábra).

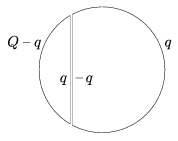
1. ábra

Vajon mekkora lesz q, és hogyan oszlanak el a töltések a gömb külső felületén? A választ pl. az energiaminimum elvéből kaphatjuk meg. Eszerint egyensúlyi helyzetben a töltések úgy helyezkednek el a vezetők felületén, hogy a rendszer teljes elektrosztatikus energiája a lehető legkisebb legyen. Jelen esetben a síkkondenzátor energiája (a szigetelőréteg hajszálvékony volta miatt) elhanyagolhatóan kicsi, a rendszer energiája tehát a gömbön kívüli elektrosztatikus mező energiájával egyezik meg. Ez az energia nyilván ugyanolyan töltéseloszlásnál lesz minimális, mint amilyen a Q töltéssel feltöltött eredeti (szétvágatlan) gömb esetében, vagyis az ismert egyenletes töltéseloszlásnál.

Más módon is érvelhetünk. Külön-külön mindkét gömbszelet potenciálja állandó, mivel elektrosztatikában a fém bármilyen alakú is legyen, mindig ekvipotenciális, s a belsejében a térerősség mindig zérus. Mennyi most a két fém-gömbszelet közti potenciálkülönbség?

$\displaystyle Delta$U=E^.d,

ahol E a két síkfelület közötti térben az elektromos térerősség, d pedig a síkfelületek távolsága. A feladat szövege szerint ez a távolság ,,hajszálvékony'', vagyis majdnem zérus, E pedig q-val arányos, tehát nem lehet ,,nagyon nagy''. Ezek szerint a $\displaystyle Delta$U potenciálkülönbség is majdnem zérus, azaz elhanyagolhatóan kicsi. Ebben a (jogos) közelítésben a teljes gömbfelület potenciálja ugyanakkora. Egyetlen gömbön az U=állandó feltétel csak egyetlen felületi töltéseloszlás mellett valósulhat meg adott Q esetén. Ez az eloszlás a jól ismert gömbszimmetrikus töltéseloszlás, amikor a felületi töltéssűrűség

$\displaystyle \sigma={Q\over4R^2\pi}={\rmállandó}.$

Az egyenletes felületi töltéssűrűséghez tartozó elektromos térerősség a gömbön belül (a ,,síkkondenzátor'' belsejét leszámítva) zérus, a gömbön kívül pedig az ismert Coulomb-féle erőtér, nagysága a középponttól r távolságban

$\displaystyle E(r)={1\over4\pi\varepsilon_0}\,{Q\over r^2}\quad($R).">

A gömbön kívül kialakuló erővonalkép tehát jó közelítéssel a 2. ábrán látható lesz.

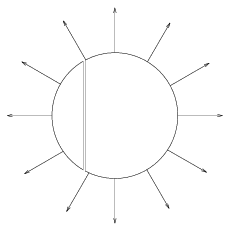
2. ábra

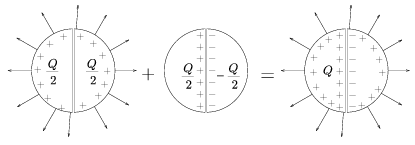
Megjegyzés: A feladatot 11 versenyző oldotta meg jól, ezen kívül még három versenyző adott be a b) kérdésre helyes megoldást. Két megoldónak{\footnote}Bartos Imre (Budapest) és Siroki László (Debrecen) jutott eszébe a középen félbevágott gömb esetére az alábbi szellemes megoldás:

Először adjunk mindkét félgömbnek Q/2 töltést, azután adjunk a bal oldalinak Q/2, a jobb oldalinak pedig -Q/2 töltést! E két állapot ,,egyesítéséből'' (szuperpozíciójából) előállítható a feladatban megadott állapot. Ez a szuperpozíció egyrészt a töltésekre, másrészt az erőtérre is vonatkozik, tehát:

2. Egy henger alakú zárt tartály fekvő helyzetben egyenletesen forog (vízszintes) hossztengelye körül, 0,5/s fordulatszámmal. A tartály 100 kg homokot tartalmaz, belső átmérője és hossza egyaránt 1 m, fala érdes.

Becsüljük meg, mennyivel növekszik a homok hőmérséklete 10 perc alatt, ha a falon keresztül elszökő hőmennyiséget elhanyagoljuk!

(Károlyházy Frigyes)

Megoldás. Ha a henger elég lassan forog (a feladatban 2 másodperc alatt fordul körbe, s ez elég lassúnak tekinthető), akkor a homok a hengerben valamennyire ,,felmászik'' a forgás irányának megfelelő oldalon, és közelítőleg egy hengerszelet térfogatát tölti ki.

A hőmérséklet változását a homok tömege, fajhője és a rajta végzett súrlódási munka ismeretében tudnánk meghatározni: $Delta$ T=W_súrl./c^.m. A homok tömege adott (m=100 kg), fajhőjét táblázatból (a hozzá hasonló anyagok, pl. a kvarcüveg vagy a porcelán adatainak felhasználásával) J/(kg^oC) egységekben 700--800 közötti értékre becsülhetjük.

A homok mozgásának részletes leírása (és ennek ismeretében a súrlódási munka kiszámítása) reménytelenül bonyolult feladat lenne. Szerencsére erre nincs szükség! Elegendő azt észrevenni, hogy az egyenletesen forgatott hengerben a homok előbb-utóbb állandósult (stacionárius) állapotba kerül. A homok egyes darabkái mozognak (áramlanak) ugyan, de a homok egésze olyan alakot vesz fel, amelynek határa időben nem változik. Emiatt a homok tömegközéppontja mindig ugyanott, a henger forgástengelyétől vízszintes irányban valamekkora k távolságra helyezkedik el (lásd az ábrát!).

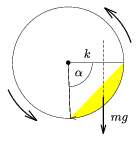
A homok belső energiájának növekedése (azaz a súrlódási erők munkája) nyilván megegyezik a henger egyenletes forgatása során végzett munkával, ez utóbbi pedig a hengerre kifejtendő mg^.k forgatónyomatéknak és a henger $Delta$ $varphi$ szögelfordulásának szorzatával egyenlő:

$\displaystyle W_{\rm s\acute url.}=mg\cdot\Delta\varphi.$

A tíz perc alatti szögelfordulás:

$\displaystyle Delta$ $varphi$ = $omega$ $Delta$ t=2 $pi$ n $Delta$ t=2 $pi$ ^.0,5 s^-1^.600 s=1885 rad.

A nehézségi erő:

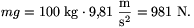
$mg=100~{\rm kg}\cdot9{,}81~{\rm m\over{\rm s}^2}=981~\rm N.$

Hátra van még a nehézségi erő k karjának kiszámítása. Becsüljük meg először a tömegközéppont és a forgástengely r_tkp távolságát! Felhasználjuk, hogy egy $alpha$ nyílásszögű hengerszelet térfogata

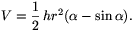
$V={1\over2}\,hr^2(\alpha-\sin\alpha).$

Jelen esetben h=10 dm, r=5 dm, így

V=m/ $varrho$ $approx$ 60-65 dm³.

(A homok sűrűsége nyilván a homok minőségétől, nedvességtartalmától, összetételétől stb. is függ, de mindenképpen kisebb, mint a tömör kvarc táblázatban megtalálható 2,65 kg/dm³-es sűrűsége.) Ezekből az adatokból és becslésekből $alpha$ $approx$ 90^o, illetve r_tkp $approx$ 4 dm adódik.

Vajon hogyan helyezkedik el a homokkal kitöltött hengerszelet síkja a henger tengelyén átmenő függőleges síkhoz képest? Mindennapi tapasztalatból (homokozó, homokóra) tudjuk, hogy a (száraz) homokból kb. 45^o-os ,,rézsűszög'' alakítható ki, ezért jogosan tekinthetjük úgy, hogy a jelen esetben is az állandósult mozgású homokgörgeteg legfelső pontja a henger tengelyével kb. azonos magasságba kerül, s emiatt a keresett erőkar

k $approx$ r_tkp^.sin45^o $approx$ 2,8 dm,

a súrlódási munkára pedig mintegy 520 J-t kapunk. Ezt felhasználva és a homok fajhőjét 800 J/(kg^oC)-nak véve kapjuk:

$Delta$ T $approx$ 6,5 ^oC.

Mivel a homok sűrűsége és fajhője is mintegy 10%-ra határozatlan mennyiség, a homok dinamikus rézsűszöge is rejt ekkora bizonytalanságot, helyesnek tekinthetünk minden olyan becslést, amely mintegy 20%-kal tér el $Delta$ T fenti értékétől, vagyis 5 és 8 ^oC közé esik.

Megjegyzések. 1. A feladat megoldása során összesen 57 versenyző jutott el odáig, hogy konkrét numerikus becslést tudott adni a hőmérséklet emelkedésére. Ezek a becslések széles határok között változtak, a legkisebb 0,0009 ^oC volt, a legnagyobb 44,65 ^oC. $Delta$ T=5--8 ^oC-os intervallumba eső értéket összesen 10 versenyző kapott, tehát ennyien oldották meg elfogadhatóan a feladatot.

2. Érdemes a feladatban leírt jelenséget kísérletileg is tanulmányozni. (A fényképen látható berendezést, amely a feladatban szereplő összeállítás kicsinyített mása, a verseny eredményhirdetésén láthattuk.) Gyorsabb forgás esetén nagyon sok érdekes részlet figyelhető meg a homokszemek ,,kollektív mozgásában''. Ezek vizsgálata ma is aktuális kutatási feladat a fizikusok számára.

3. Egy eldőlt rajzszög fekszik az enyhén lejtős asztallapon. Ha oldalról kissé meglökjük, ide-oda billeg, de nem csúszik meg. a)

Mekkora stabil egyensúlyi helyzetben a fej, illetve a tű által kifejtett erők asztalra merőleges komponenseinek aránya! b)

Mekkora frekvenciával billeg (kis kitérések esetén) a rajzszög az egyensúlyi helyzete körül?

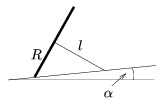
Az egyszerűség kedvéért tételezzük fel, hogy a rajzszög feje homogén körlap, tűjének tömege a fejhez képest elhanyagolható, és a tű hegye a billegés során nem mozdul el az asztallapon.

Adatok: A körlap sugara R=6 mm, a tű hossza l=8 mm, az asztal lejtése $alpha$ =5^o.

(Radnai Gyula)

Az a) kérdés sztatikai jellegű: egy merev test egyensúlyát kell tanulmányoznunk. Szerencsére az összes fellépő erő egyetlen síkban (az ábra síkjában) van, ezért könnyen felrajzolható (1. ábra).

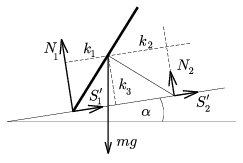
1. ábra

Jelölések: N₁ illetve N₂ az asztalra merőleges nyomóerők, S'₁ illetve S'₂ a rajzszögre ható tapadási súrlódási erők, mg (a rajzszög tömegközéppontjában ható) nehézségi erő, k₁, k₂ és k₃ a tömegközéppont távolsága a nyomóerők hatásvonalától, valamint az asztal síkjától.

A rajzszög fejét képező körlap sugara (R), a tű hossza (l) és az asztallap lejtése ( $alpha$ ) adott, ezek függvényében kell az N₁/N₂ arányt meghatároznunk. Írjuk fel a merev test egyensúlyának feltételeit!

1. 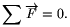$\sum{\overrightarrow{F}}=0.$ Ezt alkalmazva például az asztallappal párhuzamos összetevőkre:

S'₁+S'₂=mgsin $alpha$ ;

az asztallapra merőleges összetevőkre pedig

N₁+N₂=mgcos $alpha$ .

A fenti két egyenletből:

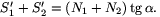
$S'_1+S'_2=(N_1+N_2)\mathop{\rm tg}\alpha.$

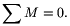2. $\sum{M}=0.$ Ez a feltétel jelen esetben csak egy összefüggést ad:

N₁k₁=N₂k₂+(S'₁+S'₂)k₃.

Behelyettesítve S'₁+S'₂ előbb kiszámított értékét:

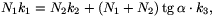
$N_1k_1=N_2k_2+(N_1+N_2)\mathop{\rm tg}\alpha\cdot k_3,$

ahonnan

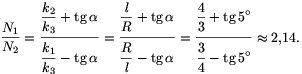
${N_1\over N_2}={\displaystyle{k_2\over\strut k_3}+\mathop{\rm tg}\alpha\over\displaystyle{\strut k_1\over k_3}-\mathop{\rm tg}\alpha}={\displaystyle{l\over\strut R}+\mathop{\rm tg}\alpha\over\displaystyle{\strut R\over l}-\mathop{\rm tg}\alpha}={\displaystyle{4\over\strut3}+\mathop{\rm tg}5^\circ\over\displaystyle{\strut3\over4}-\mathop{\rm tg}5^\circ}\approx2{,}14.$

(Természetesen ugyanilyen jó, ha valaki N₂/N₁ $approx$ 0,47-et határozza meg, illetve bármilyen más helyes úton jut a jó végeredmények valamelyikéhez.)

A b) kérdés dinamikai jellegű, s azért nehezebb, mert nem lehet síkbeli problémára visszavezetni. A rajzszög billegése nem síkmozgás, nem ,,fizikai inga''.

Készítsünk térbeli ábrát a ferde asztallapon kissé (balra) kilendített rajzszögről ( 2. ábra)!

Jelölések: K a tömegközéppont; S'₁ és S'₂ most is a tűn átmenő függőleges síkba esnek; S₁ a körlapra érintő irányban ható súrlódási erő; S₂ a tű hegyére ható súrlódási erőnek a tűre merőleges összetevője; $varphi$ a kitérés szöge (a rajzszög tűjének asztalra merőleges vetülete és a ,,lejtvonal'' által bezárt szög).


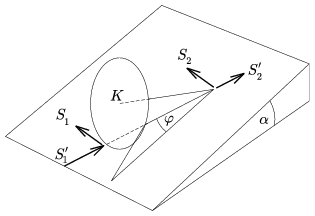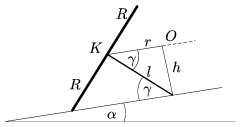2. ábra	3. ábra

A súrlódási erők mind egy síkba (az asztallap síkjába) esnek, nagyságuk változik a billegés során. A tömegközéppont pályája viszonylag egyszerű, egy körív, amelynek síkja párhuzamos az asztallap síkjával. E körív r sugara és a körív síkjának az asztallaptól mért h távolsága kiszámítható ( 3. ábra):

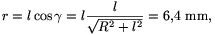
$r=l\cos\gamma=l{l\over\sqrt{R^2+l^2}}=6{,}4~\rm mm,$

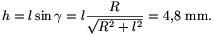
$h=l\sin\gamma=l{R\over\sqrt{R^2+l^2}}=4{,}8~\rm mm.$

(Most még nem tudjuk, hogy szükség lesz-e ezekre az adatokra, de feladatmegoldás közben mindig megnyugtató, ha már valamit ki tudunk számítani. Önbizalmat ad a továbbiakhoz.)

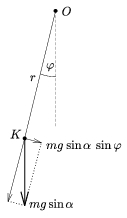
4. ábra

Vegyünk fel egy ábrát a tömegközéppont pályájának (az asztallappal párhuzamos) síkjában (4. ábra)! Itt, a pálya síkjában a K tömegközéppont mozgását a nehézségi erőnek ebbe a síkba eső mgsin $alpha$ összetevője ,,vezérli''; ezt kell felbontanunk a pálya érintője irányába mutató, illetve sugár irányú komponensekre.

Ha a kitérés $varphi$ szöge kicsi, a fonálingához hasonlóan itt is feltételezhetjük, hogy a sugár irányú gyorsulás elhanyagolható: a_cp $approx$ 0. Így a K tömegközéppont gyorsulása jó közelítéssel érintő irányú, s az r sugár $beta$ szöggyorsulásával egyszerűen kifejezhető: a_tkp=r $beta$ .

Most már nekiláthatunk a dinamikai feladat alapvető összefüggései, a mozgásegyenletek felírásához. Három mozgásegyenletünk lesz: {\noindent}

1. Gyorsul a rajzszög tömegközéppontja:

$\sum{F}=ma_{\rm tkp},$

vagyis

(1)	S₁+S₂-mgsin $alpha$ ^.sin $varphi$ =mr $beta$ .

2. Gyorsulva forog a rajzszög feje a tű körül:

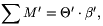
$\sum{M'}=\Theta'\cdot\beta',$

vagyis

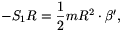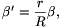
$-S_1R={1\over2}mR^2\cdot\beta',$ ahol $\beta'={r\over R}\beta,$

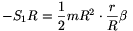(2)	$-S_1R={1\over2}mR^2\cdot{r\over R}\beta$

3. Gyorsulva elfordul a rajzszög fejének síkja a fej középpontján, valamint a fej és az asztal érintkezési pontján áthaladó tengely körül:

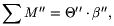
$\sum{M''}=\Theta''\cdot\beta'',$

vagyis

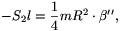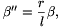
$-S_2l={1\over4}mR^2\cdot\beta'',$ ahol $\beta''={r\over l}\beta,$

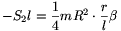(3)	$-S_2l={1\over4}mR^2\cdot{r\over l}\beta$

A megoldás további része már csak egyenletrendezés. Kifejezve S₁-et (2)-ből és S₂-t (3)-ból, behelyettesíthetjük ezeket (1)-be:

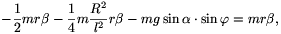
$-{1\over2}mr\beta-{1\over4}m{R^2\over l^2}r\beta-mg\sin\alpha\cdot\sin\varphi=mr\beta,$

ahonnan átrendezések után

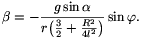
$\beta=-{g\sin\alpha\over r\big({3\over2}+{R^2\over4l^2}\big)}\sin\varphi.$

Kicsiny $varphi$ szögekre sin $varphi$ $approx$ $varphi$ , tehát itt egy

$beta$ =- $omega$ ² $varphi$

alakú összefüggést kaptunk, ami $omega$ körfrekvenciájú harmonikus rezgésnek felel meg.

A rajzszög (kis kitérésű) billegésének körfrekvenciája tehát

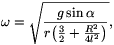
$\omega=\sqrt{g\sin\alpha\over r\big({3\over2}+{R^2\over4l^2}\big)},$

és ha ebbe behelyettesítjük 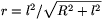$r=l^2/\sqrt{R^2+l^2}$ -et, akkor

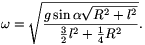
$\omega=\sqrt{g\sin\alpha\sqrt{R^2+l^2}\over{3\over2}l^2+{1\over4}R^2}.$

A megadott számadatokkal a körfrekvencia 9,02 s^-1, a frekvencia 1,44 s^-1, a periódusidő pedig T $approx$ 0,7 s lesz.

Megjegyzések: 1. A b) kérdésre csak egyetlen teljes megoldás érkezett{\footnote}Pozsgay Balázs (Budapest) dolgozata, ez sem dinamikai, hanem energetikai meggondolásokkal operált, ami persze ugyanolyan helyes. Rajta kívül még négy olyan versenyző volt, aki a körlap síkjának elfordulását elhanyagolta ugyan, de egyébként hibátlan megoldást adott. Érdemes azt is megemlíteni, hogy az a) kérdésre 82 versenyző (az indulók több, mint 40 százaléka) adott elvileg és numerikusan is helyes megoldást.

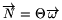2. A merev testek forgómozgásának általánosan érvényes egyenlete az $\overrightarrow{N}=\Theta\overrightarrow{\omega}$ perdületvektor időbeli változási sebességével fogalmazható meg:

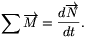
$\sum\overrightarrow{M}={d\overrightarrow{N}\over dt}.$

A perdületvektor változása egyrészt a szögsebesség változásából adódik, másrészt abból, hogy a merev test egésze elfordul, emiatt a tehetetlenségi nyomatéka az inerciarendszerből nézve időben változik. Ez utóbbiból származó perdületváltozás a szögsebesség négyzetével arányos, jelen feladatnál tehát kis kitérések esetén figyelmen kívül hagyható. A forgómozgás dinamikai egyenlete ebben a közelítésben valóban 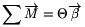$\sum\overrightarrow{M}=\Theta\overrightarrow{\beta}$ alakba írható, s ennek a vektoregyenletnek különböző komponenseit tartalmazza (2) és (3).

3. Az 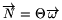$\overrightarrow{N}=\Theta\overrightarrow{\omega}$ összefüggésben szereplő 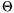$\Theta$ tehetetlenségi nyomaték nem skalár, hanem irányfüggő, ún. tenzor mennyiség. A merev testeknek csak bizonyos kitüntetett tengelyei (az ún.{\} főtengelyei) körüli forgáskor igaz az, hogy a perdületvektor és a szögsebességvektor párhuzamos egymással. A homogén korong egyik főtengelye a síkjára merőleges szimmetriatengelye (erre vonatkoztatott 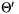$\Theta'$ tehetetlenségi nyomaték az ismert mR²/2). 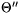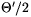A korong átmérői is főtengelyek, a hozzájuk tartozó $\Theta''$ szimmetriamegfontolások és a tehetetlenségi nyomatékot definiáló összefüggés szerint $\Theta'/2$ . Ezek az eredmények integrálszámítással is megkaphatók.

4. A szöggyorsulások közötti speciális $beta$ '=r $beta$ /R, illetve $beta$ ''=r $beta$ /l összefüggések a csúszásmentes gördülés feltételéből és térbeli geometriai megfontolásokból kaphatók meg.

A verseny végeredménye

Összevont I--II. díjat (s vele 7--7 ezer Ft pénzjutalmat) kaptak a következők: Nagy Ádám, a BME mérnök-fizikus hallgatója, aki a budapesti Szent István Gimnáziumban érettségizett mint Moór Ágnes tanítványa; Pápai Tivadar, a barcsi Dráva Völgye Középiskola 12. évf. tanulója, Horváth Ferenc tanítványa; Pozsgay Balázs, az ELTE fizikus hallgatója, aki a pécsi Magyar-német Nyelvű Iskolaközpontban érettségizett és Kotek László tanítványa volt; Siroki László, a debreceni Fazekas Mihály Gimnázium 12. évf. tanulója, Simon Gyula és Szegedi Ervin tanítványa; Tóth Sándor, a csongrádi Batsányi János Gimnázium 11. évf.{\} tanulója, Szucsán András és Hilbert Margit tanítványa; Varjú Péter, a SZTE matematikus hallgatója, aki a szegedi Radnóti Miklós Gimnáziumban érettségizett mint Dudás Zoltánné tanítványa.

III. díjat (s vele 4--4 ezer Ft pénzjutalmat) kaptak a következők: Bartos Imre, az ELTE fizikus hallgatója, aki a budapesti Móricz Zsigmond Gimnáziumban érettségizett mint Részeg Anna tanítványa; Borbély Sándor, a kolozsvári Babe{\c}s--Bolyai Tudományegyetem fizika szakos hallgatója, aki a marosvásárhelyi Bolyai Farkas Elméleti Líceumban érettségizett mint László József tanítványa; Nagy Márton, a budapesti Piarista Gimnázium 12. évf. tanulója, Futó Béla tanítványa; Novák Zoltán, a BME műszaki informatika szakos hallgatója, aki a zalaegerszegi Zrínyi Miklós Gimnáziumban érettségizett mint Vadvári Tibor tanítványa.

Dicséretet kaptak a következők: Balogh László, a Fazekas Mihály Fővárosi Gyakorló Gimnázium 11. évf. tanulója, Horváth Gábor tanítványa; Béky Bence, a Fazekas Mihály Fővárosi Gyakorló Gimnázium 12. évf. tanulója, Horváth Gábor tanítványa; Bori János Ferenc, a BME műszaki informatika szakos hallgatója, aki a budapesti Puskás Tivadar Távközlési Technikumban érettségizett mint Alapiné Ecseri Éva tanítványa; Kalcsú Áron, a zalaegerszegi Zrínyi Miklós Gimnázium 11. évf. tanulója, Pálovics Róbert tanítványa; Karaszi Mihály, a BME mérnök-fizikus hallgatója, aki a kalocsai Szent István Gimnáziumban érettségizett mint Szőke Imre tanítványa; Rácz Béla András, a Fazekas Mihály Fővárosi Gyakorló Gimnázium 10. évf. tanulója, Horváth Gábor tanítványa; Szekeres Balázs, a szolnoki Verseghy Ferenc Gimnázium 11. évf. tanulója, Lapu Béla tanítványa.

2001. november 23-án délután került sor az ünnepélyes eredményhirdetésre. Ennek során a Versenybizottság elnöke megemlékezett Bakos Tiborról (1909--1998), aki 75 évvel ezelőtt nyerte meg mind a fizikai, mind a matematikai versenyt (akkor a matematikai versenyt hívták Eötvös-versenynek, a fizikait pedig Károly Irén versenynek), s aki még 1996-ban jelen volt a díjak átadásánál. A feladatok megoldásának ismertetését azokat illusztráló kísérleti bemutató, majd az eredmények kihirdetése követte. A díjakat Gyulai József akadémikus, az ELFT elnöke adta át.

A 2001. évi Eötvös-verseny nyertesei

Alsó sor: (balról jobbra): Nagy Ádám, Pozsgay Balázs, Varjú Péter, Tóth Sándor, Siroki László és Pápai Tivadar.

Középső sor: Nagy Márton, Bartos Imre, Novák Zoltán és Borbély Sándor.

Felső sor: Rácz Béla András, Kalcsú Áron, Bori János, Balogh László, Szekeres Balázs és Karaszi Mihály.

A díjakhoz társuló jutalmakat az ELFT, illetve az Oktatási Minisztérium biztosította, a Nemzeti Tankönyvkiadó pedig valamennyi díjazott, illetve dicséretet kapott versenyzőt 3--3 ezer forintos könyvutalványban részesítette.

Az eredményhirdetés végén a nyertes versenyzők megjelent tanárai válogathattak a Nemzeti Tankönyvkiadó, a Műszaki Kiadó és a Typotex Kiadó által számukra felajánlott könyvekből.

Már regisztráltál?
Új vendég vagy?