Beszámoló a 2005. évi Eötvös-versenyről

Beszámoló a 2005. évi Eötvös-versenyről

2005. október 14-én délután az ország 16 városában rendezte meg az Eötvös Loránd Fizikai Társulat azévi Eötvös-versenyét. Budapesten 50, Pécsett 12, Debrecenben és Szegeden 7-7, Miskolcon 6, Kecskeméten 5, Veszprémben és Székesfehérváron 4-4, Győrött 1 hazai és 3 külföldi, Egerben, Szekszárdon és Szombathelyen 3-3, Békéscsabán, Nagykanizsán és Sopronban 1-1 versenyző adott be dolgozatot. Nyíregyházán sajnos egyetlen főiskolai vagy középiskolai diák se jelent meg a verseny színhelyén. Összesen 108 hazai és 4 külföldi versenyző dolgozatát kellett értékelnie a versenybizottságnak (elnök: Radnai Gyula, tagok: Gnädig Péter, Honyek Gyula és Károlyházy Frigyes).

Ismertetjük a feladatokat és a feladatok helyes megoldását.

1. Két rögzített, egymástól l=2 m távolságra levő csigán erős, de nem nyúlékony fonalat vezetünk át, és a végeire egy-egy M=1 kg tömegű testet erősítünk az 1.(a) ábra szerint. (A fonal néhányszor 10 N terhelést bír ki szakadás nélkül. A csigák és a fonal tömege elhanyagolható.) Ha ujjunkkal lehúzzuk a fonal közepét úgy, hogy a két test 1-1 méterrel megemelkedjék (1.(b) ábra), majd elengedjük, a fonal elpattan, amikor A és B között ,,kiegyenesedik''. Ha azonban úgy engedjük el, hogy előbb egy ugyancsak 1 kg tömegű testet erősítünk a fonal közepéhez, akkor a fonal a továbbiakban nem szakad el.

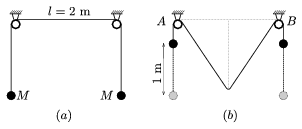
1. ábra

a) Magyarázzuk meg a jelenséget!

b) Mekkora erő feszíti a fonalat abban a pillanatban, amikor kiegyenesedik?

(Károlyházy Frigyes)

Megoldás. a) Azt kell észrevenni, hogy amikor a fonal kiegyenesedik, abban a pillanatban a fonalat két oldalról húzó testek már állnak. Rendkívül rövid idő alatt kell megállniuk, lefékeződniük arról a $\displaystyle v=\sqrt{2gh}\approx16$ km/h sebességről, amire addigi mozgásuk (szabadesés) során felgyorsultak. (Itt és a továbbiakban $\displaystyle h=\frac{1}{2}l=1~\rm m$.) Ha a fékezést ,,pillanatszerűnek'' gondolnánk, vagyis a fékezés ideje $\displaystyle \Delta$t$\displaystyle \to$0 lenne, akkor a testek gyorsulása és a fonalat feszítő F erő is minden határon túl nőne, ezért elpattanna a fonal.

A valóságban természetesen még a ,,nem nyúlékony'' fonal sem abszolút nyújthatatlan, hanem egy kicsit deformálható. Ehhez az alakváltozáshoz egy kicsiny, de véges $\displaystyle \Delta$t idő szükséges, így a testek gyorsulása és ezzel együtt a fonalat feszítő erő ha nem is végtelenné, de nagyon naggyá válik. Mivel a fonal nem bír ki nagy erőt, elszakad.

b) Ábrázoljuk a folyamat három jellemző állapotát! A 2.(a) ábrán a kezdőállapotot tüntettük fel, megjelölve közben a középső test egyensúlyi helyzetét is, amelyen maximális sebességgel átlendül. A 2.(b) ábrán a fonal középső része vízszintes, a középső test azonban még emelkedik fölfelé. A 2.(c) ábra azt a pillanatot mutatja, amikor a középső test éppen megáll. Ekkor ismét állnak a szélső testek is. (Persze elképzelhető, hogy a középső test fel se emelkedik a 2.(b) ábrán látható helyzetig, ezt a lehetőséget majd számítással kell ellenőriznünk.)

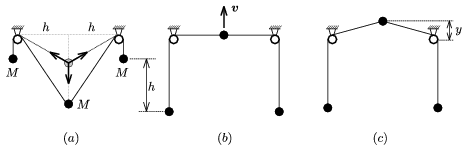
2. ábra

A b) kérdés megfogalmazása arra utal, hogy a fonal ki fog egyenesedni, tehát a középső test eljut a 2.(b) ábrán jelzett állapotba. Lesz-e ott sebessége? Ezt érdemes kiszámítanunk. Írjuk fel a munkatételt a 2.(a) helyzettől a 2.(b)-ig jelzett folyamatra! A szélső testek h utat süllyednek, a középső $\displaystyle h\sqrt{3}$ utat emelkedik, ezért

$\displaystyle Mgh-Mgh\sqrt{3}+Mgh=\frac{1}{2}\,Mv^2. $

Felhasználtuk, hogy a 2.(b) helyzetben a szélső testek egy pillanatra megállnak, ezért csak a középső testnek lehet ekkor mozgási energiája. A felírt egyenletből a középső test sebessége: $\displaystyle v=\sqrt{2g\big(2-\sqrt{3}\,\big)h$0">. Tehát valóban emelkedik még a középső test. Meddig emelkedik? Ezt is kiszámíthatjuk, ha a 2.(b) és a 2.(c) állapotot hasonlítjuk össze energetikailag:

$\displaystyle 2Mg\big(\sqrt{h^2+y^2}-h\,\big)+Mgy=\frac{1}{2}\,Mv^2. $

Ez y-ra nézve másodfokú egyenletté alakítható, melynek megoldásai: y₁=-1,73 h és y₂=+0,22 h. (Az első gyök nyilván a kezdőállapotot adja meg, a 2.(c) állapotnak y₂ felel meg.)

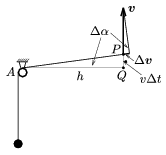
3. ábra

Hogy válaszolni tudjunk a feladat b) kérdésére, vizsgáljuk meg tüzetesen a 2.(b) ábrán látható helyzetet! Ebben a pillanatban a fonalat feszítő erő gyorsítja az éppen álló, de felfelé induló szélső testeket. Mekkora ez a gyorsulás? Tegyük fel, hogy a bal oldali csigától a középső testhez vezető AP fonál $\displaystyle \Delta$t idő alatt már egy kicsiny $\displaystyle \Delta$ $\alpha$ szöggel túllendült a vízszintes helyzeten (3. ábra). Jelöljük a szélső testek sebességét $\Delta$ v-vel! Ez a sebesség (a fonal nyújthatatlansága miatt) megegyezik a P pontban levő középső test sebességének AP irányú vetületével, vagyis

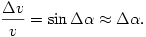
$\frac{\Delta v}{v}=\sin\Delta\alpha\approx\Delta\alpha.$

Másrészt a PQA derékszögű háromszögből

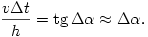
$\frac{v\Delta t}{h}={\rm tg}\,\Delta\alpha\approx\Delta\alpha.$

A fenti két egyenlet összevetéséből

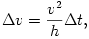
$\Delta v=\frac{v^2}{h}\Delta t,$

vagyis a szélső testek gyorsulására

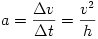
$a=\frac{\Delta v}{\Delta t}=\frac{v^2}{h}$

adódik.

Ugyanehhez a képlethez úgy is eljuthatunk, ha felírjuk, hogy a vízszinteshez közeli AP szakasz hossza időben hogyan változik. Mivel PQ $\approx$ vt (ahol t a 2.(b) ábrán látható állapottól mért idő), Pitagorasz tétele szerint

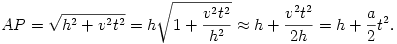
$AP=\sqrt{h^2+v^2t^2}=h\sqrt{1+\frac{v^2t^2}{h^2}}\approx h+\frac{v^2t^2}{2h} =h+\frac{a}{2}t^2.$

Ebből leolvashatjuk, hogy az AP szakasz hossza a=v²/h gyorsulással növekszik, s a fonal nyújthatatlansága miatt a bal oldali test is ugyanekkora nagyságú, függőlegesen felfelé irányuló gyorsulással kell rendelkezzék.

A fonal által kifejtett erő a szélső testek mozgásegyenletéből kapható meg:

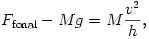
$F_{\text{fonal}}-Mg=M\frac{v^2}{h},$

azaz

$F_{\text{fonal}}=Mg\big[1+2\big(2-\sqrt{3}\,\big)\big]=1{,}536\,Mg\approx15~\rm N.$

Így már érthető, miért nem szakad el ebben a helyzetben a ,,néhányszor 10 N terhelést kibíró'' fonal.

Érdemes felfigyelni arra, hogy a szélső testek kétszer is emelkednek és kétszer is süllyednek egy-egy periódus során, hiszen a 2. ábrán feltüntetett mindhárom állapotban éppen állnak. Süllyedésük az idő függvényében nagyjából a 4. ábrán vázolt módon történik.

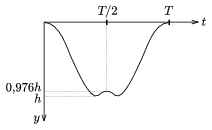
4. ábra

2. Egy átlátszatlan lapon kicsiny lyukak vannak az 5. ábrán látható ,,háromszög-rács'' elrendezésben. A lapot monokromatikus, $\lambda$ hullámhosszúságú lézerfénnyel világítjuk meg merőlegesen. A rácsállandó d=100 $\lambda$ .

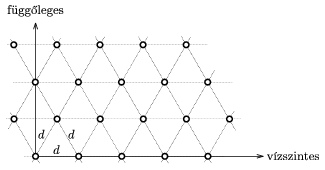
5. ábra

Ábrázoljuk vázlatosan (a méretek, valamint a vízszintes és a függőleges irányok bejelölésével), hogy milyen elhajlási képet figyelhetünk meg a rácstól 3 m távolságra elhelyezett ernyőn!

(Gnädig Péter)

Megoldás. Elevenítsük fel azokat az ismereteket, amelyek a síkbeli optikai rácson (párhuzamos, egymástól egyenlő távolságra lévő rések rendszerén) áthaladó monokromatikus fény diffrakciójára vonatkoznak! Világítsuk meg az optikai rácsot a síkjára merőleges, keskeny lézersugárral. A ráccsal párhuzamosan elhelyezett ernyőn ekkor közelítőleg egyenlő távolságra elhelyezkedő fényes foltokat látunk. Jelöljük D-vel a rácsállandót, $\lambda$ -val a hullámhosszat. Az intenzitás menetét az elhajlási (diffrakciós) szög szinuszának függvényében a 6. ábra mutatja.

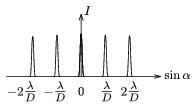
6. ábra

Az ábrán látható intenzitáseloszlást jól alátámasztja az a középiskolában tanult közelítés, amely szerint a rács rései olyan keskenyek, hogy egy-egy résen belül, az onnan kiinduló elemi hullámok azonos fázisban vannak (Huygens-Fresnel-elv). Ugyanakkor két egymás melletti résből induló elemi hullámok erősítésének feltétele:

D sin $\alpha$ _k=k $\lambda$ (k=0, $\pm$ 1, $\pm$ 2,...).

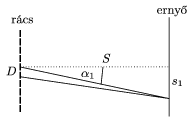
7. ábra

Ha az ernyő S távolságra van az optikai rácstól (7. ábra), akkor az első főmaximum távolsága a centrumtól

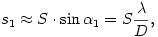
$s_{1}\approx S\cdot\sin\alpha_{1}=S\frac{\lambda}{D},$

és általában, a k-adik főmaximum távolsága

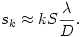
$s_{k}\approx kS\frac{\lambda}{D}.$

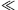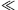(Itt kihasználtuk, hogy $\lambda$ $\ll$ d miatt $\alpha$ _k $\ll$ 1, és így sin $\alpha$ _k $\approx$ $\alpha$ _k.)

Térjünk rá a feladatban szereplő háromszögrácsra! Mivel a háromszögrács síkjára merőlegesen érkezik a fény, ezért minden egyes lyukból azonos fázisú elemi hullámok indulnak ki. Ezek a rácsra merőleges irányban tovább haladva biztosan erősítik egymást, útkülönbség nélkül, $\alpha$ =0 irányban jelölik ki a keletkező diffrakciós kép centrumát az elég távol lévő ernyőn.

Hol lesz ehhez a centrumhoz legközelebb újra egy erősítési hely az ernyőn? Milyen irányban?

Válasszuk ki valamelyik kicsiny lyukat. Gondolatban húzzunk ezen a lyukon át egy olyan egyenest, amelyik átmegy valamelyik, hozzá legközelebb eső lyukon. Ez az egyenes még egy sorozat lyukon fog áthaladni, amelyek mind d távolságra követik egymást. Most keressünk egy másik lyuksort, amelyen átmenő egyenes párhuzamos az előzővel. Sok ilyen lyuksort találunk, ezek egymástól 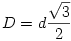$D=d\frac{\sqrt{3}}{2}$ távolságra helyezkednek el (8. ábra). Figyeljük meg azt az irányt a térben, amely az elképzelt egyenesekre merőleges, de a már kijelölt centrum felé vezető iránnyal akkora $\alpha$ ₁ szöget zár be, hogy teljesül a

Dsin $\alpha$ ₁= $\lambda$

összefüggés.

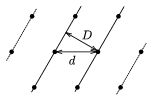
8. ábra

Ha az ilyen irányba haladó elemi hullámok eredőjét vizsgáljuk a messze lévő ernyőn, akkor azt látjuk, hogy a kiválasztott egyenesen elhelyezkedő lyukakból jövő elemi hullámok erősítik egymást, mert az ernyőhőz érve már szinte nincs is útkülönbség köztük. De a szomszédos egyenesen fekvő lyuksorból induló elemi hullámokkal is erősíteni fogják egymást, mert köztük az útkülönbség (Dsin $\alpha$ ₁) éppen $\lambda$ -val egyenlő, és ugyanez igaz a többi egyenesen fekvő lyukakból induló hullámokra is. Tehát ebben az irányban az összes lyukon átjövő fény erősíteni fogja egymást!

Így az ernyőn a centrumhoz legközelebbi (egyik) erősítési helynek a centrumtól való távolsága:

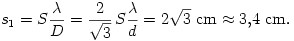
$s_{1}=S\frac{\lambda}{D}=\frac{2}{\sqrt{3}}\,S\frac{\lambda}{d}=2\sqrt{3}~{\rm cm}\approx3{,}4~{\rm cm}.$

Hat ilyen pont lesz az ernyőn, amelyek egy - a centrum körüli - szabályos hatszög csúcsait jelölik ki. Ez azért van így, mert három, egymással 120-120^o-os szöget bezáró egyenes-sereget (lyuksor-sereget) jelölhetünk ki a háromszögrácson.

Azt is észrevehetjük, hogy olyan helyen is lesz az ernyőn erősítés, melynek távolsága a centrumtól 2s₁, 3s₁,..., hiszen ekkor az egymás melletti lyuksorokból érkező hullámok 2 $\lambda$ , 3 $\lambda$ ,... útkülönbséggel találkoznak az ernyőn. Ezek szerint a rácson felvett mindegyik egyenes-sereg az ernyőn egy pontsorozatot eredményez. Ha a rácson elképzelt lyuksorok pl. vízszintes egyenesek mentén helyezkednek el, akkor az ernyőn keletkező pontsorozat egy függőleges egyenesre illeszkedik.

Hatágú ,,csillag'' lesz tehát a kép? Nem egészen, bár ezek a most elképzelt pontok mind megjelennek az ernyőn, de nem csak ezek jelennek meg! Képzeljük el például a háromszögrácson azt az egyenes- (lyuksor)-sereget, amelyet a 9. ábra bal oldalán látunk.

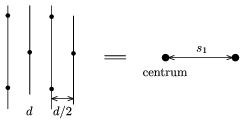
9. ábra

Ez egy 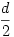$\frac{d}{2}$ rácsállandójú optikai rácsnak felel meg, ezért az ernyőn a megfelelő erősítési helyek

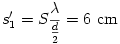
$s_{1}'=S\frac{\lambda}{\frac{d}{2}}=6~\rm cm$

távolságra követik egymást. Most is igaz, hogy minél sűrűbb optikai rácsba rendeződve képzeljük el a lyukakat, annál messzebb kerülnek egymástól a megfelelő erősítési helyek az ernyőn.

Meg lehet mutatni, hogy a háromszögrács ,,képe'' az ernyőn ugyancsak szabályos háromszögrács lesz, mert kölcsönösen egyértelműen egymáshoz rendelhető a lyukakra illeszthető egyenessereg és az ernyőn megjelenő, interferencia eredményezte ponthalmaz. (Ennek belátásához legközelebb Varjas Dániel jutott el, aki díjnyertes dolgozatában a különböző módon felvehető elemi cellák területének egyenlőségét használta ki.) Mégis lesz valami eltérés a lyukak alkotta háromszögrács és a diffrakciós pontok alkotta háromszögrács között (a pontok távolságában mutatkozó eltérésen kívül is): az egyik pontrács 90^o-os elforgatottja a másiknak. (Most akár 30^o-os elforgatottat is mondhatnánk, de egy téglalaprács esetén nagyon jól látszik, hogy 90^o-os elforgatásról van szó.)

Mindezt a 10. ábra szemlélteti, melynek jobboldali részén a lyukak rácsa, a baloldalin pedig az ernyőn látható elhajlási kép látható, természetesen eltérő méretarányban.

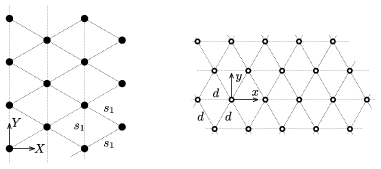
10. ábra

A feladatban szereplő háromszögrácsot úgy is előállíthatjuk, hogy három, egyenként D állandójú, közönséges optikai rácsot egymásra fektetünk. A feltétel csak annyi, hogy mindegyik rács rései a másik rács réseivel 60^o-os szöget zárjanak be. Az így keletkező lyukak ugyan nem kör, hanem hatszög alakúak lesznek, de ha a rések szélessége sokkal kisebb a rácsállandónál, akkor ennek nincs jelentősége. Sőt! Ha elhagyjuk a harmadik rácsot, és csupán két, egymással 60^o-os szöget bezáró rács diffrakciós képét vizsgáljuk, ez is ugyanaz lesz, mint az előbbiek. Ebben az esetben ugyanis a lyukak ugyan rombusz alakúak, de ugyanabban a szabályos háromszögrácsban rendeződnek el, tehát jó közelítésben ugyanazt a diffrakciós képet eredményezik. Az eredményhirdetéskor Komlósi István egyetemi hallgató mutatta be ezt a kísérletet.

3. Egy jó minőségű transzformátor szekunder tekercsének menetszáma háromszorosa a primer tekercsének. Ezt a trafót a 11. ábra szerint hálózati váltóáramú feszültségforrásra kapcsoljuk a következő módon: A primer körbe egymással párhuzamosan iktatunk be öt egyforma, a hálózati feszültségre méretezett izzó közül négyet, az ötödiket a szekunder körbe kötjük. Mi történik a K kapcsoló zárása után?

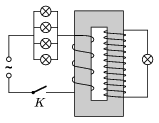
11. ábra

a) Mindegyik izzó tűrhetően ég.

b) A primer körbeli négy izzó szépen ég, az ötödik legfeljebb pislákol.

c) A szekunder körbeli izzó egy pillanat alatt kiég, utána a primer körbeli izzók sem világítanak, mivel a primer tekercs fojtótekercsként hat.

Melyik a helyes válasz?

(Károlyházy Frigyes)

Megoldás. Ezt a feladatot is többféleképpen lehet megoldani. Eljuthatunk a helyes válaszhoz okoskodással, analógiák felhasználásával, úgy, ahogy például az előző feladat megoldásának bemutatásakor jártunk el. Most más utat választunk: bemutatjuk a lehető legrövidebb utat, ahogy a megoldást megkaphatjuk.

Ismert - szakkönyvekben, példatárakban megtalálható, így az Eötvös-versenyen szabadon felhasználható - a transzformátor helyettesítő kapcsolása, ami a 12. ábrán látható.

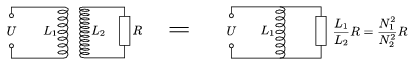
12. ábra

Első közelítésben tekintsünk el attól, hogy az izzók ellenállása függ a rajtuk áthaladó áramtól (erre még visszatérünk), és induljunk ki abból, hogy van öt egyforma ellenállásunk. Az eredő a szekunder oldalon R, primer oldalon R/4, a párhuzamos kapcsolás miatt. Mivel a szekunder tekercs menetszáma háromszorosa a primer tekercsének, ezért a helyettesítő kapcsolásban ide R/9 ellenállás kerül (13. ábra).

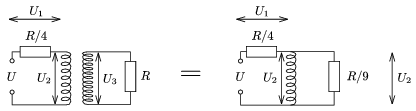
13. ábra

Egy jó minőségű transzformátor szekunder tekercsének váltóáramú ellenállása sokkal nagyobb, mint az izzó ellenállásának kilenced része, ezért jó közelítésben írhatjuk:

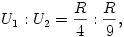
$U_{1}:U_{2}=\frac{R}{4}:\frac{R}{9},$

valamint U₁+U₂=U és U₃=3U₂. Ezekből az összefüggésekből következik:

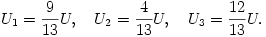
$U_{1}=\frac{9}{13}U,\quad U_{2}=\frac{4}{13}U,\quad U_{3}=\frac{12}{13}U.$

A primer tagban egy-egy izzóra jutó teljesítmény:

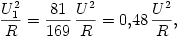
$\frac{U_{1}^2}{R}=\frac{81}{169}\,\frac{U^2}{R}=0{,}48\,\frac{U^2}{R},$

durván fele annak a teljesítménynek, amellyel a hálózati feszültségen világítanának. A szekunder körben az izzó teljesítménye:

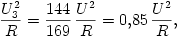
$\frac{U_{3}^2}{R}=\frac{144}{169}\,\frac{U^2}{R}=0{,}85\,\frac{U^2}{R},$

nincs nagyon messze attól a teljesítménytől, amellyel ez az izzó a hálózati feszültségen világítana.

Ha most figyelembe vesszük azt a tényt, hogy alacsonyabb feszültségen (tehát alacsonyabb hőmérsékleten) az izzó ellenállása is kisebb, azt mondhatjuk, hogy a primer ágban levő izzók ténylegesen nagyobb teljesítménnyel világítanak, mint amit most kiszámítottunk.

Bátran állíthatjuk, hogy mindegyik izzó tűrhetően ég, vagyis az a) válasz a helyes.

Azok számára, akik járatosak a szinuszos váltóáramú hálózatok komplex számokat felhasználó számításaiban, megmutatjuk a 12. ábrán látható két kapcsolás egyenértékűségét, melyet a megoldásban felhasználtunk. A transzformátor primer és szekunder körére felírhatjuk:

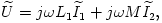
$\widetilde{U}=j\omega L_{1}\widetilde{I_{1}}+j\omega M\widetilde{I_{2}},$

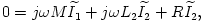
$0=j\omega M\widetilde{I_{1}}+j\omega L_{2}\widetilde{I_{2}}+R\widetilde{I_{2}},$

ahol 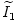$\widetilde{I_{1}}$ a primer-, 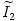$\widetilde{I_{2}}$ a szekunder körben folyó áram komplex alakja, M pedig a két tekercs kölcsönös indukciós együtthatója. A második egyenletből 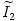$\widetilde{I_{2}}$ -t kifejezve és az első egyenletbe helyettesítve, valamint felhasználva a szoros csatolás esetén érvényes M²=L₁L₂ összefüggést, rendezés után kapjuk:

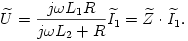
$\widetilde{U}=\frac{j\omega L_{1}R}{j\omega L_{2}+R}\widetilde{I_{1}} =\widetilde{Z}\cdot\widetilde{I_{1}}.$

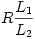A helyettesítő kapcsolásban j $\omega$ L₁ és $R\frac{L_{1}}{L_{2}}$ váltóáramú ellenállások párhuzamos eredőjét kell kiszámítanunk:

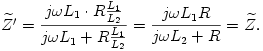
$\widetilde{Z'}=\frac{j\omega L_{1}\cdot R\frac{L_{1}}{L_{2}}}{j\omega L_{1}+R\frac{L_{1}}{L_{2}}}=\frac{j\omega L_{1}R}{j\omega L_{2}+R}=\widetilde{Z}.$

Éppen ez az, amit be akartunk bizonyítani.

A verseny eredménye

A verseny ünnepélyes eredményhirdetésére és a díjkiosztásra 2005. november 25-én délután került sor az ELTE Mogyoródi József termében.

Bevezetésként a versenybizottság elnöke emlékezett vissza az 50 évvel ezelőtti és a 25 évvel ezelőtti versenyre. Írásvetítőn kivetítette az 50 évvel korábbi feladatokat, valamint az akkori nyertesek egy-egy KöMaL feladatra adott egykori megoldását. A feladatokat Kárteszi Ferenc, illetve Prékopa András tűzte ki (akkor még nem volt fizika rovat a KöMaL-ban). Aki a versenyt megnyerte, Bártfai Pál matematikus, ma a Kürschák-verseny zsűrijének oszlopos tagja. Elfogadta meghívásunkat, személyesen (családosan!) megjelent az eredményhirdetésen, és néhány mondatban felelevenítette emlékeit. Nem csak a versenyről beszélt, hanem a felkészülésről is, Vermes tanár úr szakköréről, melynek oly sokat köszönhetett fizikából. Utána az elnök az 50 évvel ezelőtti második helyezett, az Egyesült Államokban élő Gutai László fizikus levelét olvasta fel. Ő is megemlékezett egykori tanáráról, Varga Zoltánról, aki őt Újpesten tanította. A 25 évvel ezelőtti Eötvös-verseny nyertesek közül Szalontai Zoltán és Umann Gábor jelent meg, mindketten a KöMaL szorgalmas feladatmegoldói voltak, négy éven át jelent meg fényképük a legjobb megoldók között. Ezeket a képeket egymás mellé vetítve láthatták most a megjelentek.

Ezek után került sor a feladatok fent leírt megoldásának ismertetésére. Mindegyik feladathoz kapcsolódott kísérlet is: az elsőt Honyek Gyula, a másodikat és a harmadikat Gnädig Péter mutatta be.

Következtek az ünnepélyes eredményhirdetés legizgalmasabb pillanatai: az elnök Patkós András akadémikust, az Eötvös Loránd Fizikai Társulat elnökét kérte fel a díjak és az oklevelek átadására.

I. díjat, a vele járó Eötvös-verseny érmet és 20 ezer forintos jutalmat kapta Varjas Dániel, a BME mérnök-fizikus hallgatója, aki a dunaújvárosi Széchenyi István Gimnáziumban érettségizett mint Kispál István tanítványa. Varjas Dániel tavaly is első díjat kapott az Eötvös-versenyen, így hát ő az első az országban, aki két Eötvös-verseny éremmel is rendelkezik. Nehéz volt megmondani, hogy ő, vagy Kispál tanár úr hatódott-e meg jobban, amikor kiderült, hogy Dani nyert a versenyen.

A versenybizottság döntése értelmében hárman kaptak II. díjat és vele 14 ezer forint jutalmat, ketten III. díjat és vele 12 ezer forint jutalmat, valamint hat versenyzőt részesített a zsűri dicséretben:

II. díjasok: Halász Gábor, az ELTE Radnóti Miklós Gyakorló Gimnáziumának 12. osztályos tanulója, Honyek Gyula tanítványa; Kómár Péter, az ELTE fizikus hallgatója, aki a Fazekas Mihály Fővárosi Gyakorló Gimnáziumban érettségizett mint Dvorák Cecília tanítványa és Szolnoki Lénárd, a Debreceni Református Kollégium Dóczy Gimnáziumának 10. osztályos tanulója, Tófalusi Péter tanítványa.

III. díjasok: Kónya Gábor, a Fazekas Mihály Fővárosi Gyakorló Gimnázium 11. osztályos tanulója, Horváth Gábor tanítványa és Széchenyi Gábor, a szolnoki Verseghy Ferenc Gimnázium 12. osztályos tanulója, Pécsi István tanítványa.

Dicséretet kapott Farkas Ádám László, a miskolci Földes Ferenc Gimnázium 11. osztályos tanulója, Zámborszky Ferenc tanítványa; Ferenczy Máté, a BME mérnök-fizikus hallgatója, aki a Fazekas Mihály Fővárosi Gyakorló Gimnáziumban érettségizett mint Dvorák Cecília tanítványa; Németh Balázs, a székesfehérvári Tóparti Gimnázium 11. osztályos tanulója, Tóthné Rohovszky Katalin tanítványa; Pálinkás András, az ELTE fizikus hallgatója, aki a budapesti Piarista Gimnáziumban érettségizett mint Futó Béla tanítványa; Paulin Roland, a Fazekas Mihály Fővárosi Gyakorló Gimnázium 12. osztályos tanulója, Horváth Gábor tanítványa és Végh Sándor, a Debreceni Egyetem Kossuth Lajos Gimnáziumának 12. osztályos tanulója, Kirsch Éva és Szegedi Ervin tanítványa.

A nyertes versenyzők tanárai, akik szintén meghívót kaptak az ünnepélyes díjkiosztásra, a Typotex Kiadó által erre a célra felajánlott könyvek közül válogathattak.

Végül Patkós András akadémikus elevenítette fel az Eötvös-versennyel kapcsolatos régebbi és legújabb emlékeit, benyomásait (lásd a hátsó belső borítón középen jobbra). Utána közös fényképezkedés következett, melyen az 50 és a 25 évvel ezelőtti nyertes fogta közre az idei első díjast, s egy jó hangulatú baráti beszélgetésben folytatódott az egymást eddig java részt csak hírből ismerő meghívottak társalgása. A Ramasoft Rt. jóvoltából üdítő és finom szendvicsek is jutottak a végig ott maradóknak.

Radnai Gyula

Már regisztráltál?
Új vendég vagy?