Beszámoló a 2008. évi Eötvös-versenyről

Radnai Gyula

Vermes Miklós ,,Az Eötvös-versenyek feladatai 1959-1988'' c. könyvében írja: ,,A háború utáni versenyek 1949-ben indultak meg újra, és azóta Eötvös-verseny néven rendezik meg minden ősszel.'' Minthogy azóta is minden évben sikerült megtartani a versenyt, 2008-ban volt a háború utáni 60. Eötvös-verseny.

A Versenybizottságban Károlyházy Frigyes több, mint 40 éve, Radnai Gyula 35 éve, Gnädig Péter 20 éve, Honyek Gyula 5 éve vesz részt. 1987-ig Vermes Miklós, 1988-tól Radnai Gyula az elnöke a Versenybizottságnak.

A 2008. október 17-én délután 3 és este 8 óra között tartott versenyen Budapesten 40, a 14 vidéki városban összesen 59 versenyző adott be dolgozatot. Valamennyien hazai középiskolába jártak vagy járnak, külföldi versenyző nem volt. A Fazekas Mihály Fővárosi Gyakorló Gimnáziumból 15-en indultak, többen, mint akármelyik vidéki városból. Sajnos két helyszínről, Kecskemétről és Székesfehérvárról egyetlen dolgozat sem érkezett. A viszonylag alacsony részvételi létszám jól tükrözi a fizika tantárgy országosan nehéz helyzetét, ugyanakkor a legjobb tíz dolgozat átlagos színvonala ugyanolyan magas volt, mint az elmúlt években - méltón az Eötvös-verseny hagyományaihoz.

1. feladat. Egy cirkuszi egyensúlyozóművész egy hosszú függőleges rúdra akar felmászni. A rúd hossza \(\displaystyle \ell\), tömege m. A produkció kezdetekor a rudat az egyik végéhez erősített, elhanyagolható súlyú rugalmas kötélen engedik le a cirkusz kupolájától. Amikor a rúd alja éppen a talajhoz ér, a kötél 2\(\displaystyle \ell\) hosszú (1. ábra). A kötél nyújtatlan hossza \(\displaystyle \ell\), megnyúlása közben jól követi a Hooke-törvényt.

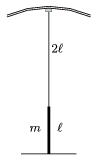
1. ábra

a) Milyen magasra mászhat fel a rúdra az ugyancsak m tömegű artista anélkül, hogy a rúd függőleges egyensúlyi helyzete instabillá válna? (Az egyszerűség kedvéért tételezzük fel, hogy az artista mérete \(\displaystyle \ell\)-hez képest elhanyagolható.)

b) A rúd fele magasságánál az artista kicsit kibillen és a rúddal együtt oldalirányú lengésekbe kezd. Mekkora a lengés T periódusideje? (A rúd alsó vége nem tud elmozdulni, de a rúd szabadon elfordulhat az alsó végpontja körül.)

(Balogh Péter)

Megoldás. Azoknak a versenyzőknek sikerült jól megoldaniuk ezt a feladatot, akik elég bátrak voltak, és már kezdetben figyelembe vették, hogy elegendő az artista kicsiny kibillenését vizsgálni. Ők azután nem tévedtek el a tetszőleges szögekre érvényes, bonyolult összefüggések erdejében.

A 2. ábrán a hosszakat, a 3. ábrán az erőket ábrázoltuk az \(\displaystyle \alpha\) szöggel kibillent rúd esetében. Ekkor a kötélnek a függőlegessel bezárt szöge \(\displaystyle \beta\). Ha figyelembe vesszük, hogy kicsiny szögekről van szó, jó közelítéssel írhatjuk:

\(\displaystyle \beta\approx\frac{\alpha}{2}. \)

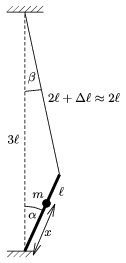
2. ábra

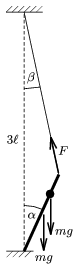
3. ábra

A kilendült rudat a rúdra és az artistára ható nehézségi erő tovább akarja lendíteni, a kötél rugalmassága pedig visszahúzza. A nehézségi erők forgatónyomatékának nagysága (a rúd alsó végpontjára):

\(\displaystyle M_{1}=mg\frac{\ell}{2}\sin\alpha+mgx\sin\alpha\approx\)

\(\displaystyle \approx mg\left(\frac{\ell}{2}+x\right)\alpha,\)

a visszahúzó kötélerő forgatónyomatékának nagysága pedig

\(\displaystyle M_{2}=F\ell\sin\,(\alpha+\beta)\approx F\ell(\alpha+\beta)\approx F\ell\frac{3}{2}\alpha. \)

A stabilitás feltétele:

M₂>M₁.

Felhasználva, hogy kis szögekről van szó:

\(\displaystyle F\ell\frac{3}{2}\alph\)mg\left(\frac{\ell}{2}+x\right)\alpha. ">

Ha eltekintünk a kötél kicsiny, további megnyúlásától, F továbbra is jó közelítéssel mg nagyságú marad. (F kicsiny megváltozását az ugyancsak kicsiny \(\displaystyle \alpha\)-val szorozva másodrendűen kicsiny tagot kapunk, amit elhanyagolunk.) Ezt felhasználva a stabilitási feltétel:

\(\displaystyle mg\ell\frac{3}{2}\alph\)mg\left(\frac{\ell}{2}+x\right)\alpha,">

\(\displaystyle \frac{3}{2}\el\)\frac{\ell}{2}+x,">

x <\(\displaystyle \ell\).

Tehát az artista felmászhat egészen a rúd tetejéig, amíg csak x<\(\displaystyle \ell\) teljesül. Ezzel válaszoltunk az a) kérdésre, most foglalkozzunk a b)-vel.

Tekintsük a 4. ábrát, amelyen már figyelembe vettük a \(\displaystyle \beta\approx\frac{\alpha}{2}\) közelítést, mivel továbbra is kis szögkitérésű lengésekről lehet csak szó, továbbá azt, hogy most \(\displaystyle x=\frac{\ell}{2}\). A visszatérítő forgatónyomaték:

\(\displaystyle M=M_{2}-M_{1}=F\ell\,\frac{3}{2}\alpha-2mg\,\frac{\ell}{2}\alpha=\ell\alpha\left(\frac{3}{2}F-mg\right)=\)

\(\displaystyle =\frac{1}{2}mg\ell\cdot\alpha.\)

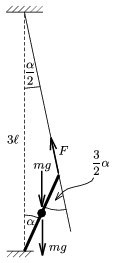
4. ábra

Ez a visszatérő forgatónyomaték egyenesen arányos \(\displaystyle \alpha\)-val! Ebben az esetben harmonikus rezgés (lengés) jöhet létre, melynek periódusidejét az arányossági tényezőből olvashatjuk ki. A rúdból és az artistából álló rendszer teljes tehetetlenségi nyomatéka (a rúd legalsó pontjára vonatkoztatva):

\(\displaystyle \Theta=\frac{1}{3}m\ell^2+m\left(\frac{\ell}{2}\right)^{2}=\frac{7}{12}\,m\ell^2. \)

A harmonikus rezgőmozgásnál, ahol a visszahúzó erő nagysága F=Dx, fennáll a következő összefüggés:

\(\displaystyle \omega^2=\frac{D}{m}=\frac{F/x}{m}\,. \)

Ezzel analóg módon a lengésekre (harmonikusan változó forgómozgásra)

\(\displaystyle \omega^2=\frac{M/\alpha}{\Theta}= \frac{\frac{1}{2}\,mg\ell}{\frac{7}{12}\,m\ell^2}=\frac{6}{7}\,\frac{g}{\ell} \)

érvényes. Ebből a lengés periódusideje:

\(\displaystyle T=2\pi\sqrt{\frac{7}{6}\,\frac{\ell}{g}}\,, \quad\mbox{mivel}\quad T=\frac{2\pi}{\omega}\,. \)

2. feladat. Ugyanabból az anyagból készült, állandó fajhőjű három test hőmérséklete 13 ^oC, 27 ^oC és 90 ^oC. A két melegebb test tömege egyenként fele a 13 ^oC-os test tömegének. Megfelelő hőgépek és energiatároló eszközök közbeiktatásával, külső energia befektetése nélkül szeretnénk a 13 ^oC-os testet minél jobban lehűteni.

a) Hogyan kell eljárnunk? (A testek csak hőfelvétel vagy hőleadás során változtathatják meg hőmérsékletüket, halmazállapotváltozás nem történik, hőtágulásuk elhanyagolható.)

b) Mennyire hűlhet le az eredetileg 13 ^oC-os test?

(Radnai Gyula)

Megoldás. a) Hogyan lehet három test közül a leghidegebbet még tovább hűteni? Nincs nála hidegebb test, amivel kapcsolatba hozhatnánk. Adiabatikus munka végzésére sincs lehetőség, a testek most csak hőfelvétel vagy hőleadás során változtathatják meg a hőmérsékletüket.

Semmi kétség: hűtőgépre van szükségünk! Viszont minden hűtőgép működtetéséhez külső energiaforrás kell, ami most nem áll rendelkezésre.

Illetve mégis van egy kiút: ha a két különböző hőmérsékletű másik test felhasználásával működtetünk egy hőerőgépet! Azt a munkát, amit ebből nyerünk, felhalmozzuk egy energiatárolóban. Mire a két melegebb test között végül megszűnik a hőmérsékletkülönbség, az így előállt ,,középmeleg'' test és a hideg test közé már beiktathatunk egy hűtőgépet, amely az előbb nyert munka befektetésével biztosan működik valameddig. Ennek eredményeképpen a hideg test tovább hűl. Már csak azt kell kiszámítanunk, mennyire hűl le.

b) Először azt számítsuk ki, mennyi munka nyerhető a kezdetben T₁=90^oC=363 K és T₂=27 ^oC=300 K hőmérsékletű, m tömegű, c fajhőjű testek között működtetett hőerőgép segítségével! A legnagyobb munkát akkor nyerjük, ha egyensúlyi folyamatokat végző, úgynevezett reverzibilis Carnot-gépet használunk. Q₁-gyel, illetve Q₂-vel jelölve e körfolyamatot végző gép egyetlen ciklusában a T₁, illetve T₂ hőmérsékletű testektől felvett hőt, Q₁>0 és Q₂<0, ha T₁>T₂. Ekkor a ciklusonként végzett munka a termodinamika első főtétele szerint:

W=Q₁+Q₂.

Ugyanakkor a termodinamika második főtétele szerint

\(\displaystyle \frac{Q_{1}}{T_{1}}+\frac{Q_{2}}{T_{2}}=0\qquad\left(\eta=\frac{W}{Q_{1}}=\frac{T_{1}-T_{2}}{T_{1}}\right). \)

Egyetlen ciklus még alig változtatja meg a hőtartálynak tekinthető testek hőmérsékletét, elég sok ciklus után azonban egyre közelebb kerül egymáshoz a két test hőmérséklete.

Hogyan függ össze ez a két hőmérséklet? Helyettesítsük be a második főtételbe

\(\displaystyle Q_{1}=-c\,m\,\Delta T_{1}\qquad\text{\'es}\qquad Q_{2}=-c\,m\,\Delta T_{2} \)

értékeit (a negatív előjel azért kell, mert ami a munkavégző közeg szempontjából felvett hő, az a hőtartályok szempontjából leadott hőnek számít):

\(\displaystyle \frac{-c\,m\,\Delta T_{1}}{T_{1}}+\frac{-c\,m\,\Delta T_{2}}{T_{2}}=0. \)

Innen kapjuk, hogy

\(\displaystyle \frac{\Delta T_{1}}{T_{1}}+\frac{\Delta T_{2}}{T_{2}}=0,\)

T₂\(\displaystyle \Delta\)T₁+T₁\(\displaystyle \Delta\)T₂=\(\displaystyle \Delta\)(T₁T₂) =0,

vagyis

\(\displaystyle T_{1}T_{2}=\text{\'alland\'o.} \)

Tehát úgy változik a két test abszolút hőmérséklete, hogy a szorzatuk állandó marad! (Ez akkor és csak akkor van így, ha a két test hőkapacitása egyenlő; de ez most teljesül.) Végül is egy olyan közös hőmérséklet áll be, amelyre

\(\displaystyle T_{\text{k\''oz\''os}}^2=T_{1}T_{2}, \)

vagyis a közös hőmérséklet a kezdeti hőmérsékletek mértani közepe lesz. Esetünkben

\(\displaystyle T_{\text{k\''oz\''os}}=\sqrt{363~{\rm K}\cdot300~{\rm K}}=330~{\rm K}. \)

A melegebb test által leadott hő nagysága (a hőmérséklet kelvin mértékegységének kiírása nélkül):

c m^.(363-330)=c m^.33.

A hidegebb test által felvett hő nagysága:

c m^.(330-300)=c m^.30.

Így az összesen nyert munka: c m^.3, ezt használhatjuk fel majd a hűtőgép meghajtására.

Most már foglalkozhatunk a hűtőgéppel, aminek az alsó hőtartálya lesz a c fajhőjű, 2m tömegű, T₃=13 ^oC=286 K hőmérsékletű test. A felső hőtartály is c fajhőjű, és ugyancsak 2m tömegű, az előző folyamat végén nyert 330 K hőmérsékletű test. Ismét két azonos hőkapacitású testről van szó, vagyis most is állandó marad a két (abszolút) hőmérséklet szorzata.

Jelöljük T-vel az a kiszámítandó hőmérsékletet, amire a hideg test lehűl, és \(\displaystyle T^\star\)-gal azt a hőmérsékletet, amire a két másik test felmelegszik. Ekkor tehát

\(\displaystyle T\cdot T^\star=286\cdot330, \)

és az energiaegyenlet:

\(\displaystyle c\cdot2m(T^\star-330)-c\cdot2m(286-T)=c\,m\cdot3. \)

A fenti két egyenlet már meghatározza a keresett T és \(\displaystyle T^\star\) értékeket:

\(\displaystyle T=278~{\rm K}=5~{}^\circ{\rm C},\qquad T^\star=339{,}5~{\rm K}=66{,}5~{}^\circ{\rm C}. \)

Vagyis a kezdetben 13 ^oC-os test végül is 5 ^oC-osra hűthető le. Ezt kellett kiszámítanunk.

3. feladat. Egy fizikaszakkörön valaki demonstrálni szeretné, hogy ellentétes irányú elektromos térerősségvektorok leronthatják egymást. Elképzelése a következő. Szigetelő lábakon két egyforma fémgömböt állít egymás mellé és pontosan ugyanakkora potenciálra tölti fel őket. Ezután a kettejük közé középre belógatott próbatöltésre nem fog elektromos erő hatni.

A gyakorlati kivitelezéshez a kísérletező egy néhány száz V feszültségű telep egyik sarkát ,,leföldeli'', vagyis az asztallapra tett nagy fémtálcához csatlakoztatja - ezt tekinthetjük zérus potenciálú helynek -, a másik pólushoz csatlakozó banándugóval pedig először a bal oldali, utána a jobb oldali gömböt, majd végül a szigetelő szálon közéjük lógatott alufólia csíkot érinti meg (5. ábra). Meglepődve tapasztalja, hogy az alufólia igenis kitér a függőleges irányból, elmozdul az egyik gömb felé.

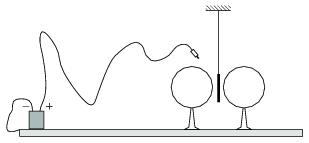
5. ábra

Mi lehet a kudarc magyarázata? (A levegő száraz, a lábak jól szigetelnek, a gömbök sokáig megtartják a rájuk vitt töltést.)

Melyik gömb felé tér ki az alufólia?

Hogyan lehetne a kudarcot elkerülni?

(Károlyházy Frigyes)

Megoldás. A feladat az 1992. évi Eötvös-verseny 3. problémájára emlékeztet, amelynek megoldása megtalálható ,,Az Eötvös-versenyek feladatai II. 1989-1997'' c. Typotex kiadványban, és ma már az interneten is olvasható a Kempelen Farkas Digitális Tankönyvtárban. Két versenyző, akik később dicséretet kaptak, rá is talált az ott közölt megoldásra, melynek nyomán sikerült is megoldaniuk ezt a feladatot. Az Eötvös-versenyen bármely segédeszköz (könyvek, jegyzetek, zsebszámológép) használható (mobiltelefon és laptop kivételével), ezért megoldásukat természetesen elfogadta a Versenybizottság. Most viszont szándékosan más megoldást közlünk, olyat, amilyet az idei verseny győztesei adtak erre a feladatra.

Tekintsük először azt az esetet, amikor még csak a bal oldali gömböt töltöttük fel a telep feszültségére. Ekkor ez a gömb felvett valamennyi töltést. A jobb oldali gömb, ami ugyan töltetlen, most egy elektromos erőtérbe került, ennek hatására benne töltésszétválás történt és már nem zérus a feszültsége, hiába zérus a rajta lévő össztöltés.

Ezek után érintjük meg a jobb oldali gömböt a telep előbbi - pozitív - sarkából jövő vezetékkel. Ennek hatására ez a gömb is a telep feszültségére töltődik fel, viszont ehhez már kevesebb töltésnek kell felmennie rá, mint amennyi töltés a másik gömbre került! Sőt, ha a második gömb feltöltése után megmérjük az első (a bal oldali) gömb feszültségét, az nagyobb lesz, mint a telep feszültsége, hiszen most már ez a gömb is erőtérbe, a jobb oldali gömb erőterébe került!

A helyzet annyira meglepő, hogy eredményhirdetéskor (technikai okokból egy 3000 V-os feszültségforrást használva) kísérletileg is bemutattuk. Amikor a bal oldali gömböt feltöltöttük 3000 V-ra, a jobb oldali gömbre kapcsolt elektrosztatikus voltmérő 800 V-ot mutatott. Amikor pedig a jobb oldali gömböt is feltöltöttük 3000 V-ra, a bal oldali gömb feszültsége 3800 V-ra nőtt!

Mindenképpen több töltés került tehát a bal oldali gömbre, mint a jobb oldalira, ezért a közéjük középre lógatott és feltöltött alufólia csíkra a bal oldali gömb nagyobb taszítóerőt gyakorol, mint a másik gömb. A fóliacsík tehát jobbra fog kilendülni!

Az egyik győztes versenyző (Almási Gábor) még azt is megjegyezte, hogy ha túl közel van egymáshoz a két gömb, akkor a közéjük lógatott fémfólián már töltetlen állapotban is a két gömb potenciálja közötti, tehát a telepfeszültségnél nagyobb potenciál alakulhat ki. Ezért, amikor hozzáérünk a telepből jövő vezetékkel, lehet, hogy leveszünk róla töltést, így áll be a fólia a telep feszültségére. Ebben az esetben azonban negatív töltése lesz, s a bal oldali gömb jobban fogja vonzani, mint a jobb oldali, vagyis ilyenkor a fólia balra lendül ki.

Hogyan lehetne elkerülni a kudarcot? Több mód is van rá. A legbiztosabb eljárás az, hogy egyszerre töltjük fel a két gömböt, de az is elég, ha kellő távolságra, viszonylag messze helyezzük őket egymástól. Igaz, ebben az esetben nem olyan látványos az a kísérlet, hogy közöttük középen nem hat erő a belógatott fóliára.

A verseny eredménye

Két versenyzőnek sikerült mindhárom feladatot hibátlanul megoldania, ezért két első díjat adott ki a Versenybizottság.

I. díj: Almási Gábor, az ELTE fizika BSc szakos hallgatója, aki a pécsi Leővey Klára Gimnáziumban érettségizett Simon Péter és Kotek László tanítványaként; és Szolnoki Lénárd, a BME fizika BSc szakos hallgatója, aki a Debreceni Református Kollégium Dóczy Gimnáziumában érettségizett Tófalusi Péter tanítványaként.

II. díj: Balogh Máté, a Fazekas Mihály Fővárosi Gyakorló Gimnázium 12. évf. tanulója, Horváth Gábor tanítványa; és Lovas Lia Izabella, a pécsi Leővey Klára Gimnázium 12. évf. tanulója, Simon Péter tanítványa.

III. díj: Farkas Márton, a Fazekas Mihály Fővárosi Gyakorló Gimnázium 12. évf. tanulója, Horváth Gábor tanítványa.

Dicséretet kaptak: Aczél Gergely, a Pápai Református Kollégium Gimnáziumának 12. évf. tanulója, Somosi István tanítványa; Iván Dávid, a fonyódi Mátyás Király Gimnázium 12. évf. tanulója, Németh László tanítványa; Karsa Anita, a Fazekas Mihály Fővárosi Gyakorló Gimnázium 12. évf. tanulója, Horváth Gábor tanítványa; Szilágyi Zsombor, az ELTE fizika BSc szakos hallgatója, aki a budapesti Karinthy Frigyes Gimnáziumban érettségizett Szilágyi László tanítványaként; és Wang Daqian, a Fazekas Mihály Fővárosi Gyakorló Gimnázium 11. évf. tanulója, Horváth Gábor tanítványa.

*

2008. november 21-én zajlott le az ünnepélyes eredményhirdetés. Először a Versenybizottság elnöke ismertette az 50, valamint a 25 évvel korábbi Eötvös-verseny feladatait, majd bemutatta az akkori díjazottak közül megjelent egykori versenyzőket.

Kovács Béla villamosmérnök, informatikus, aki 1958-ban érettségizett Sárospatakon, ma is gyakori látogatója egykori iskolájának. Őt is, mint az utána megszólaló, 25 évvel fiatalabb nyerteseket ez a verseny indította el életpályájukon. Árkossy Ottó orvos, Fodor Gyula és Frei Zsolt fizikusok lettek. Erdős László, aki Árkossy Ottóval holtversenyben lett első, matematikus lett. Jelenleg Münchenben dolgozik, onnan küldött üdvözletét Honyek Gyula olvasta fel.

A 25 évvel ezelőtt díjazott versenyzők mind a KöMaL sikeres megoldói voltak, az akkori fotóikból készített tabló nagy tetszést aratott. Meghívást kaptak az ünnepélyes eredményhirdetésre a díjazott és dicséretet kapott diákok tanárai, az Eötvös Loránd Fizikai Társulat minden tisztségviselője, valamint az Eötvös-versenyek nyertesei. Sokan eljöttek, néhányan levelet írtak, melyben üdvözölték az idei nyerteseket.

A díjakat és okleveleket Sólyom Jenő, az Eötvös Loránd Fizikai Társulat elnöke adta át. A két első díjas megkapta a Társulat Eötvös-verseny érmét és egyéves előfizetést a Fizikai Szemlére. Ezen kívül az első díjasok 20-20 ezer Ft, a második díjasok 15-15 ezer Ft, a harmadik díjas versenyző 10 ezer Ft, a dicséretes versenyzők pedig 5-5 ezer Ft pénzjutalomban részesültek, és mind a tízen megkapták Staar Gyula ,,Fizikusok az aranykorból'' c. könyvét.

A nyertes diákok megjelent tanárai a Vince és a Typotex kiadók által felajánlott könyvekből válogathattak.

A díjkiosztás után a Versenybizottság elnöke értékelte az idei versenyt, majd állófogadással egybekötött beszélgetésre invitálta a résztvevőket, megköszönve a Matfund Alapítvány, az Indotek Zrt., a Ramasoft Zrt. és Gutai László (USA) anyagi támogatását, amely nélkül nem lehetett volna megrendezni ezt az ünnepélyes eredményhirdetést és meleg kézszorításon kívül nem lehetett volna mással honorálni a versenyzők és tanáraik szép teljesítményét.

Ehhez csatlakozik a Versenybizottság is. Bízzunk a lendület megmaradásában ...