Kós Géza
Ismét egy egyszerű sejtautomatáról
avagy kutyák a Marsról
A játékot, amiről most szó lesz, Edward Fradkin találta ki, s már olvashattunk róla Marx György Szaporodás című írásában (KöMaL 1983/8-9. szám, 150-152. oldal). Mivel ez a cikk több mint tíz éve jelent meg, röviden leírjuk a sejtautomata működését.
Képzeljük el, hogy a világ a végtelen négyzethálós papír, melynek mezőin sejtek élnek, egy mezőn legfeljebb csak egy. Elhelyezkedésüket úgy ábrázoljuk, hogy befestjük azokat a négyzeteket, amelyek tartlamaznak sejtet. Szabályos időközönként minden sejt négyfelé osztódik, az utódok a négy élben szomszédos mezőre kerülnek. Ha több utód kerül egy mezőre, akkor párosával elpusztítják egymást, amíg legfeljebb csak egy marad. Ez azt jelenti, hogy a következő generációban akkor lesz sejt egy mezőn, ha az előző állapotban a négy szomszéd mező közül páratlan sok (1 vagy 3) tartalmazott sejtet.
Egy sejtből kiindulva, az első generációk így néznek ki:

1. ábra
Az alakzatoknak ezeket az átalakulásait kicsit másképp is elérhetjük. Tegyük fel, hogy egy mezőben több sejt is lehet, az egy mezőbe kerülő sejtek nem pusztítják el egymást. Azokat a négyzeteket, amelyekben páratlan sok sejt van, befestjük, a páros sok sejtet tartalmazó mezőket pedig fehéren hagyjuk. Könnyű végiggondolni, hogy a kapott alakzatok pontosan ugyanúgy néznek ki.
Az átfogalmazás nagyon hasznos: ha ugyanis a kiindulási alakzat több sejtből áll, és kiváncsiak vagyunk arra, hogy mi lesz n generáció múlva, akkor az utódokat kiszámíthatjuk minden egyes kiindulási sejtre, majd a kapott sejtszámokat minden egyes mezőben összeadjuk.
Mi történik az alakzatokkal a sejtszámok összeadásakor? Azok a mezők lesznek befestve, amelyek páratlan sok kiindulási sejt esetében lesznek n generáció múlva befestve. Ezt hívhatjuk az alakzatok egymásra szuperponálásának vagy összeadásának is. Az alábbi ábrán egy két sejtből álló alakzatra alkalmaztuk ezt az elvet. (Az egyik sejt leszármazottjait piros, a másik sejt utódait kék színnel jelöltük.)

2. ábra
Egy másik fontos tulajdonság, hogy egy sejtnek 2n lépés után négy utódja lesz, ezek az eredeti helyhez képest felfelé, lefelé, jobbra illetve balra helyezkednek el 2n távolságra. Ez például teljes indukcióval bizonyítható be. Ha n=0, akkor az állítás éppen az osztódási előírás. Ha pedig 2n lépés után négy utód van a megadott helyzetben, akkor újabb 2n lépés múlva ezek összesen 16 újabb utódot hoznak létre, amelyek közül csak négy marad meg, pontosan 2n+1 távolságra a négy megfelelő irányban.
Rakjunk össze néhány sejtből egy kisebb alakzatot, pl. kutyát. 2n generáció múlva a kutya minden sejtjének négy utódja keletkezik, amelyek az eredeti sejthez képest 2n távolságra lesznek felfelé, lefelé, jobbra illetve balra. Ezek az utódok összesen négy kutyává állnak össze. Ha az n kicsi, akkor a négy kutya "egymásba lóg" és a felismerhetetlenségig összezavarják egymást, "interferálnak". Ha viszont az n elég nagy, akkor a négy kutya nem lóg egymásba, hanem jól elkülönül. Ha az eltelt generációk száma nem pontosan kettőhatvány, de van egy elég nagy kettőhatvány osztója, akkor nem négy, hanem több kutyát láthatunk. Egy példa:

3. ábra
Számítógépes program I.
A játék számítógépes megvalósítása egy érdekes problémát vet fel. A számítógép ugyanis nem képes végtelen kockás papírt utánozni, hanem csak egy véges téglalapot. Ez azt is jelenti, hogy a képernyő szélén levő sejtek csak háromfelé osztódnak, a négy sarokban pedig csak kétfelé. Kérdés, hogy ez hogyan befolyásolja a végtelen papíron jól kezelhető és rendkívül látványos folyamatot.
Az alábbi Java applet egy lehetséges kiinduló állapot leszármazottait mutatja be.
A generációkat tanulmányozva érdekes jelenséget tapasztalunk: a végtelen papíron megszokott kutyákon kívül megjelennek különböző "tükörkép" kutyák is, amelyek bal helyett jobbra néznek, fejjel lefelé állnak vagy éppen fejjel lefelé állnak és jobbra néznek. Mintha a képernyő szélén "visszaverődnének" a kutyák.
A jelenség okát nyilván abban kell keresnünk, hogy a kép szélén levő sejtek osztódási szabálya más. Kevesebb felé osztódnak, a hiányzó utódok utódai hiányoznak a számunkra látható téglalapból. Mindenesetre ez még elég kevés magyarázat. A hiányzó utódok hányzó utódai hiányzó utódainak hatását elég nehéz nyomon követni, valamilyen más, átfogó módszert kell keresnünk.
A tükrözési elv
Hogy megértsük, mi is történik valójában a képernyő szélein, vizsgáljunk először egy egyszerűbb esetet. Legyen a világ egy félsík, határa legyen egy függőleges egyenes. Azt láttuk, hogy az osztódási szabályt nem változtathatjuk meg mesterségesen, mert egyelőre nem tudjuk a következményeket leírni. Éppen ezért úgy kell viselkednünk, mintha a világ az egész sík lenne, aminek csak a felét látjuk. Azok a sejtek, amelyek a látható világ szélén helyezkednek el, ugyanúgy négyfelé osztódnak, csak valamilyen, egyelőre nem ismert ok miatt a látható félsíkon kívülre kerülő utódaik azonnal elpusztulnak. Az ok természetesen a világ másik, nem látható felében keresendő. Miért ne lehetnének ott is sejtek, amelyeket ugyan nem látunk, de a hatásukat érzékeljük?
A feladat tehát az, hogy a világ nem látható részébe olyan sejteket helyezzünk el, amelyek utódai garantáltan mindig elpusztítják a látható világbeli sejteknek a nem látható részbe került utódait. Ezt nagyon egyszerűen megtehetjük. A látható félsík határán kijelölünk egy határsávot, amelyben nem lehet sejt. A határsáv másik oldalán pedig a látható világ tükörképét helyezzük el:
A sejtek elhelyezkedése mindig szimmetrikus lesz a határsávra, ezért a határsáv mezőibe csak párosával, mindkét oldalról egyszerre kerülhetnek sejtek, az ilyen sejtek elpusztítják egymást.
Mint az alábbi ábrán is láthatjuk, néhány generáció után a nem látható részben levő kutya sejtjeinek - kék színnel jelölt - utódai megjelennek a látható félsíkban:

Mindkét kutya a már látottaknak megfelelően négyfelé osztódott, de a nyolc utód kutyának csak a fele látható. A látható félsíkba került az eredeti kutyának három utódja, valamint a tükörkép kutya egyik utódja. A négy látható kutya közül tehát csak három származik az eredeti kutyától, a negyedik, a tükörkép "a túlvilágról jött".
Ha a világ téglalap alakú, akkor bonyolultabb a helyzet. A négy oldal mentén kijelölve egy-egy határsávot, a sík többi részén úgy kell sejteket elhelyeznünk, hogy a kapott alakzat mind a négy határsávra szimmetrikus legyen. Ezt úgy tehetjük meg, hogy a kiindulási téglalappal és a három tükörképével kicsempézzük a síkot az alábbi ábra szerint:
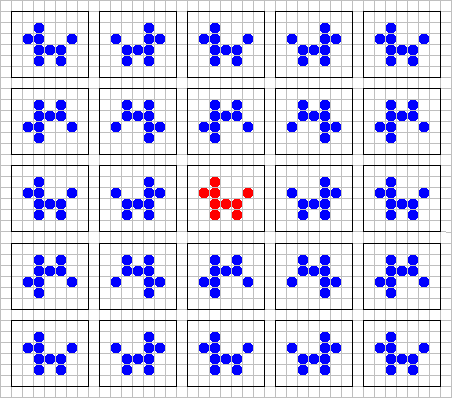
A különböző kutyák utódai időnként megjelennek abban a téglalapban is, amelyet látunk. Innen származnak a különféle tükörkép kutyák.
Feladatok
1. Mi történik akkor, ha a világ nem téglalap, hanem lépcsős, egyenlő szárú, derékszögű háromszög?
2. Mi a helyzet akkor, ha a sejtek kilencfelé osztódnak, egy utód az eredeti helyen marad, a többi nyolc a csúcsban szomszédos mezőkre kerül?
3. Tegyük fel, hogy minden sejt n-felé osztódik, az utódok helyére az eredeti helyről a v1 v2, ..., vn vektorok mutatnak. Bizonyítsuk be, hogy két lépés után is n utód keletkezik, ezek helyére a 2v1 2v2, ..., 2vn vektorok mutatnak.
4. Legyen a világ egy kxn méretű téglalap. Bizonyítsuk be, hogy ha k+1 és n+1 kettőhatvány, akkor bármilyen alakzatból indulunk ki, az előbb-utóbb kipusztul!
5. Mi történik akkor, ha a sejtek nem kettesével, hanem hármasával pusztítják el egymást? Hogyan változik akkor a 3. feladat állítása? Hogyan módosul a tükrözési elv?
6. Legyen a világ egy kxn méretű téglalap, és tegyük fel, hogy bármilyen alakzatból indulunk is ki, az előbb-utóbb kipusztul. Bizonyítsuk be, hogy vagy k+1 és n+1 is kettőhatvány, vagy pedig n=k=2.
Számítógépes program II.
A következő Java applettel több különböző érdekes helyzetet tanulmányozhatunk, és az előbbi feladatok válaszait is demonstrálhatjuk. Javasoljuk, hogy a kedves Olvasó csak a feladatok megoldása után próbálja ki a programot.
Az osztódási folyamatot a Start és Stop gombokkal indíthatjuk el és állíthatjuk le. Amikor a folyamat áll, kiválaszthatjuk az osztódási szabályt és előírhatjuk, hogy a sejtek kettesével (modulo 2) vagy hármasával (modulo 3) pusztítsák el egymást. Ezen kívül a megfelelő mezőkre klikkelve beállíthatunk egy új kiinduló sejthalmazt.
Lehetőség van tiltott mezők kijelölésére is, az ezekre kerülő sejtek elpusztulnak. A tiltott mezők elhelyezésével megváltoztathatjuk a tábla méretét és alakját.

