Kiss György

Amit jó tudni a háromszögekről

A lapunkban megjelenő feladatok mintamegoldásainak írása közben sokszor jelent problémát annak eldöntése, hogy egy állítás közismert-e, s ezért nem kell bizonyítani, vagy pedig nem az, és ezért a bizonyítását is le kell írni. Különösen így volt ez a B. 3478. feladatnál, amit nagyon sokféleképpen lehetett megoldani.

E cikknek az a célja, hogy a háromszögekkel kapcsolatos néhány állítás egyszerű bizonyításait összegyűjtse. A háromszögekkel kapcsolatban rengeteg tétel van, mi csak azokkal foglalkozunk, amelyek kapcsolódnak a háromszöghöz tartozó körökhöz. Ezeknek is csak egy részét ismertetjük, egyáltalán nem foglalkozunk pl. a Feuerbach körrel. Az érdeklődő olvasó további szép tételeket találhat az irodalomjegyzékben szereplő könyvekben.

A háromszögben a három oldal, csúcs, szög stb. szerepe szimmetrikus. Ezért állításainkban és bizonyításainkban a rövidség kedvéért sokszor csak a,A,$\displaystyle alpha$,... szerepel. Ezeket persze úgy kell érteni, hogy a háromszög tetszőleges oldalára, csúcsára, szögére igaz a megfelelő állítás.

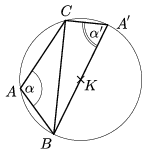
Legyenek a háromszög csúcsai A, B, C, oldalai a, b, c, szögei $\displaystyle alpha$, $\displaystyle beta$, $\displaystyle gamma$, a szokásos jelölésekkel a háromszög területét jelölje T, kerületét 2s, a beírható kör sugara legyen r, a hozzáírt körök sugarai r_a, r_b, r_c, a háromszög köré írható kör sugara R, végül ezen körök középpontjai legyenek rendre O, O_a, O_b, O_c és K (1. ábra).

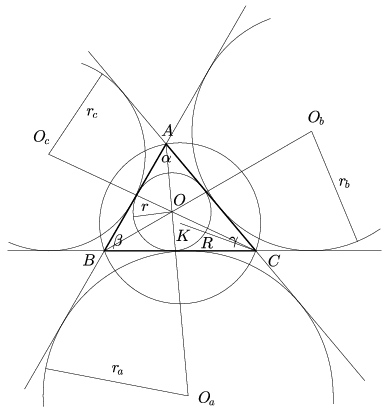
1. ábra

Első állításunkat általánosított szinusztételnek is szokás nevezni.

1. állítás. $\displaystyle R=\frac a{2\sin\alpha}=\frac b{2\sin\beta}=\frac c{2\sin\gamma}$.

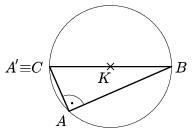
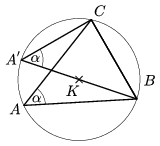
Bizonyítás. Messe a háromszög köré írható körének BK átmérője a kört másodszor az A' pontban. Ekkor BA'=2R. Ha $\displaystyle alpha$=90^o, akkor A' $equiv$ C, az állítás nyilvánvaló ( 2/1. ábra). Ha $alpha$ nem derékszög, akkor BA'C$\displaystyle angle$=$\displaystyle alpha$ (2/2. ábra), vagy BA'C $angle$ = $alpha$ '=180^o-$\displaystyle alpha$ ( 2/3. 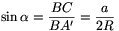ábra), de felhasználva a sin (180^o-$\displaystyle alpha$)=sin$\displaystyle alpha$ összefüggést, valamint azt, hogy a BA'C háromszög C-nél lévő szöge Thalész tétele miatt derékszög, mindig teljesül, hogy $\sin\alpha=\frac{BC}{BA'}=\frac{a}{2R}$ .


2/1. ábra	2/2. ábra	2/3. ábra

2. állítás. $\displaystyle R=\frac{abc}{4T}$.

Bizonyítás. Az ismert területképlet szerint 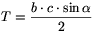$T=\frac{b\cdot c\cdot\sin\alpha}{2}$ . Ezért ha az előző állításban belátott 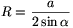$R=\frac{a}{2\sin\alpha}$ összefüggés jobb oldalán lévő törtet b^.c-vel bővítjük, akkor éppen a bizonyítandó összefüggést kapjuk.

Ha a $\displaystyle T=\frac{b\cdot c\cdot\sin\alpha}{2}$ területképletben az oldalakat kifejezzük az 1. állításból adódó 2Rsin $beta$ -val, illetve 2Rsin$\displaystyle gamma$-val, akkor a következőt kapjuk:

3. állítás. T=2R²sin $alpha$ sin $beta$ sin $gamma$ .

Tudjuk, hogy O a háromszög három belső szögfelezőjének, O_a, O_b és O_c pedig két-két külső- és egy-egy belső szögfelezőjének a metszéspontja. Mivel a háromszög bármely csúcsához tartozó külső és belső szögfelező merőleges egymásra, ezért igaz a következő:

4. állítás. Az O_aO_bO_c háromszög magasságpontja O, magasságvonalai pedig megegyeznek az ABC háromszög belső szögfelezőivel.

Ebből következik, hogy az OBO_aC négyszög húrnégyszög, mert B-nél és C-nél lévő szögei egyaránt derékszögek. A négyszöget az OO_a átló két közös átfogójú derékszögű háromszögre bontja, ezért a négyszög köré írható kör középpontja az OO_a szakasz felezőpontja. A négyszög köré írt kört megrajzolva (3. ábra) látszik, hogy OCB$\displaystyle angle$=OO_aB $angle$ és OBC$\displaystyle angle$=OO_aC $angle$ , mert az egy íven nyugvó kerületi szögek egyenlőek. 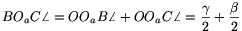Vagyis $BO_aC\angle=OO_aB\angle+OO_aC\angle=\frac{\gamma}{2}+\frac{\beta}{2}$ . Ezzel bebizonyítottuk a következőt:

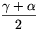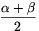5. állítás. Az O_aO_bO_c háromszög szögei rendre: $\displaystyle \frac{\beta+\gamma}{2}$, $\frac{\gamma+\alpha}{2}$ és $\frac{\alpha+\beta}{2}$ .


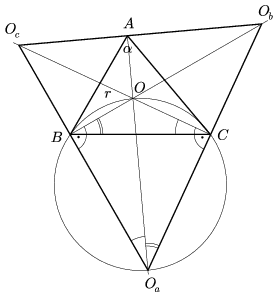3. ábra	4. ábra

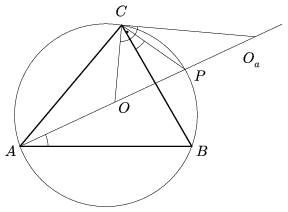
Következő állításunk az eddigieknél kevésbé ismert (bár megtalálható a Geometriai feladatok gyűjteménye I. kötetében).

6. állítás. A háromszög köré írható kör felezi a beírható kör középpontját a hozzáírható körök középpontjaival összekötő szakaszokat.

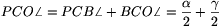Bizonyítás. Messe a köré írható kör az OO_a szakaszt P-ben (4. ábra). (Mivel $\displaystyle CO_aB\angle=\frac{\beta+\gamma}{2}<180^\circ\!-\alpha=180^\circ\!-CAB\angle$, ezért O_a a köré írható körön kívül helyezkedik el, vagyis P mindig létrejön.) Ekkor PCB $angle$ =PAB $angle$ , mert mindkettő a PB ívhez tartozó kerületi szög. Ezért $PCO\angle=PCB\angle+BCO\angle=\frac{\alpha}{2}+\frac{\gamma}{2}$ . 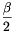Az OCO_a háromszögben C-nél derékszög van, az O_a-nál lévő szögről már láttuk, hogy $\frac{\beta}{2}$ , ezért az O-nál lévő szög $\displaystyle 90^\circ\!-\frac{\beta}{2}=\frac{\alpha}2+\frac{\gamma}{2}$. Vagyis POC$\displaystyle angle$=PCO$\displaystyle angle$, tehát a POC háromszög egyenlő szárú, PO=PC. Ugyanígy láthatjuk be, hogy PO=PB. Ez azt jelenti, hogy az OBC háromszög köré írható kör középpontja P. Ez a kör azonban megegyezik az OBO_aC húrnégyszög köré írható körrel, hiszen mindkét sokszögnek csúcsa O, B és C. Azt viszont a 4. állítás után beláttuk, hogy az OBO_aC köré írható kör középpontja az OO_a szakasz felezőpontja. Tehát P felezi OO_a-t.

7. állítás. A hozzáírt körök középpontjai által meghatározott háromszög köré írható körének sugara 2R.

Bizonyítás. Ha az O pontból kétszeresére nagyítjuk a köré írható kört, akkor a keletkezett 2R sugarú kör az 5. állítás miatt átmegy az O_a, O_b és O_c pontok mindegyikén (5. ábra).

5. ábra

(A 6. és 7. állításokat a fentieknél egyszerűbben beláthatja az, aki ismeri a Feuerbach-kör tulajdonságait -- lásd pl. [2], 69--70. oldal --, a 3. állításból ugyanis következik, hogy az O_aO_bO_c háromszög Feuerbach-köre megegyezik az ABC háromszög körülírt körével. Ebből pedig nemcsak 6. és 7. következik, hanem az is, hogy a körülírt kör felezi a hozzáírt körök középpontjai által meghatározott szakaszokat.)

A továbbiakban a beírt és a hozzáírt körök sugarait fejezzük ki az oldalakkal és a területtel. Ehhez először meghatározzuk ezen körök és az oldalegyenesek érintési pontjainak a háromszög csúcsaitól való távolságát. Jelöljük az érintési pontokat a 6. ábrán látható módon D, E, F, G, H, I-vel. Mivel egy külső pontból egy körhöz húzott két érintőszakasz hossza egyenlő, ezért AH=AI, BG=BI és CH=CG, továbbá a 6. ábra jelöléseinek megfelelően AE=AF=x, BD=BF=y és CD=CE=z.

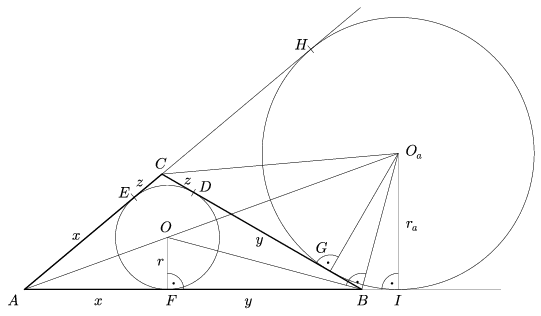
6. ábra

Az x+y=c, y+z=a és z+x=b összefüggésekből következik, hogy 2x+2y+2z=a+b+c=2s, azaz x+y+z=s, és így

(1)	x=s-a, y=s-b, z=s-c.

A hozzáírt körhöz húzott érintőszakaszokra pedig

2AH=AH+AI=(AC+CG)+(AB+BG)=AC+AB+BC=2s,

tehát

(2)	AH=AI=s, BG=BI=s-c, CH=CG=s-b.

8. állítás. T=r^.s=r_a(s-a)=r_b(s-b)=r_c(s-c).

Bizonyítás. Az ABC háromszög területe megegyezik az OAB, OBC és OCA háromszögek területének összegével. E három háromszög O-hoz tartozó magasságai r hosszúak, így területeik rendre 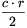$\frac{c\cdot r}{2}$ , $\displaystyle \frac{a\cdot r}{2}$ és $\displaystyle \frac{b\cdot r}{2}$. Ezeket összeadva kapjuk, hogy T=r^.s.

A hozzáírt kör esetén azt kell felhasználnunk, hogy az ABC háromszög területe megegyezik az O_aAB és O_aCA háromszögek területei összegének és az O_aBC háromszög területének különbségével, azaz

$\displaystyle T=\frac{c\cdot r_a}{2}+\frac{b\cdot r_a}{2}-\frac{a\cdot r_a}{2}=r_a(s-a).$

9. állítás. A beírt kör sugarának reciproka megegyezik a hozzáírt körök sugarának reciprokösszegével.

Bizonyítás. A 8. állítás szerint

$\displaystyle \frac{1}{r_a}+\frac{1}{r_b}+\frac{1}{r_c}=\frac{s-a}{T}+\frac{s-b}{T}+\frac{s-c}{T}=\frac{3s-(a+b+c)}{T}=\frac{s}{T}=\frac{1}{r}.$

10. állítás (Héron képlete). 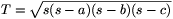$T=\sqrt{s(s-a)(s-b)(s-c)}$ .

Bizonyítás. A 6. ábrán látható OBF és BO_aI háromszögek hasonlóak, mert F-nél illetve I-nél derékszögük van, a külső és a belső szögfelezők merőlegessége miatt pedig OBF $angle$ és BO_aI $angle$ merőleges szárú hegyesszögek. Ezért a két háromszög megfelelő oldalainak aránya megegyezik:

$\displaystyle \frac{OF}{FB}=\frac{BI}{IO_a}.$

Ezt (1), (2) és a 8. állítás felhasználásával átalakítva:

$\displaystyle \frac{r}{s-b}=\frac{s-c}{r_a},$ azaz 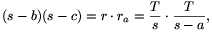$(s-b)(s-c)=r\cdot r_a=\frac{T}{s}\cdot\frac{T}{s-a},$

amiből T²=s(s-a)(s-b)(s-c) adódik.

11. állítás. 4R=r_a+r_b+r_c-r.

Bizonyítás. A 2. és a 8. állítás alapján elegendő azt megmutatnunk, hogy

(3)	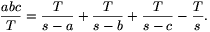$\frac{abc}{T}=\frac{T}{s-a}+\frac{T}{s-b}+\frac{T}{s-c}-\frac{T}{s}.$

Mindkét oldalt T-vel szorozva és felhasználva Héron képletét:

(4)	abc=s(s-b)(s-c)+s(s-a)(s-c)+s(s-a)(s-b)-(s-a)(s-b)(s-c).

Ez az egyenlőség a jobb oldal átalakításával könnyen belátható:

[s-(s-a)](s-b)(s-c)+s(s-a)[(s-c)+(s-b)]=

$\displaystyle =a\cdot\frac{1}{4}\big(a^2-{(b-c)}^2\big)+\frac{1}{4}\big({(b+c)}^2-a^2\big)\cdot a=\frac{1}{4}a\cdot4bc=abc.$

Vagyis (4), s így a vele ekvivalens (3) is igaz.

12. állítás. A háromszög köré írható kör sugara legalább kétszerese a beírható kör sugarának.

Bizonyítás. Azt kell megmutatnunk, hogy R $ge$ 2r, vagyis a 2. és 8. állításokat felhasználva azt, hogy

(5)	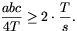$\frac{abc}{4T}\ge2\cdot\frac{T}{s}.$

Szorozzuk meg mindkét oldalt T/2-vel, alkalmazzuk Héron képletét és egyszerűsítsünk a jobb oldalon s-sel:

$\displaystyle \frac{abc}{8}\ge(s-a)(s-b)(s-c).$

Írjuk át a bizonyítandó egyenlőtlenséget az (1) összefüggéseket felhasználva az x, y, z változókra:

$\displaystyle \frac{(y+z)(z+x)(x+y)}{8}\ge x\cdot y\cdot z.$

Ez viszont azonnal adódik a számtani és mértani közepek közti

$\displaystyle \frac{y+z}{2}\ge\sqrt{yz},\quad\frac{z+x}{2}\ge\sqrt{zx}$ és $\displaystyle \frac{x+y}{2}\ge\sqrt{xy}$

egyenlőtlenségek összeszorzásából. Ezért az ezzel ekvivalens (5) egyenlőtlenség is teljesül. Az is látható, hogy egyenlőség csak akkor van, ha x=y=z, azaz ha a háromszög szabályos.

Héron képletét valamint a számtani és a mértani közepek közti egyenlőtlenséget felhasználva kapjuk, hogy

(6)	$\displaystyle T^2=s(s-a)(s-b)(s-c)\le s\left(\frac{(s-a)+(s-b)+(s-c)}{3}\right)^3=s\cdot\frac{s^3}{27}=\frac{s^4}{27}.$

Vagyis minden háromszögben igaz, hogy $\displaystyle 12\sqrt{3}\le\frac{{(2s)}^2}{T}$, azaz a kerület négyzetének és a területnek a hányadosa alulról korlátos. Ez a tört minimális értékét akkor veszi fel, ha (6)-ban egyenlőség van, tehát amikor a háromszög szabályos. Ebből azonnal adódik a következő két, szélsőértékekre vonatkozó állítás.

13. állítás. Adott területű háromszögek közül a szabályosnak a legkisebb a kerülete.

14. állítás. Adott kerületű háromszögek közül a szabályosnak a legnagyobb a területe.

A továbbiakban a háromszög szögeinek és félszögeinek szögfüggvényeit fejezzük ki az oldalakkal majd ezeknek a képleteknek néhány alkalmazását mutatjuk meg.

15. állítás.

$\displaystyle \tg\frac{\alpha}{2}=\sqrt{\frac{(s-b)(s-c)}{s(s-a)}},$

$\displaystyle \tg\frac{\beta}{2}=\sqrt{\frac{(s-a)(s-c)}{s(s-b)}}$

és

$\displaystyle \tg\frac{\gamma}{2}=\sqrt{\frac{(s-a)(s-b)}{s(s-c)}}.$

Bizonyítás. A 6. ábrán látható AFO derékszögű háromszög A-nál lévő szöge $\displaystyle \frac{\alpha}{2}$. Ezért a 8. állítást, Héron képletét és (1)-et felhasználva:

$\displaystyle \tg\frac{\alpha}{2}=\frac{OF}{AF}=\frac{r}{x}=\frac{T}{sx}=\frac{\sqrt{s(s-a)(s-b)(s-c)}}{s(s-a)}=\sqrt{\frac{(s-b)(s-c)}{s(s-a)}}.$

Az AFO háromszögben Pitagorasz tétele szerint

$\displaystyle AO^2=AF^2+OF^2={(s-a)}^2+\frac{T^2}{s^2}=\frac{s-a}{s}\big[s(s-a)+(s-b)(s-c)\big]=$

$\displaystyle =\frac{s-a}{4s}\Big[\big({(b+c)}^2-a^2\big)+\big(a^2-{(b-c)}^2\big)\Big]=bc\frac{s-a}{s}.$

Ennek ismeretében a tangenshez hasonlóan kifejezhetjük $\displaystyle \frac{\alpha}{2}$ szinuszát és koszinuszát is:

(7)	$\displaystyle \sin\frac{\alpha}{2}=\frac{OF}{AO}=\frac{T}{s\cdot AO}=\frac{\sqrt{s(s-a)(s-b)(s-c)}}{s\cdot\sqrt{bc\displaystyle\frac{\strut s-a}{s}}}=\sqrt{\frac{(s-b)(s-c)}{bc}}$

(8)	$\displaystyle \cos\frac{\alpha}{2}=\frac{AF}{AO}=\frac{s-a}{\sqrt{bc\displaystyle\frac{\strut s-a}{s}}}=\sqrt{\frac{s(s-a)}{bc}}.$

Ezekből a $\displaystyle \sin\alpha=2\sin\frac{\alpha}{2}\cos\frac{\alpha}{2}$ és a $\displaystyle \cos\alpha=\cos^2\frac{\alpha}{2}-\sin^2\frac{\alpha}{2}$ trigonometrikus azonosságokat felhasználva kapjuk, hogy

$\displaystyle \sin\alpha=2\sqrt{\frac{(s-b)(s-c)}{bc}}\sqrt{\frac{s(s-a)}{bc}}=\frac{2T}{bc},$

ami az ismert területképlet átrendezett alakja, valamint hogy

$\displaystyle \cos\alpha=\frac{s(s-a)}{bc}-\frac{(s-b)(s-c)}{bc}=\frac{1}{4bc}\Big[\big({(b+c)}^2-a^2\big)-\big(a^2-{(b-c)}^2\big)\Big]=$

$\displaystyle =\frac{b^2+c^2-a^2}{2bc},$

ami a koszinusztétel egy átrendezett alakja.

A tangenseket (feltéve, hogy a szög nem derékszög), a $\displaystyle \tg\varphi=\frac{\sin\varphi}{\cos\varphi}$ azonosság alapján kifejezve egy kevésbé ismert összefüggést kapunk:

(9)	4T=tg$\displaystyle alpha$(b²+c²-a²)=tg$\displaystyle beta$(a²+c²-b²)=tg$\displaystyle gamma$(a²+b²-c²).

Ebből azonnal adódik, hogy

$\displaystyle \ctg\alpha+\ctg\beta+\ctg\gamma=\frac{b^2+c^2-a^2}{4T}+\frac{a^2+c^2-b^2}{4T}+\frac{a^2+b^2-c^2}{4T}=\frac{a^2+b^2+c^2}{4T}.$

Következő állításunk már nem ilyen nyilvánvaló.

16. állítás. Ha a háromszög nem derékszögű, akkor

tg$\displaystyle alpha$+tg$\displaystyle beta$+tg$\displaystyle gamma$=tg$\displaystyle alpha$^.tg$\displaystyle beta$^.tg$\displaystyle gamma$.

Bizonyítás. Felhasználva (9)-et, azt kell megmutatnunk, hogy

$\displaystyle \frac{4T}{b^2+c^2-a^2}+\frac{4T}{a^2-b^2+c^2}+\frac{4T}{a^2+b^2-c^2}=$

$\displaystyle =\frac{64T^3}{(b^2+c^2-a^2)(a^2+c^2-b^2)(a^2+b^2-c^2)}.$

Ha a háromszög nem derékszögű, akkor ez ekvivalens a nevezőkkel való szorzás és 4T-vel való osztás után kapott

(a²+b²-c²)(a²+c²-b²)+(a²+b²-c²)(b²+c²-a²)+(b²+c²-a²)(a²+c²-b²)=16T²

összefüggéssel. A jobb oldalra beírva Héron képletét és mindkét oldalt rendezve:

(a²+b²-c²)^.2c²+(b²+c²-a²)(a²+c²-b²)=[(b+c)²-a²][a²-(b-c)²].

Átalakítva:

2c²[(a²+b²-c²)+(b²+c²-a²)]+(b²+c²-a²)(a²-b²-c²)=

=(b²+c²-a²+2bc)(a²-b²-c²+2bc),

4b²c²+(b²+c²-a²)(a²-b²-c²)=

(b²+c²-a²)(a²-b²-c²)+2bc[(b²+c²-a²)+(a²-b²-c²)]+4b²c².

Ez az azonosság bizonyítja állításunkat.

A 15. állítást, a (7) és (8) képleteket (és megfelelőiket $\displaystyle \frac{\beta}{2}$ és $\displaystyle \frac{\gamma}{2}$ szögfüggvényeire) valamint Héron képletét felhasználva triviális számolással kapjuk a következő azonosságokat.

17. állítás.

$\displaystyle \tg\frac{\alpha}{2}\cdot\tg\frac{\beta}{2}\cdot\tg\frac{\gamma}{2}=\frac{T}{s^2},$

$\displaystyle \ctg\frac{\alpha}{2}\cdot\ctg\frac{\beta}{2}\cdot\ctg\frac{\gamma}{2}=\frac{s^2}{T},$

$\displaystyle \sin\frac{\alpha}{2}\cdot\sin\frac{\beta}{2}\cdot\sin\frac{\gamma}{2}=\frac{T^2}{s\cdot abc},$

$\displaystyle \cos\frac{\alpha}{2}\cdot\cos\frac{\beta}{2}\cdot\cos\frac{\gamma}{2}=\frac{s\cdot T}{abc}.$

Ezeket felhasználva sok egyenlőtlenség könnyen belátható, ezek közül egyet mutatunk meg példaként.

18. állítás. $\displaystyle \sin\frac{\alpha}{2}\cdot\sin\frac{\beta}{2}\cdot\sin\frac{\gamma}{2}\le\frac{1}{8}$.

Bizonyítás. A 17. állítás alapján elegendő belátnunk, hogy

$\displaystyle \frac{T^2}{s\cdot abc}\le\frac{1}{8},$ azaz $\displaystyle \frac{T^2}{s}\le\frac{abc}{8}.$

Héron képletét felhasználva ez $\displaystyle (s-a)(s-b)(s-c)\le\frac{abc}{8}$ alakba is írható. Ezt az egyenlőtlenséget viszont már beláttuk a 12. állítás bizonyítása során.

Irodalom

[1] Coxeter, H. S. M.: A geometriák alapjai, Műszaki Könyvkiadó, Budapest, 1987.

[2] Reiman I.: A geometria és határterületei, Gondolat Könyvkiadó, Budapest, 1986.

Már regisztráltál?
Új vendég vagy?