Számadó László
Statisztika a 9. osztályban
A feladatok megoldása
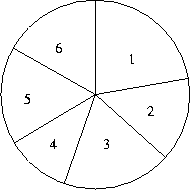
1. A következő táblázatot kaptam:
|
Oszlopdiagramon ábrázolva:
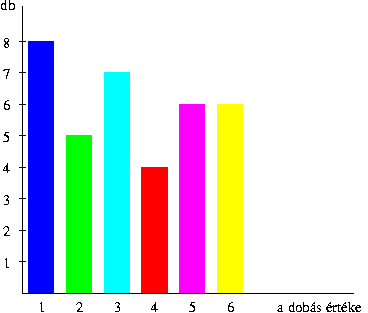
Kördiagramon ábrázolva:
2. A következő táblázatot kaptam:
|
Oszlopdiagramon ábrázolva:
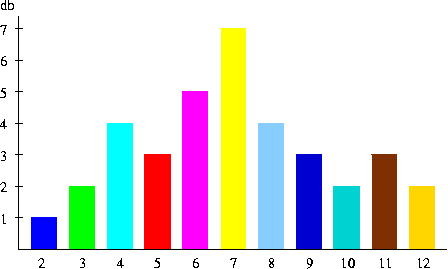
Kördiagramon ábrázolva:
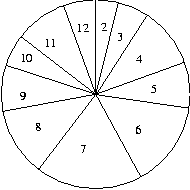
3.
|
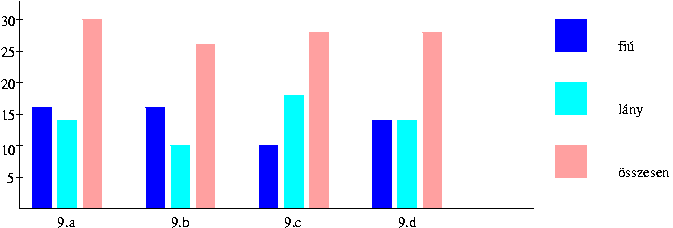
4. Négyzetlapok segítségével a következő ábra készíthető:
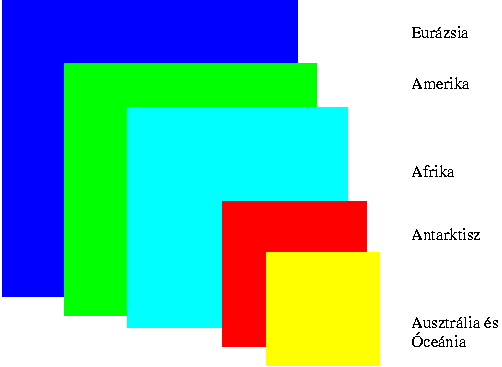
5. A napilapokból, folyóiratokból gyűjtött grafikonokról, táblázatokból főleg az adatok nagyságrendjét, az egymáshoz való viszonyukat próbáljuk leolvasni.
6. A gyakorisági eloszlás egy-egy osztályra lesz jellemző. Például egy 32 fős osztályban lehet a következő:
|
Ha egy cipőboltban az osztály minden tanulója vásárolt 1 pár cipőt, akkor 41-es méretből 8 darabot fognak vásárolni, ekkor ez a méret fogy a legjobban. Ez a tanult középértékek közül a módusz.
7. Megnéztünk 31 személygépkocsit, a következő gyakorisági eloszlást kaptuk:
|
A számsokaság átlaga 1,8.
Így számoltunk: (1.17+2.7+3.4+4.2+5.1)/31\(\displaystyle approx\)1,8.
A számsokaság módusza 1, hiszen a gyakorisági táblázatban jól látható, hogy az 1 szerepel a leggyakrabban.
A számsokaság mediánja 1, mert az adatok nagyságszerinti rendezésekor a 16. helyen, vagyis középen 1 áll.
Ezek alapján elmondható, hogy a személygépkocsik kihasználtsága nagyon alacsony. Látható, hogy az átlag 1,8. Azonban 1,8 utas nem lehet a személygépkocsiban, ezért kerekíthetnénk 2-re; de ez nem mutatná azt, amit a felmérésnél tapasztaltunk: hogy szinte minden második autóban csak a vezető ül.
Természetesen itt jól érvényesül az adatgyűjtés mikéntje is. Nem mindegy, hogy a nap melyik szakában, milyen helyen végezzük az adatok gyűjtését. A "mikor" és a "hol" ismerete nélkül csak nagyon óvatos vélemény fogalmazható meg az adatok alapján. Nagyon jól megfigyelhető az adatok számának fontossága is. Ha biztonságosabb elemzést, véleményt szeretnénk megfogalmazni, akkor nagyobb mintát kell gyűjtenünk.
8. Megkönnyíti a munkánkat, ha elkészítjük a gyakorisági táblázatot:
|
A számsokaság módusza 23, hiszen a gyakorisági táblázatban jól látható, hogy a 23 szerepel a leggyakrabban (ez az adat hatszor fordul elő).
A számsokaság mediánja 24,5, mert az adatok nagyságszerinti rendezésekor a 15. helyen 24, a 16. helyen 25 áll, így ezek számtani közepét kellett vennünk.
A 30 évszám összege 775, így számsokaság átlaga 775/30\(\displaystyle approx\)25,8.
A következő kérdéseket fogalmazhatjuk meg.
Kérdés, amelyre a módusszal válaszolunk: "A megkérdezettek alapján melyik a "legnépszerűbb" életkor az első szülésre?"
Kérdés, amelyre a mediánnal válaszolunk: "Hány évesen szülte első gyermekét az a nő, aki elmondhatja magáról, hogy kb. ugyanannyian később és ugyanannyian korábban szülték első gyermeküket, mint ő?"
Kérdés, amelyre az átlaggal válaszolunk: "Mennyi a számsokaság átlaga?" (Ha valakinek "ötletesebb" kérdés is eszébe jut, az nagyon jó!)
9. Az átlag nem mond sokat. Gondoljuk meg, hogy ha a cég vezetője nagyon sokat keres, az alkalmazottak pedig nagyon keveset, akkor az átlag egy olyan szám lesz, ami ilyen szempontból nem ad igazán hasznos információt. Érdemes a mediánt, vagy a móduszt megkérdezni.
10. Mivel a 16 lány a testmagasságának átlaga 168 cm, ezért a lányok testmagasságának
összege
16.168=2688 cm.
Mivel a 14 fiú testmagasságának átlaga 174 cm, ezért a fiúk testmagasságának összege
14.174=2436 cm.
Az osztály testmagasságának összege
2688+2436=5124 cm.
Az osztály testmagasságának átlaga
5124/30=170,8 cm.
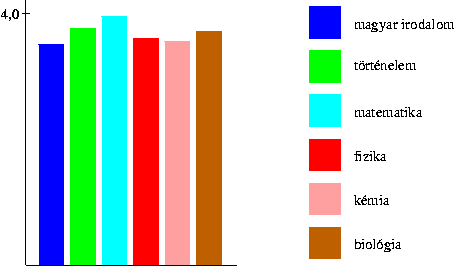
11. a) A következő oszlopdiagrammal megmutatható szülői értekezleten, hogy a tanulók a különböző tantárgyakban viszonylag egyenletesen teljesítenek. Az oszlopok magasságai között nincs nagy eltérés.
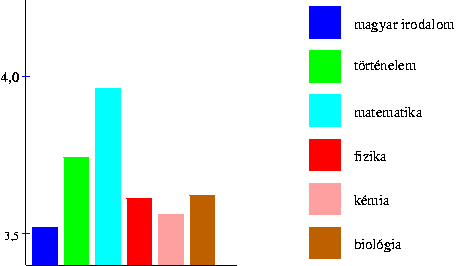
b) A következő oszlopdiagrammal megmutatható az iskola igazgatójának, hogy a tanulók matematikából kiugróan jók a többi tantárgyhoz képest. Mivel minden eredmény 3,5 és 4,0 között van, ezért ezt a részt emeltük ki erősebben, az oszlopokat nem rajzoltuk meg teljesen. Így elértük a kívánt hatás: az egyik oszlop (a matematikához tartozó) lényegesen magasabbnak tűnik.
12. a) A három tanulót jelölje A, B és C, a három tantárgyat x, y és z. A megfelelő félévi jegyet (a, b, c, d, e, f, g, h, i) a következő táblázatból megtudhatjuk.
|
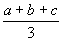 ,
a B tanuló átlaga
,
a B tanuló átlaga 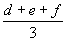 ,
a C tanuló átlaga
,
a C tanuló átlaga 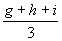 .
.
A tanulók átlagainak az átlaga 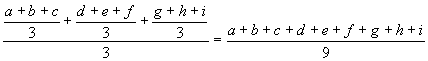 .
.
Az x tantárgy átlaga 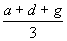 ,
az y tantárgy átlaga
,
az y tantárgy átlaga 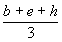 ,
a z tantárgy átlaga
,
a z tantárgy átlaga 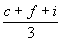 .
.
A tantárgyak átlagainak az átlaga 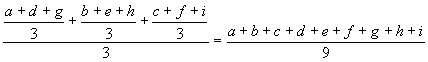 .
.
Láthatjuk, hogy a tanulók átlagainak az átlaga és a tantárgyak átlagainak az átlaga egyenlő.
b) Az n tanulót jelölje A1,A2,...,An, a k tantárgyat x1,x2,...,xk. A megfelelő félévi jegyet (a1;1,a1;2,...,a1;k,a2;1,...,an;k) a következő táblázatból megtudhatjuk.
|
Az A1 tanuló átlaga 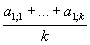 ,
az A2 tanuló átlaga
,
az A2 tanuló átlaga 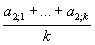 , ..., az An tanuló átlaga
, ..., az An tanuló átlaga 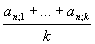 .
.
A tanulók átlagainak az átlaga 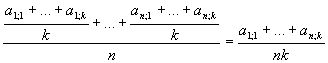 .
.
Az x1 tantárgy átlaga 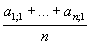 ,
az x2 tantárgy átlaga
,
az x2 tantárgy átlaga 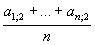 , ..., az xk tantárgy átlaga:
, ..., az xk tantárgy átlaga: 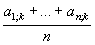 .
.
A tantárgyak átlagainak az átlaga 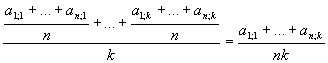 .
.
Láthatjuk, hogy a tanulók átlagainak az átlaga és a tantárgyak átlagainak az átlaga egyenlő.
13. A következő táblázat tartalmazza az ismert átlagokat. A két osztályban az összes lány átlagpontszámát jelölje x.
|
A 9. A osztályban a fiú, a 9. B osztályban b fiú, a 9. A osztályban c lány, a 9. B osztályban d lány van.
A táblázat első sora alapján a következő egyenletet írhatjuk fel:
40,5.a+45.c=42.(a+c).
A táblázat második sora alapján pedig a következőt:
35,5.b+38.d=37.(b+d).
A táblázat első oszlopa alapján
40,5.a+35,5.b=39,5.(a+b).
A táblázat második oszlopa alapján
45.c+38.d=x.(c+d),
vagyis 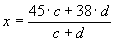 .
.
Az első három egyenletet rendezve 3c = 1,5a, vagyis 2c =a; d = 1,5b; a = 4b, vagyis b = 0,25a.
A d kifejezhető c segítségével (ez azért jó, mert így a 4. egyenletben csak c fog szerepelni, ha behelyettesítünk):
d=1,5b=1,5.0,25.a=1,5.0,25.2c=0,75c.
Ezt beírjuk a negyedik egyenletbe, majd c-vel egyszerűsítünk:
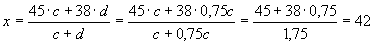 .
.
A két osztályban az összes lány átlagpontszáma a számításaink szerint 42.
14. Legyen a hat szám a\(\displaystyle le\)b\(\displaystyle le\)c\(\displaystyle le\)d\(\displaystyle le\)e\(\displaystyle le\)f. Mivel a medián 5, ezért c\(\displaystyle le\)5 és 5\(\displaystyle le\)d.
Három eset lehetséges:
Ha 5\(\displaystyle le\)d<6, akkor a sorrend a, b, c, d,... Vagyis a medián d.
Ha d = 6, akkor a sorrend a, b, c, d, 6, e, f. Vagyis a medián d, ami 6-tal egyenlő.
Ha 6 < d, akkor a sorrend a, b, c, 6, d, e, f. Vagyis a medián 6.
Így elmondható, hogy ha a hat számhoz hozzávesszük a 6-ot is, akkor a hat számnak a
mediánja az [5; 6] intervallumban lesz.
15. A szórás kiszámításához szükségünk van az átlagra.
András átlaga 4, Bálint átlaga 3,8, végül Csaba átlaga 3.
Használjuk a megismert képletet!
András jegyeinek szórása 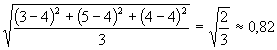 .
.
Bálint jegyeinek szórása 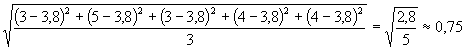 .
.
Csaba jegyeinek szórása 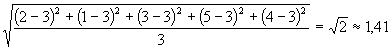 .
.
Most részletesen kiírtuk a képletbe behelyettesítést, természetesen nagyobb minta esetén ezt nem tesszük meg. A zsebszámológépek statisztikai funkciói között megtalálható a szórás kiszámítása is. Ez lényegesen gyorsítja a számításainkat.
16. Az első adatsor átlaga 4,9, a másodiké pedig 8,9.
Használjuk az átlagos abszolút eltérésre megismert képletet!
Az elsőé:
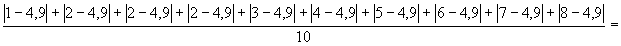
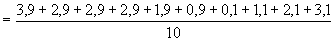 .
.
A másodiké:
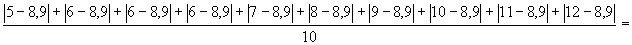
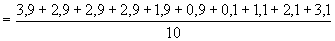 .
.
Jól látható, hogy a két adatsornak egyenlő az (átlagtól vett) átlagos abszolút eltérése. Általában is bizonyítható lenne, hogy ha az adatsor minden elemét ugyanannyival növeljük, akkor az átlaga is ugyanannyival nő, az (átlagtól vett) átlagos abszolút eltérése viszont nem változik.
17. Az abszolútérték-függvények ábrázolásánál tanultak alapján a g(x)=|a-x|+|b-x| hozzárendelésű függvény képe a következő alakú lesz:
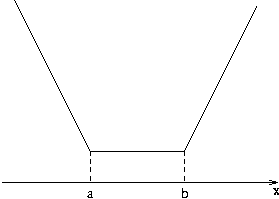
Legyenek a magasságok: x1\(\displaystyle le\)x2\(\displaystyle le\)x3\(\displaystyle le\)x4\(\displaystyle le\)x5. Vázlatosan megrajzolhatjuk a g1(x)=|x1-x|+|x5-x|, g2(x)=|x2-x|+|x4-x|, g3(x)=|x3-x| hozzárendelésű függvények képét egy koordinátarendszerben.
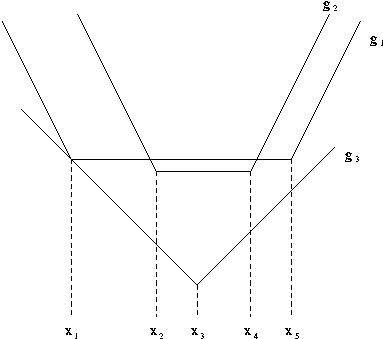
Végezzük el gondolatban a grafikus összeadást, az x3-nál lesz a függvény minimum helye.
Észrevehető, hogy az x3 pontosan az x1;x2;x3;x4;x5számsokaságnak a mediánja.
Így általánosságban is megmutathatnánk, hogy az átlagos abszolút eltérés a mediántól
a legkisebb. Ezért nevezzük az Sn(medián) számot a sokaság átlagos minimális eltérésének.
18. Az f(x) másodfokú függvény. A másodfokú, ax2+bx+c alakú függvények
vizsgálatakor tapasztalhattuk, hogy 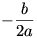 -nál van a minimum helyük.
-nál van a minimum helyük.
Végezzük el a következő átalakítást:
(x1-x)2+(x2-x)2+(x3-x)2+(x4-x)2=4x2-2(x1+x2+x3+x4)x+x12+x22+x32+x42.
A feladatban szereplő másodfokú függvénynek a minimum helye
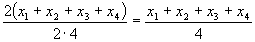 .
.
Észrevehető, hogy ez pontosan az x1;x2;x3;x4 számsokaságnak a számtani közepe. Hasonló módon mutathatnánk meg általánosságban is, hogy a számsokaság átlagától vett átlagos négyzetes eltérés lesz a minimális.
19. A tanult definíciók felhasználásával a következő eredményekhez jutunk:
a) Az osztály átlaga 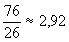 .
.
b) A lányok átlaga 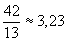 , a fiúk átlaga:
, a fiúk átlaga: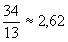 .
.
c) Az osztályra vonatkoztatott medián 3.
d) Medián a lányok és a fiúk esetén is 3.
e) Az osztályra vonatkoztatott módusz 4. (Összesen nyolcan írtak négyes dolgozatot.)
f) Módusz a lányok és a fiúk esetén is 4.
e) A lehetséges érvelések, ezek jó fantáziával folytathatók:
A lányok szerepeltek jobban: "Az átlaguk magasabb, mint a fiúké, és több ötös dolgozattal rendelkeznek."
A fiúk összessségében nem rosszabbak: "A mediánjuk és a móduszuk is egyezik a lányokéval. Az átlagnál van egy kis eltérés, de kerekítve a lányoké és a fiúké is 3."
Nem lett rossz ez a dolgozat: "Az osztályra vonatkoztatott módusz 4, az osztályban 10 tanuló (az osztálynak majdnem a fele) négyes vagy ötös dolgozatot írt."
Az eredmény csapnivaló: "Az osztályban 10 tanuló (az osztálynak majdnem a fele) egyes vagy kettes dolgozatot írt. Az osztály átlaga nem éri el a 3-at sem."
20. Csak elkezdjük, mindenki folytathatja.
a) Sándor beszéde: "A számok magukért beszélnek! A tantestületből 19-en tettek az első helyre. Ilyen magas eredményt senki nem ért el a jelöltek közül. A testület akarata egyértelmű. Győztesként mondok köszönetet..."
b) József beszéde: "Az első helyen leadott szavazatok a legértékesebbek, de ne felejtsük el a második és a harmadik helyeket is összeszámolni. Úgy igazságos, ha az első helyek 3, a második helyek 2 a harmadik helyek pedig 1 pontot érnek. Rövid számolás után a számok valóban magukért beszélnek! A 102 ponttal a testület egyértelműen kifejezte akaratát. Most már győztesként mondhatok köszönetet..."
c) Benedek beszéde: "Ne felejtsük el, hogy a tantestület 48 fős. Bármilyen számításokat elvégezhetünk, mindenki láthatja, hogy a testület nem tudott választani. Egyik jelölt sem tudott meggyőző fölényre szert tenni, mindegyik jelölt a testület kb. harmadának bizalmát élvezi. Így nem lehet irányítani egy iskolát. Javaslatom szerint meg kell ismernünk még alaposabban a jelöltek pályázatát, elképzeléseiket a jövőről, majd új szavazást kell tartanunk..."
21. A menetrend tanulmányozása után a következő válaszokat adhatjuk a feltett kérdésekre:
a) A nap első járata 4 óra 14 perckor, az utolsó 23 óra 34 perckor van ebben a megállóban.
b) Legtöbbet, 28 percet kell várakoznunk 22 óra 54 perctől 23 óra 22 percig.
c) A legrövidebb követési idő 5 perc.
d) Egy nap 134 járat van.
e) 3 óra 44 perctől 23 óra 34 percig bármikor érkezhetünk a megállóba. Ebben az időben fél
óránál kevesebbet kell várakoznunk. Ez összesen 19 óra 50 perc, vagyis 1190 perc a nap 24
órájából (1440 percéből).
Ez a nap 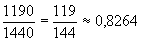 -ed része, vagyis a nap 82,64 %-ában mondható, hogy nem kell
fél óránál többet várakozni a megállóban.
-ed része, vagyis a nap 82,64 %-ában mondható, hogy nem kell
fél óránál többet várakozni a megállóban.
f) Minden járat előtt van 5 perc, amikor elmondhatjuk, hogy biztosan nem kell 5 percnél többet
várakozni a megállóban. Vagyis egész nap összesen 134.5=670
ilyen perc van.
Ez a nap 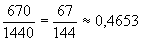 -ed része, vagyis a nap 46,53 %-a.
-ed része, vagyis a nap 46,53 %-a.
g) Ez a reggeli (iskolába, munkába mennek az emberek), és a délutáni nagy forgalommal (hazafelé mennek az emberek) magyarázható.
h) A tanult középértékekre gondolhatunk. Összesen 133 követési idő van egy nap. Ezeket meg tudjuk határozni.
Átlag: 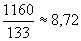 perc.
perc.
Módusz: 6 perc.
Medián: 7 perc.
i) A pontos hétvégi menetrendhez végezhetnénk előtanulmányokat. Megfigyelésekkel, utazási szokásokra vonatkozó kérdőívekkel pontosabb képet nyerhetnénk. Azt azonban így is tudjuk, hogy hétvégén az emberek nem utaznak reggel iskolába, munkába. A járatokat lehet általában ritkábban indítani, mint hétköznap. Napközben érdemes sűríteni valamennyit. Egy lehetséges terv:
|

