A KöMaL 2015. januári fizika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
M-jelű feladatokA beküldési határidő 2015. február 10-én LEJÁRT. |
M. 347. Rögzítsünk hurkapálcát egy asztal szélére! Terheljük fokozatosan a szabad végét, vagy akasszunk rá erőmérőt! Mérjük meg a pálca eltöréséhez szükséges \(\displaystyle M\) forgatónyomatékot, illetve a terhelő erő \(\displaystyle W\) munkáját! Változnak-e a mérési eredmények, ha a hurkapálca asztalon túl kinyúló részének \(\displaystyle \ell\) hosszát a felére csökkentjük?
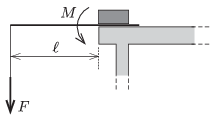
Varga István (1952-2007) feladata
(6 pont)
 |
P-jelű feladatokA beküldési határidő 2015. március 10-én LEJÁRT. |
P. 4693. Hány kelvinen mutat ugyanannyit a higanyos hőmérő Celsius- és Fahrenheit-skálán, és mennyi ez az ugyanannyi?
Közli: Tornyos Tivadar Eörs, Budapest
(3 pont)
P. 4694. \(\displaystyle a)\) Hány gramm víz van egy \(\displaystyle 25~{}^\circ\)C-os, 60 m\(\displaystyle {}^3\) térfogatú szoba levegőjében, ha a relatív páratartalom 50%-os?
\(\displaystyle b)\) Hány százalékra nő a relatív páratartalom, ha a szoba hőmérséklete reggelre \(\displaystyle 20~{}^\circ\)C-ra csökken? (Az ablakok be vannak csukva és jól zárnak.)
\(\displaystyle c)\) Hány százalék ugyanennek a levegőnek a páratartalma \(\displaystyle 10~{}^\circ\)C-on?
Tornyai Sándor fizikaverseny, Hódmezővásárhely
(4 pont)
P. 4695. Egy 5 dioptriás lencsétől 10 cm-re helyezkedik el egy olyan világító, 1 cm hosszú izzószál, amely merőleges az optikai tengelyre. A lencse másik oldalán, ugyancsak az optikai tengelyre merőlegesen helyezünk el egy, a lencse felé forduló síktükröt, tőle 20 cm-re. Hol, mekkora és milyen állású képei keletkeznek az izzószálnak?
Közli: Szombathy Miklós, Eger
(4 pont)
P. 4696. 8 mm átmérőjű és 4 mm magas, henger alakú gyógyszertabletták kis magasságból hullanak az asztalra. Tételezzük fel, hogy minden térbeli irány egyenlő valószínűségű, és a tabletták nem pattannak fel. A tabletták hány százaléka kerül az asztalon ,,gurulós'' helyzetbe?
Bakonyi Gábor (1932-2010) feladata
(4 pont)
P. 4697. Újsághír: ,,Egy elektromos versenyautó három másodperc alatt van százon, maximális sebessége 220 km/h, teljesítménye 268 lóerő.'' Mekkora lehet az autó tömege?
Közli: Radnai Gyula, Budapest
(4 pont)
P. 4698. Egy súlyos vasgolyóhoz \(\displaystyle \ell\) hosszú cérnaszálat, annak végére pedig tollpihét erősítettünk, majd a golyót vízszintes irányban elhajítottuk. A golyó az ábrán látható fémkarikán repül keresztül. Mennyi idő alatt halad át a cérnaszál a karikán?
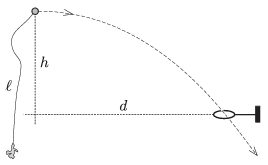
Adatok: \(\displaystyle \ell=\)1,6 m, \(\displaystyle h=\)1,25 m, \(\displaystyle d=2~\)m.
Közli: Holics László, Budapest
(5 pont)
P. 4699. Egy \(\displaystyle \alpha=30^\circ\)-os hajlásszögű lejtőn két vékony lemez egy sínpárt alkot. A lemezek távolsága \(\displaystyle d=1{,}6\) cm. A sínpárra 2 cm átmérőjű golyót helyezünk, és ez csúszás nélkül legördül.
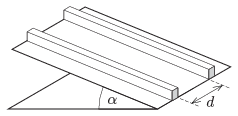
\(\displaystyle a)\) Mekkora a golyó középpontjának a gyorsulása?
\(\displaystyle b)\) \(\displaystyle \mu\) nagyságú súrlódási együttható esetén milyen meredek lejtőnél csúszik meg a golyó?
Vermes Miklós (1905-1990) feladata
(5 pont)
P. 4700. Egy \(\displaystyle h\) magasságú, \(\displaystyle A\) keresztmetszetű (\(\displaystyle h\ll \sqrt{A}\)) homogén fémkorong alkotójával párhuzamosan, nagy gyorsulással mozog (\(\displaystyle a\gg g\)). Hány elektron jelenik meg a fémkorongnak a gyorsulás irányával ellentétes oldalán?
Közli: Honyek Gyula, Budapest
(5 pont)
P. 4701. Függőleges síkban mozgó, szigetelő anyagból készült karika \(\displaystyle P_1\) és \(\displaystyle P_2\) pontjához \(\displaystyle Q\) töltésű, kisméretű golyókat úgy, hogy \(\displaystyle \alpha=60^\circ\) (lásd az ábrát). A karika \(\displaystyle B\) indukciójú, homogén mágneses mezőben van, amelynek erővonalai merőlegesek a karika síkjára. A karikát úgy mozgatjuk, hogy az a szigetelő anyagból készült vízszintes felületen tisztán gördül, és a középpontjának sebessége \(\displaystyle v_0\).
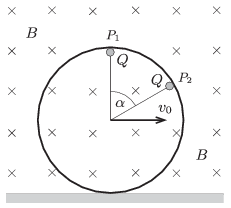
\(\displaystyle a)\) Mekkora mágneses erők hatnak az ábrán látható helyzetben az egyes töltött golyókra?
\(\displaystyle b)\) A karika mely helyzeteiben nincs a mágneses erők eredőjének forgatónyomatéka a karika középpontjára vonatkoztatva? Ezen helyzetek közül melyikben gyakorol nagyobb erőt a mágneses mező a karikára? Mekkora ez az erő?
\(\displaystyle c)\) Határozzuk meg a mágneses erők hatásvonalainak metszéspontját!
Közli: Kotek László, Pécs
(5 pont)
P. 4702. Négy darab 10 cm oldalú, különböző anyagi minőségű betonkockát az ábrának megfelelően helyezünk egymás mellé, és \(\displaystyle {}^{60}\)Co gamma-sugárnyalábbal ,,világítjuk meg'' egymás után 4 pozícióból (S1, S2, S3 és S4). A sugárforrásokkal szemben, a betonkockák mögött 4 detektort is elhelyeztünk (D1, D2, D3 és D4). Az első három mérés szerint a betonkockák a sugárzás intenzitását rendre az eredeti érték 86,76, 71,94 és 84,25 százalékával csökkentik.
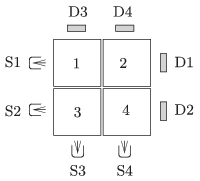
\(\displaystyle a)\) Hány százalékkal csökkent intenzitást mér a negyedik detektor?
\(\displaystyle b)\) Az 1. kocka ,,felezési rétegvastagsága'' 6 cm. Mekkora ez - az anyagi minőségtől függő - mennyiség a többi kockánál?
Közli: Simon Péter, Pécs
(5 pont)
P. 4703. Az ábrán látható alakzatban (amely a közepe felé korlátlanul folytatódik) a fekete körökkel jelzett pontok között \(\displaystyle 1~\Omega\) ellenállású vezetékek vannak.
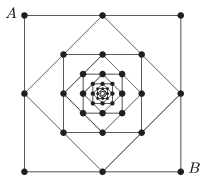
Mekkora az eredő ellenállás az \(\displaystyle A\) és \(\displaystyle B\) pontok között?
Amerikai versenyfeladat nyomán
(6 pont)
A fizika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

