A KöMaL 2015. februári fizika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
M-jelű feladatokA beküldési határidő 2015. március 10-én LEJÁRT. |
M. 348. Egy megterhelt csavarrugónak nemcsak a hossza változik meg, hanem a rugó - ha az egyik vége szabadon elfordulhat - bizonyos mértékig ,,kicsavarodik''. Mérjük meg, hogyan függ a rugó végének szögelfordulása a terhelő erőtől! Végezzünk méréseket különböző menetszámú és különböző erősségű rugókkal!
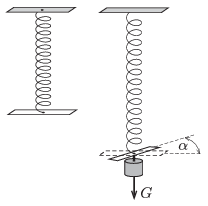
Közli: Gnädig Péter, Vácduka
(6 pont)
 |
P-jelű feladatokA beküldési határidő 2015. március 10-én LEJÁRT. |
P. 4704. Számítsuk ki a higanyos hőmérő gömbjének köbtartalmát \(\displaystyle 0~{}^\circ\)C-nál, ha a \(\displaystyle 0~{}^\circ\)C-os és a \(\displaystyle 100~{}^\circ\)C-os vonalak közötti rész köbtartalma 5 mm\(\displaystyle {}^3\). Az üveg lineáris hőtágulási együtthatója \(\displaystyle 8\cdot 10^{-6}~({1}/{{}^\circ \rm C})\), a higany térfogati hőtágulási együtthatója \(\displaystyle 1{,}8\cdot 10^{-4}~ ({1}/{{}^\circ \rm C})\).
Faragó Andor (1877-1944) feladata
(3 pont)
P. 4705. A Nemzetközi Űrállomás 92 perc alatt kerüli meg a Földet. Tegyük fel, hogy körpályán mozog. Milyen magasan kering a Föld felszíne felett? Mennyit változik naponta a keringési ideje, ha a pályamagassága (két pályakorrekció között) egy nap alatt kb. 100 métert csökken?
Közli: Vass Miklós, Budapest
(4 pont)
P. 4706. Egy 30 cm alapú, rögzített, egyenes lejtő tetejéről súrlódás nélkül lecsúszik egy test. Legalább mennyi idő alatt ér le a lejtő aljára?
Versenyfeladat nyomán
(4 pont)
P. 4707. Vízszintes felületen egy \(\displaystyle m=0{,}2~\)kg és egy \(\displaystyle 4m\) tömegű test súrlódásmentesen mozoghat. A nagyobb tömegű test egy \(\displaystyle D=320~\)N/m rugóállandójú, nyújtatlan húzó-nyomó rugóhoz van erősítve. A kisebb tömegű test \(\displaystyle v_0=5\) m/s sebességgel egyenesen nekiütközik a nyugalomban lévő másik testnek. Az ütközés teljesen rugalmas.
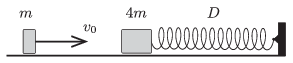
\(\displaystyle a)\) Mekkora a rugó maximális összenyomódása?
\(\displaystyle b)\) Mennyi lesz a rugóhoz erősített test legnagyobb sebessége és a rugó legnagyobb megnyúlása?
Közli: Zsigri Ferenc, Budapest
(4 pont)
P. 4708. Téglalap és négyzet alakú lemezt a síkjukra merőleges és középpontjukon átmenő tengely körül forgatunk. A két lemez tömege, vastagsága és sűrűsége ugyanakkora. A téglalap egyik oldala a másiknak fele. Melyik lemeznek van nagyobb tehetetlenségi nyomatéka? (Nem szükséges a tehetetlenségi nyomatékokat külön kiszámítani!)
Strasser V. Benő (1884-1966) feladata
(4 pont)
P. 4709. Egy 2 dm élhosszúságú, homogén műanyag kocka tömege 1,0 kg, anyagának Young-modulusza \(\displaystyle 10^7~\rm{N/m}^2\).
\(\displaystyle a)\) Mennyire nyomódik össze ez a kocka, ha egy merev, vízszintes lapra helyezzük?
\(\displaystyle b)\) Mennyivel csökken a súlypont magassága?
Közli: Horváth István, Fonyód
(5 pont)
P. 4710. Hőszigetelő edényben lévő 1 kg tömegű, \(\displaystyle 2~{}^\circ\)C hőmérsékletű vízbe annyi \(\displaystyle 0~{}^\circ\)C-os jeget teszünk, hogy a jég éppen elolvadjon, és a víz hőmérséklete \(\displaystyle 0~{}^\circ\)C legyen.
\(\displaystyle a)\) Nő vagy csökken eközben a rendszer entrópiája?
\(\displaystyle b)\) Adjunk számszerű becslést az entrópiaváltozásra!
Varga István (1952-2007) feladata
(5 pont)
P. 4711. Hat egyforma fonálingát készítünk elhanyagolható súlyú, elektromosan szigetelő fonálból és kicsi, 5 g tömegű fémgömbökből. A fonálingák hossza 0,5 m. A hat ingát egyazon pontban felfüggesztjük, majd ezen ponton átmenő függőleges tengely körül megforgatjuk. Elég hosszú idő múlva a kis gömbök vízszintes síkú, \(\displaystyle r\) sugarú körön keringenek.
\(\displaystyle a)\) Mekkora \(\displaystyle r\), ha a keringési idő 1 s?
\(\displaystyle b)\) Mekkora azonos töltéssel kellene ellátnunk a gömböket, hogy forgás nélkül is ugyanezen az \(\displaystyle r\) sugarú körön helyezkedjenek el?
Közli: Légrádi Imre, Sopron
(4 pont)
P. 4712. Egy homogén anyagú, egyenletes keresztmetszetű rézgyűrű mely két pontja közé kapcsolhatunk elektromos feszültségforrást, ha azt szeretnénk elérni, hogy a rézgyűrűben folyó áram keltette mágneses térerősség a gyűrű középpontjában zérus legyen?
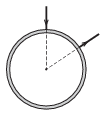
Közli: Radnai Gyula, Budapest
(4 pont)
P. 4713. Függőleges, \(\displaystyle B\) mágneses indukciójú homogén mágneses mezőben lévő fonálon egy \(\displaystyle m\) tömegű, \(\displaystyle Q\) töltésű, kisméretű golyó függ. A golyónak akkora és olyan irányú sebességet adunk, hogy az vízszintes síkban egyenletes körmozgást végezzen. Egy másik alkalommal úgy állítjuk ugyanolyan sugarú, vízszintes síkú körpályára a golyót, hogy az a mágneses mezőben ellentétes irányban körözzön.
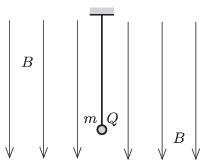
\(\displaystyle a)\) Határozzuk meg a két fonálerő arányát!
\(\displaystyle b)\) Mekkora a szögsebességek nagyságának különbsége a két mozgás során?
Közli: Kotek László, Pécs
(4 pont)
P. 4714. Egy mesterséges hold a Föld körül olyan ellipszispályán kering, amelynek nagytengelye \(\displaystyle 2a\), kistengelye \(\displaystyle 2b\). Határozzuk meg a mesterséges hold sebességét
\(\displaystyle a)\) pályájának a Földhöz legközelebbi pontjában,
\(\displaystyle b)\) pályájának a Földtől legtávolabbi pontjában,
\(\displaystyle c)\) a Föld középpontjától \(\displaystyle r\) távolságban.
Soós Károly (1930-2014) feladata
(5 pont)
A fizika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

