| [69] HoA | 2013-06-18 16:42:43 |
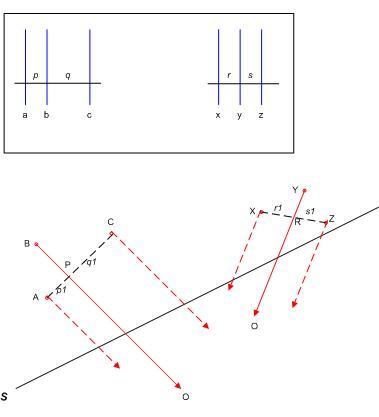
 Az itt következő javaslat egyáltalán nem elméleti. Viszont első közelítésben gyakorlatinak megfelel. Ha feltesszük, hogy a kép elég nagy látószögű és elég részletes, akkor feltehetjük, hogy a bal és jobb oldalán beazonosítható 3-3 , egymástól nem túl távoli, a térképen is jelölt pont. Legyenek ezek a pontok a – szándékosan torzított arányú - ábra szerint a térkép A,B,C ill. X,Y,Z pontjai. S a fénykép síkjával párhuzamos, a térképre merőleges sík. Az S síkban ( az ábra teteje ) a pontoknak megfelelő függőlegesek az ugyanolyan kisbetűvel jelölt vonalak.
Most jön a közelítés: Feltételezzük, hogy A,B,C egymáshoz sokkal közelebb vannak, mint O-hoz, így a belőlük O-ba húzott egyeneseket párhuzamosaknak tekintjük. Ugyanez a helyzet X,Y,Z –re. Ha a fényképen az ab il. bc vonalközök aránya p/q, akkor legyen P az AC szakaszt p1/q1=p/q arányban osztó pont. BP az A,B,C pontokból az O felé mutató irány. Látható, hogy a párhuzamos szelők miatt ezek az egyenesek az S síkon ( annak állásától függetlenül ) is p/q arányú vonaltávolságokat eredményeznek.
Ugyanezt elvégezve az X,Y,Z pontokra, megkapjuk O irányát az utóbbiakból. A két folytonos piros egyenes metszéspontja első közelítésben O helye a térképen.
Az elméleti kérdésre persze nyilván valamilyen kettősviszonyt használó módszert kéne találni.
|
 |
| Előzmény: [68] Hajba Károly, 2013-06-15 22:41:17 |
|
| [68] Hajba Károly | 2013-06-15 22:41:17 |
 Pontosítom az előbbi hsz-m feltételeit:
Adottak az S síkbeli vonalak egymástól való távolságainak arányai (de maga az S sík nem) ill. az A síkbeli pontok és a kettő közötti közvetlen megfelelések.
Milyen feltételek megléte esetén lehet és hogyan megszerkeszteni az O pont helyét?
|
| Előzmény: [67] Hajba Károly, 2013-06-15 22:35:48 |
|
| [67] Hajba Károly | 2013-06-15 22:35:48 |
 Lenne egy elméleti kérdésem, amit érzésem szerint a projektív geometria segítségével lehetne megoldani, ha egyáltalán van megoldás. A kérdésem alapja gyakorlati. Ha létezik megoldás, akkor a munkám során tudnám alkalmazni.
A gyakorlati feladat az, hogy egy régi fénykép alapján keressük meg azt a pontot, ahol az anno készült. Értelemszerűen a régi fénykép egy külső, épületeket ábrázoló kép. Ezen a képen vannak határozott pontok, épületélek, templomcsúcsok, stb-k, melyek beazonosíthatóak egy mai térképen, ha még léteznek.
Vagyis adott egy vízszintes A síkbeli ponthalmaz, melyekre merőleges vonalakat állítok. Adott e halmazon kívül eső O pont és a kettő között egy az A síkra merőleges függőleges S sík, amely nagyjából merőleges a halmaz súlypontja és az O pontot összekötő vonalra is. A halmaz pontjaira állított merőlegeseket a O pontra vetítjük és ezen vetítő síkok egy újabb függőleges vonalat jelölnek ki az S síkon.
Adottak az S síkbeli vonalak ill. az A síkbeli pontok és a kettő közötti közvetlen megfelelések.
Milyen feltételek megléte esetén lehet és hogyan megszerkeszteni az O pont helyét?
Segítségeteket előre is köszönöm.
|
|
| [66] Sinobi | 2013-06-06 18:52:26 |
 Azaz ilyesmi a fordítottja:
Legyen P1,P2,P3,P4 pontok a parabola metszései. Mint az előbb: P1 és P4-ből állított tengelyirányú egyenesek metszései a P1P2 és P3P4 egyenespárral X és Y. Ugyanebből a két pontból a pásik parabola tengelyirányával állított egyenesek metszései X' és Y'. Tudjuk, hogy XY || P2P3 || X'Y' azaz XY párhuzamos X'Y'. Amit be akarunk látni: P1, P4, X és Y egy körön van.
Kidobva a parabolákat a feladatból: Egy metsző x,y egyenespárt elmetszek két párhuzamos egyenessel, kapom X, Y, X', Y' pontokat. Ha P1 és P4 olyan pontok, hogy XP1X' és YP4Y' és YP4Y' derékszög, és P1 y-n és P4 x-en helyezkedik el, akkor P1, P4, X és Y egy körön van. Lásd ábra. derékszög, és P1 y-n és P4 x-en helyezkedik el, akkor P1, P4, X és Y egy körön van. Lásd ábra.
Ennek a bizonyítása: OX/OX' = OY/OY' ahol O az egyenesár metszéspontja, mert YXO és Y'X'O hasonlóak. O-ból egy középpontos nagyítással elérjük, hogy X''O = YO legyen. Ekkor X'''O=Y'O és P1X || P1''X''. x és y szögfelezőjére tükrözve (az egyikre) X'' Y-ba, X''' Y'-be kerül, X''P1'' pedig YP4-be, tehát rakható rájuk kör, tehát P1, P4, X és Y is egy körön van.
|
 |
|
| [65] Sinobi | 2013-06-06 18:04:36 |
 A forítottja egyszerű:
Ha P1,P2,P3,P4 pontok egy húrnégyszögön vannak, és P1P2 és P3P4 egyik szögfelezője sz, akkor sz jó lesz, mint egy parabolának tengelyiránya.
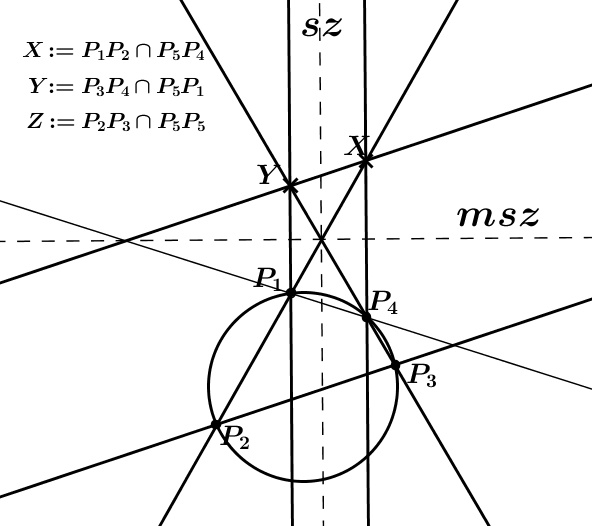
A parabolának az ideális pontja legyen P5, az ott vett érintője az ideális egyenes(?), és a Pascal-tétel értelmében 6 pont (P1,P2,P3,P4,P5,P5) csakkor fekszik egy kúpszeleten, ha a rájuk fektetett egyenesek metszései egy ponton mennek át. Elegendő tehát azt belátnom, hogy XY || P2P3.
Az ábra jelölése szerint: X:=P1P2 P5P4, Y:=P3P4 P5P4, Y:=P3P4 P5P1, Z:=P2P3 P5P1, Z:=P2P3 P5P5. P5P5.
Y képe msz-re való tükrözés után P1, X-é P4 tehát XY antiparallel P1P4 tehát parallel P2P3
msz irányú parabola is fektethető rájuk, tehát fektethető rá merőleges parabola is.
|
 |
| Előzmény: [63] HoA, 2013-06-06 13:09:26 |
|
| [64] Vonka Vilmos Úr | 2013-06-06 15:14:23 |
 Ha P1P3P4P5 húrnégyszög, akkor felírva az O pont körülírt körre vonatkozó hatványát OP1.OP3=OP4.OP5, innen OY2=OP52. Vagyis a lehetséges Y1, Y2 pontok az O középpontú P5-öt tartalmazó körön vannak. Ezért a Thales-tétel miatt Y1P5Y2 derékszög. Viszont Y1P5 illetve Y2P5 határozzák meg a lehetséges parabolák ideális pontjait, ami azt jelenti, hogy a lehetséges parabolák tengelyei valóban merőlegesek. A gondolatmenetben minden lépés megfordítható, így az állítás megfordítása is igaz.
|
| Előzmény: [63] HoA, 2013-06-06 13:09:26 |
|
| [63] HoA | 2013-06-06 13:09:26 |
 Az eddigiek alapján egy Feladat: Bizonyítsuk, hogy egy húrnégyszög csúcsaira illeszkedő két parabola tegelye merőleges egymásra.
Igaz-e a fordítottja: Ha két, merőleges tengelyű parabola négy pontban metszi egymást, akkor a négy metszéspont egy körön van ?
|
| Előzmény: [53] jonas, 2013-04-15 10:06:55 |
|
| [62] HoA | 2013-06-05 11:09:16 |
 Szerkesztési feladatnak tekintve 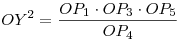 -ből: Legyen Z az OP4(=OP5) egyenes azon pontja, melyre -ből: Legyen Z az OP4(=OP5) egyenes azon pontja, melyre 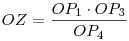 . Ekkor OY2=OZ.OP5 . Ekkor OY2=OZ.OP5
A P1 , P3 , P4 pontokon át rajzolt kör kimetszi OP5 -ből Z-t, OY megegyezik a ZP5 szakaszt húrként tartalmazó körhöz O-ból húzott érintő hosszával.
|
| Előzmény: [59] Vonka Vilmos Úr, 2013-06-03 16:27:11 |
|
|
|
| [59] Vonka Vilmos Úr | 2013-06-03 16:27:11 |
 Ha végiggondoljuk, hogy mi a hiba a bizonyításban, akkor ezzel a gondolatmenettel is kaphatunk egy indoklást az eredeti kérdésre.
Ugyanis olyan P2 ideális pontot kell keresnünk, amelyre teljesül, hogy a P1, P2, P3, P4, P5 pontokra illeszkedő kúpszelet parabola. Ez éppen akkor teljesül, ha a P2 pontbeli érintő az ideális egyenes. A P2 pontbeli érintőt a Pascal-tétel segítségével szerkesztve (a P2P1P3P4P5P2 hatszöget használva) azt kapjuk, hogy ez pontosan akkor áll fenn, ha az X=P1P2 P4P5 és Y=P2P5 P4P5 és Y=P2P5 P1P3 pontok egyenesre párhuzamos P3P4-el. P1P3 pontok egyenesre párhuzamos P3P4-el.
Legyen O=P1P3 P4P5 (és tegyük most fel az egyszerűség kedvéért, hogy ez nem ideális pont). A keletkező háromszögek hasonlósága alapján (és felhasználva a négyszög konvexitását, ami miatt O az oldalszakaszokon kívül esik) P4P5 (és tegyük most fel az egyszerűség kedvéért, hogy ez nem ideális pont). A keletkező háromszögek hasonlósága alapján (és felhasználva a négyszög konvexitását, ami miatt O az oldalszakaszokon kívül esik) 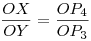 és és 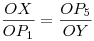 ; ahonnan ; ahonnan 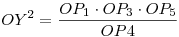 . A P1, P3, P4, P5 pontok a négyszög rögzített csúcsai, ezekhez két olyan Y pont van, amire a fenti egyenlőség teljesül. Ebből következően két olyan P2 ideális pont létezik, ami eleget tesz a feltételeknek. . A P1, P3, P4, P5 pontok a négyszög rögzített csúcsai, ezekhez két olyan Y pont van, amire a fenti egyenlőség teljesül. Ebből következően két olyan P2 ideális pont létezik, ami eleget tesz a feltételeknek.
Ezt a dolgot egyébként a legegyszerűbben Desargues ivolúciótételét felhasználva lehet belátni, de azt gondolom, hogy az a gondolatmenet nem "elemi", ezért nem teljesen idevaló.
|
| Előzmény: [57] HoA, 2013-06-02 22:12:27 |
|
| [58] jonas | 2013-06-03 12:13:53 |
 Ezt Pascal-tétel nélkül is el lehet mondani.
Legyenek a négyszög csúcsainak koordinátái (x1,y1),(x3,y3),(x4,y4),(x5,y5). Legyen a tengely irányvektora (x2,y2). Ekkor az ismert képlet szerint a négy ponton átmenő és a tengely irányú parabola pontjai azok az (x6,y6) pontok, ahol
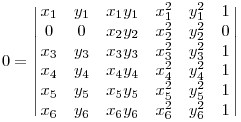
Persze ez ugyanúgy hibás, mint a te szerkesztésed.
|
| Előzmény: [57] HoA, 2013-06-02 22:12:27 |
|
| [57] HoA | 2013-06-02 22:12:27 |
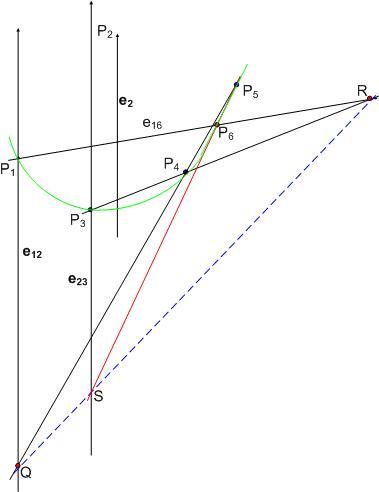
 Erről jut eszembe a következő "bizonyítás". Hol a hiba benne? ( Aki ismeri, ne lője le! )
A síkban bármely konvex négyszög négy csúcsára illeszthető tetszőleges tengely irányú parabola. A Pascal-tétel alapján a parabola további pontjai szerkeszthetők.
Legyenek a négyszög csúcsai P1,P3,P4,P5 , az e2 egyenes a tengely iránya. A P1 -en át felvett tetszőleges e16 egyenes és a parabola P6 metszéspontjának szerkesztése: Legyen P2 a parabola ideális pontja. Ekkor P1P2 ( e12 ) a P1 -en át húzott e2vel párhuzamos egyenes, ennek P4P5 -tel alkotott metszéspontja legyen Q. P2P3 ( e23 ) a P3 -n át húzott e2vel párhuzamos egyenes, ennek P5P6-tal vett (egyelőre ismeretlen ) metszéspontja S. A P3P4 és a P6P1=e16 egyenes metszéspontja R. S-et megkapjuk mint QR és e23 metszéspontját, P6 így P5S és e16 metszéspontjaként adódik.
|
 |
| Előzmény: [53] jonas, 2013-04-15 10:06:55 |
|
| [56] Fálesz Mihály | 2013-05-29 10:48:04 |
 Ez nem projektív, hanem inkább gömbi/hiperbolikus geometriai kérdés.
A gömbön kétféle, oldalakra és szögekre vonatkozó koszinusztétel is van, ezek valóban egymás természetes duálisai. (A megfelelő képletetek hiperboliklusban is igazak, de nem annyira látványos a dualitás.)
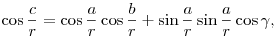
illetve
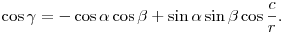
Ezekből úgy kaphatunk euklideszi tételeket, ha átrendezzük, r2-tel megszorozzuk, és vesszük a r  határátmenetet. Úgy képzelhetjük el, hogy az euklideszi háromszöget egy nagy gömbre vetítjük, ami a háromszögünk közelében érinti a síkot, felírjuk a vetület-gömbháromszögre a megfelelő képletet, aztán felfújjuk a gömböt végtelen nagyra. határátmenetet. Úgy képzelhetjük el, hogy az euklideszi háromszöget egy nagy gömbre vetítjük, ami a háromszögünk közelében érinti a síkot, felírjuk a vetület-gömbháromszögre a megfelelő képletet, aztán felfújjuk a gömböt végtelen nagyra.
Az oldalakra vonatkozó koszinusztételből a szokásos koszinusztételt kapjuk, ehhez csak a 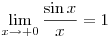 és a és a 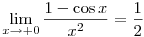 határértékre van szükség. határértékre van szükség.
A szögekre vonatkozó koszinusztétel esetében még egy apró trükk kell: tudnunk kell, hogy a gömbháromszög területe t=r2( + + + + - - ). ).
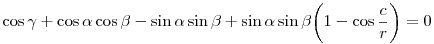
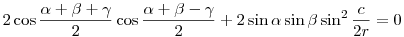
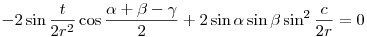
Ha r  , akkor , akkor 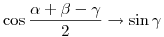 , az euklideszi esetben tehát , az euklideszi esetben tehát
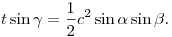
Ha akarjuk, ezt a képletet tekinthetjük a koszinusztétel duálisának.
|
| Előzmény: [54] Sinobi, 2013-05-25 17:00:11 |
|
| [55] Micimackó | 2013-05-28 23:12:42 |
 Nem vagyok biztos benne mire gondolsz, de szerintem (amennyit én a projektív geometriás dualitásról tudok, az alapján) nincs neki. Aztán lehet, hogy a dualitás még jobban kiterjeszthető, nem vagyok a téma szakértője.
|
| Előzmény: [54] Sinobi, 2013-05-25 17:00:11 |
|
| [54] Sinobi | 2013-05-25 17:00:11 |
 mi a cosinus-tétel duálisa?
|
|
| [53] jonas | 2013-04-15 10:06:55 |
 Egyszerű bizonyítást szeretnék a következő tételre.
A síkban bármely konvex négyszög négy csúcsára pontosan két parabola illeszkedik, feltéve, hogy a párhuzamos egyenespárokat is elfajult parabolának számítjuk.
|
|
| [49] Vonka Vilmos Úr | 2013-04-03 22:27:14 |
 A válasz igen; az indoklást pedig nagyban befolyásolja az, hogy hogyan értelmezzük a kúpszeleteket illetve milyen eszközökkel bizonyítjuk a rájuk vonatkozó tételeket. (Például igen gyakran a másik témában tárgyalt Steiner-tételt tekintik a kúpszelet definíciójának, miszerint a kúpszeletek definíció szerint a projektív sugársorok metszési alakzatai. Más tárgyalásban a kúpszeletek definíció szerint a körök kollineációs képei - ekkor nyilván nincs mit bizonyítani.) Tegyük fel, hogy most a kúpszelet fogalmát a középiskolában megismert módon értelmeztük (tehát definíció szerint a kúpszeletek a körökm, az ellipszisek a hiperbolák és a parabolák).
Geometriai módon megkonstruálhatunk például olyan kollineációt, amely tetszőleges kúpszeletet körbe visz át; lényegében azzal a módszerrel, ahogyan a [41] hozzászólásomban megadtam a két kör közötti kollineációt. Egy tetszőleges k kúpszeletet tekintve kiválaszthatunk annak két érintőjét, és ezek közé az érintők közé egy tetszőleges k' kört beírva a k kúpszelet átvihető a k' körbe olyan kollineációval, amelynek centruma a két tekintett érintő metszéspontja. A módszer indoklásánál azonban felhasználtuk, hogy egy kúpszeletet öt "megfelelő adat" egyértelműen meghatároz. Ennek a belátásánál pedig előfordulhat, hogy már kihasználtuk a bizonyítandót. (Ha például ezt a Pascal-tétel segítségével bizonyítottuk, és a Pascal tételt először körre igazoltuk, majd onnan kollineáció alkalmazásával általánosítottuk kúpszletre.)
A [48] hozzászólásodban szereplő koordinátás módszer is célhoz vezet, ellipszisek esetén rendben van az, amit írtál.
A kollineációk koordinátás megadásához azonban a projektív síkon érdemes számolnunk, homogén koordinátákkal. Röviden: a projektív sík pontjait (0,0,0)-tól különböző számhármasokkal jellemezhetjük úgy, hogy az (x1,x2,x3) számhármas és tetszőleges k nem 0 valós szám esetén a (kx1,kx2,kx3) számhármas ugyanazt a pontot jelenti. Az (x,y) pontnak az (x,y,1) számhármas (és annak akármilyen skalárszorosa) felel meg, a (v1,v2) irányvektorú egyenesek ideális pontjának pedig a (v1,v2,0) számhármas felel meg. Ekkor igazolható (nehéz tétel!), hogy minden kollineáció valamilyen rögzített aij skalárok esetén az (x1,x2,x3) ponthoz az (a11x1+a12x2+a13x3,a21x1+a22x2+a23x3,a31x1+a32x2+a33x3) pontot rendeli. Ilyen módon a kanonikus alakban felírt parabolához és hiperbolához is megadható az a kollineáció koordinátásan, amelyik azt körbe transzformálja:
-az 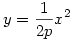 parabola egyenlete homogén koordinátákkal x12-2px2x3=0, ezt a görbét az (x1,x2,x3) ponthoz parabola egyenlete homogén koordinátákkal x12-2px2x3=0, ezt a görbét az (x1,x2,x3) ponthoz 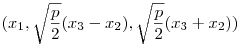 -t rendelő transzformáció az origó középpontú egységkörbe viszi. -t rendelő transzformáció az origó középpontú egységkörbe viszi.
-az 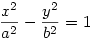 hiperbola egyenlete homogén koordinátákkal b2x12-a2x22-a2b2x32=0, ezt a görbét az (x1,x2,x3) ponthoz az (abx3,ax2,bx1) pontot rendelő kollineáció az origó középpontú egységkörbe viszi. hiperbola egyenlete homogén koordinátákkal b2x12-a2x22-a2b2x32=0, ezt a görbét az (x1,x2,x3) ponthoz az (abx3,ax2,bx1) pontot rendelő kollineáció az origó középpontú egységkörbe viszi.
|
| Előzmény: [47] w, 2013-04-03 21:19:14 |
|
| [48] w | 2013-04-03 21:27:51 |
 Amikor a kérdést először megismertem, a kúpszeletek kanonikus egyenleteire gondoltam: ellipszis esetén
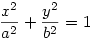 . .
Itt akkor végezzünk két merőleges affinitást, a két tengelyre, úgy, hogy ebből kör-egyenletet kapjunk. Úgy tűnik, a merőleges affinitás kollineáció, hisz az egyenes pontjai esetén kettősviszonytartó, így sugársorokra is ez elmondható.
A kanonikus alak létezése már elemibb dolog, ismert eredmény (tudom, "elkentem").
Az volna a kérdés, hogy ezt parabolákkal, hiperbolákkal meg lehet-e csinálni? Nyilván az ilyesfajta affinitásból ki kellene lépni, vagy sem? (Nem kell az állításaimat komolyan venni :-). )
|
| Előzmény: [47] w, 2013-04-03 21:19:14 |
|
| [47] w | 2013-04-03 21:19:14 |
 Ha már a GEOMETRIA témában felmerült, felvetném:
Van-e minden kúpszelethez olyan kollineáció (kettősviszonytartó transzformáció), amely körbe viszi?
|
|
|
| [45] Sinobi | 2013-03-30 21:53:49 |
 Egy kúpszelet párhuzamosan vetített képe (affinitása) is kúpszelet. Vannak olyan centrális vetítések, amik kúpszeletet kúpszeletbe visznek (triviálisan: a kúp középpontjából történő vetítés mindenképpen kúpszeletbe visz.) Vajon minden centrális vetítés (síkról síkra, a 3-térben) kúpszelettartó-e?
|
|
|
| [43] Sinobi | 2013-03-18 01:49:08 |
 ,,A k2 kört és a hozzá kapcsolódó pontokat H körül kpos hasonlósággal k1-be viszi (enélkül szerintem nem is lehet megoldani)."
Maga Balázs például invertált nagyítás helyett (vázlatosan):
O középponttal k1-re és k2-re a merőleges körök legyenek i1 és i2 (amik tartalmazzák P-t, Q-t, R-t és S-t) H kp-ú k1-t és k2-t kicserélő inverzió P-t R-be viszi, és megtartja i1' k1' merőlegességét, és i1' középpontjának egyenesét (HO), i1' kp-ja tehát O és merőleges k2-re; i1 és i2 egymás képei, tehát Q és S is.
Még csak azt sem kell belátni, hogy a hvonalon van O.
Mondjuk ez elég távol van a projektív geometriától.
|
|
| [42] w | 2013-03-12 19:47:28 |
 Sok a megoldásodban az elméleti háttér.
Én olyan megoldást küldtem be, ami lényegében a Te megoldásod, csak elemi módon van kivitelezve. Vázlatosan:
Lemma. OP=OR, ha H, P, R kollineáris. Biz.: Elvégezzük azt a H középpontú középpontos hasonlóságot, amely k2 kört k1-be viszi. R pont képe olyan R' k1, melyre R' k1, melyre R' HP. R'-ben meghúzzuk a k1-et érintő egyenest, ami a P-ben húzott érintőt O1 pontban metszi, ahol O1P=O1R'. Nyilván HP. R'-ben meghúzzuk a k1-et érintő egyenest, ami a P-ben húzott érintőt O1 pontban metszi, ahol O1P=O1R'. Nyilván 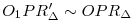 , ahonnan OP=OR is teljesül. , ahonnan OP=OR is teljesül.
Igazoljuk (OQ=OP=OR=OS), hogy QS is áthalad H ponton. A Lemma miatt (HQ k2=X) a k1-et Q-ban és a k2-t X-ben érintő két egyenes metszéspontja (ha létrejön) olyan Y pont, melyre YQ=YX. Ekkor nyilván Y=O, és ezért X=R vagy X=S lehet. Ha viszont X=R, akkor P, Q és R kollineáris, Q k2=X) a k1-et Q-ban és a k2-t X-ben érintő két egyenes metszéspontja (ha létrejön) olyan Y pont, melyre YQ=YX. Ekkor nyilván Y=O, és ezért X=R vagy X=S lehet. Ha viszont X=R, akkor P, Q és R kollineáris, Q P miatt az első bekezdés jelölései mellett Q=R', így O=O1, amiből Q=R és k1=k2 adódik, ez ellentmondás. Tehát mindenképpen X=S. Készen vagyunk. P miatt az első bekezdés jelölései mellett Q=R', így O=O1, amiből Q=R és k1=k2 adódik, ez ellentmondás. Tehát mindenképpen X=S. Készen vagyunk.
* * * * *
Ma hallottam egy másik nagyon szép megoldást. A k2 kört és a hozzá kapcsolódó pontokat H körül kpos hasonlósággal k1-be viszi (enélkül szerintem nem is lehet megoldani). Ezután a P, Q', R, S' pontok által alkotott elfajuló hatszögekre alkalmazhatjuk a Pascal-tételt, ezzel az érintők is könnyen belevihetők. Végül a bizonyítandó állítás adódik a sok kollinearitás miatt.
|
| Előzmény: [41] Vonka Vilmos Úr, 2013-03-12 14:27:02 |
|
